© Song_about_summer/Shutterstock.com
在搜索圖形或樹數據結構時，兩種流行的算法是深度優先搜索 (DFS) 和廣度優先搜索 (BFS)。兩者都用於尋找路徑或遍歷圖的相同目的；然而，DFS 與 BFS 在方法和效率方面有所不同。
DFS是遞歸的，向圖深處遍歷，走到死胡同時回溯，而BFS是迭代訪問所有相鄰節點再向前移動。本文將通過概述主要差異以及與每種方法相關的優缺點來對比 DFS 和 BFS。
DFS 與 BFS:並排比較
DFS vs. BFS:有什麼區別?
乍一看，廣度優先搜索（BFS）和深度優先搜索（ DFS）算法看起來很相似。 BFS 按照樹的寬度遍歷，而 DFS 按照深度遍歷。兩者都有一個共同的目標:搜索圖形以定位單個節點或路徑。因此，下面將進一步討論它們之間的主要區別。
接近和遍歷順序
DFS（深度優先搜索）和 BFS（廣度優先搜索）是兩種廣泛使用的算法用於遍歷圖和樹。兩種算法都訪問圖或樹的每個節點或頂點；但是，它們的遍歷順序和方法各不相同。
DFS 採用深度優先的方法，依次遍歷每個分支，直到到達每個分支的深度。換句話說，它在回溯之前盡可能沿著每個分支探索。 DFS採用的遍歷順序是LIFO（Last In First Out），即使用棧數據結構存儲訪問過的節點。
BFS則採用廣度優先的方式；在繼續訪問更深深度的節點之前，它會訪問當前深度的所有節點。也就是說，它會在進一步向下分析之前分析每個級別的每個節點。此外，它的遍歷順序是FIFO（First In First Out），利用隊列數據結構存儲訪問過的節點。
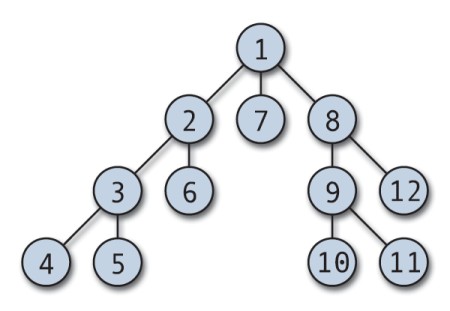DFS 算法會在回溯之前盡可能向下搜索每個分支。
©Wolfram Esser/CC BY-SA 3.0 – 許可證
時間和空間複雜度
DFS 和 BFS 之間的另一個顯著區別是它們的時間和空間複雜度。 DFS 的時間複雜度為 O(V+E)，其中 V 是頂點數，E 是圖或樹中的邊數。此外，它的空間複雜度也超過了 O(V+E)，因為所有訪問過的節點必須存儲在堆棧中，直到到達它們各自的葉子。
相反，BFS 的時間複雜度為 O(V+E) , 類似於 DFS;然而，它的空間複雜度是 O(V)，因為它將所有訪問過的節點存儲在一個數組中。因此，在處理大型圖或樹時，BFS 可能需要比 DFS 更多的內存。
用例和應用
DFS 和 BFS 具有不同的用途和應用。當搜索空間又大又深時，通常會使用 DFS，其目標是在回溯之前探索任何給定路徑。當嘗試在遊戲或謎題中找到解決方案時，它也可能是有益的，因為答案可能位於謎題空間的深處。
另一方面，在搜索大型且淺搜索空間以確定兩個節點或頂點之間的最短路徑。它還確定地理地圖上兩個網絡節點或位置之間的最近距離。
完整性和最優性
搜索算法必須滿足兩個基本要求:完整性和最優性。完備性是指算法是否能保證在存在解的情況下找到解，而最優性是指找到通向該解的最短或最優路徑。
DFS 不是完美的或最優的，因為它可能會陷入困境無限循環或找不到最短路徑。如果其圖形或樹中的循環無法跟踪訪問的節點，DFS 可能會卡住。此外，DFS 可能會找到解決問題的次優路徑。
但是，BFS 是完備且最優的。它保證找到一個解決方案（如果存在），並在其中找到最短路徑。在移動到另一個深度之前探索一個深度級別的所有節點後，BFS 確保它找到最短路徑。儘管如此，在某些情況下，BFS 可能比 DFS 花費更長的時間，尤其是在處理深度或窄圖或樹時。
內存管理
在 DFS 和 BFS 之間進行選擇的另一個關鍵因素是內存管理。內存管理是指算法如何使用內存以及存儲訪問節點需要多少空間。
DFS 使用堆棧來存儲訪問節點，但大的搜索空間或圖可能會導致問題。在這種情況下，DFS 可能會耗盡內存並且無法找到最佳解決方案；由於頻繁的循環，密集的圖或樹需要更多的內存。
BFS 依靠隊列數據結構來存儲訪問過的節點，保證它不會耗盡內存。但是，在某些情況下，BFS 可能會比 DFS 使用更多的內存，尤其是當圖或樹又寬又淺或有很多分支時。如果節點很多或結構稀疏，BFS 也可能需要更多資源。
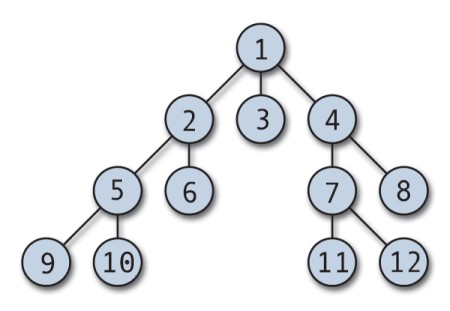BFS 算法在移動到下一個深度的節點之前搜索一個深度的所有節點。
©Alexander Drichel/CC BY-SA 3.0 – 許可證
實現複雜度
算法的實現複雜度是指執行它的難易程度。這取決於所使用的編程語言、可用的數據結構以及成功完成所需的任何邏輯。
DFS 通常比 BFS 更容易實現，因為它只需要一個堆棧數據結構和遞歸函數或循環。 DFS 可以使用一種簡單的深度優先搜索算法來實現，該算法在依次探索每個分支之前訪問每個節點。此外，使用遞歸編程語言（例如 Python）實現起來更簡單，其中遞歸很自然。
BFS，關於另一方面，需要隊列數據結構和循環。為了有效地實現它，BFS 使用廣度優先搜索算法，該算法在移動到下一個深度之前訪問一個深度的所有節點。然而，在像 Python 這樣的遞歸編程語言中實現 BFS 可能更具挑戰性，因為它們需要一個真正的循環而不是簡單的遞歸。
應用
DFS 和 BFS 在各個領域都有不同的應用。 DFS 通常用於計算機圖形學、人工智能和網絡爬行，通過探索 3D 空間來渲染對象來提供 3D 模型和圖像。人工智能將 DFS 用於決策樹或博弈樹——評估每一步可能的移動以探索樹的分支——而網絡爬蟲使用 DFS 來爬網並探索頁面上的鏈接。
BFS 已廣泛應用於網絡路由、最短路徑算法和謎題。在網絡路由中，它通過探索所有可能的路徑直到找到最短的路徑來找到兩個節點之間的最短路徑。 BFS 在最短路徑算法（如 Dijkstra 或 A*）中也發揮作用，保證找到最短路線；類似地，當使用 BFS 解決 Rubik’s Cube 等難題時，您可以確定解決難題的最短解決方案。
使用 BFS 解決魔方將確定解決難題的最快解決方案。
©gd_project/Shutterstock.com
搜索空間
搜索空間是算法可以探索以找到其解決方案的所有可能狀態或配置的集合。它可以表示為圖或樹，其中每個節點代表一個狀態或配置，每條邊表示它們之間的轉換。
DFS 研究搜索空間深度優先的方式，探索每個分支盡可能遠盡可能在回溯和探索其他分支之前。這種方法最適用於解決方案可能深藏其中的大型深度搜索空間。不幸的是，如果存在無限循環並且它不跟踪訪問過的節點，DFS 可能會陷入無限循環。
BFS 以廣度優先的方式遍歷搜索空間，同時探索所有節點在繼續下一步之前的深度。它非常適用於解決方案可能接近根的大型或淺搜索空間。 BFS 保證找到該解決方案的最短路徑，但在某些情況下可能比 DFS 佔用更多內存並且速度更慢。
搜索策略
搜索策略是指決定哪個節點的算法接下來探索。成本、啟發式或隨機性等因素可能會指導此決策過程。
DFS 採用深度優先搜索策略，在返回和探索其他分支之前，它會盡可能地探索每個分支。 DFS 在選擇下一個要探索的節點時不使用任何成本或啟發式方法；因此，它可能會探索次優路徑。在某些情況下，DFS 也可能依賴於隨機性，例如蒙特卡洛樹搜索。
BFS 通常使用廣度優先搜索策略，在繼續下一深度之前探索一個深度的所有節點。相反，它採用統一成本搜索策略，優先考慮成本最低的節點。在某些情況下，BFS 也可能依賴於啟發式算法，例如 A* 算法，它利用成本和估計的距離來決定下一步探索哪個節點。
DFS 與 BFS:10 個必須知道的事實
DFS 代表 Depth First Search，而 BFS 代表 Breadth First Search。DFS 以深度運動的方式遍歷圖或樹，而 BFS 根據樹的寬度移動。為了在 DFS 遍歷期間跟踪訪問過的節點，他們使用堆棧，而對於 BFS，它使用隊列。DFS 可用於拓撲排序、循環檢測和查找圖中的強連通分量；而 BFS 旨在找到兩個節點之間的最短路徑。DFS 佔用的空間更少，而 BFS 需要更多的空間，因為它在進行下一個節點之前將所有節點存儲在當前級別。在解決涉及大量節點的問題時，DFS 速度更快，而 BFS 在處理較小的組時表現出色。DFS 遍歷圖或樹中的所有節點，而 BFS 僅訪問沿最短路徑的節點。DFS 使用深度優先搜索策略，而 BFS 採用廣度優先方法。DFS 可能不會找到最短路徑，而 BFS 總是這樣做。此外，如果您的圖形包含循環，DFS 可能會陷入無限循環；但是，BFS 總是在只剩下有限節點時結束。
DFS 與 BFS:哪個更好?
深度優先搜索 (DFS) 和廣度優先搜索 (BFS) 算法各有優缺點，因此更適合
DFS 以低空間複雜度和基於遞歸的實現有效地遍歷深度圖或無限圖。它還可以有效地檢測圖中的循環，因為它在回溯之前沿著每個分支探索了盡可能遠的距離。 DFS 為尋找連通分量、拓撲排序和 8 字謎等問題提供了解決方案；
相反，BFS 更適合尋找圖中兩個節點之間的最短路徑，因為它會在進入下一層之前檢查該深度的所有節點。此外，它還可以用於計算圖的最小生成樹和解決騎士之旅等問題。
這兩種算法都有自己的時間複雜度，它們之間的選擇取決於特定的問題和正在分析的圖形的特徵。一般來說，BFS 的時間複雜度比 DFS 高，但保證了未加權圖中兩個節點之間的最短路徑；另一方面，DFS 可能具有較低的複雜性，但可能並不總是保證這條最短路徑。
總而言之，DFS 與 BFS 之間的選擇取決於要解決的問題和要分析的圖。兩種算法都有其優點和缺點。因此，了解兩者有助於為特定問題選擇最合適的方法。因此，在您的工具箱中同時擁有這兩種類型的算法以及它們最有益的示例非常重要。
DFS 與 BFS:全面比較和 9 個關鍵差異常見問題解答（常見問題）
h2>
哪種算法更適合尋找兩個節點之間的路徑?
可以使用 BFS 和 DFS 來尋找兩個節點之間的路徑。 BFS 更擅長尋找最短路徑，而 DFS 更喜歡尋找可能不是最短但可能具有其他理想特徵（例如拓撲排序或強連通分量）的路徑。
哪種算法是更適合遍歷稀疏圖?
BFS 在遍歷稀疏圖時更勝一籌，因為它會在繼續之前探索一個級別的所有節點，這使得它在邊很少時效率更高。相反，DFS 可能會探索許多不相關的節點，使其在處理稀疏圖時效率較低。
哪種算法更適合遍歷密集圖?
DFS 在遍歷密集圖時效率更高，因為它會深度探索節點，並且可以快速回溯到仍然與搜索相關的節點。但是，BFS 可能會在到達您想要的節點之前同時探測許多不相關的節點，從而使其在密集網絡中的效率降低。
DFS 和 BFS 可以用於查找圖的連通分量嗎?
是的，DFS 和 BFS 都可以用來發現圖的連通分量。 DFS 從一個節點開始，在返回和探索其他未訪問的節點之前盡可能遍歷，而 BFS 在進入下一個級別之前檢查一個級別的所有節點。
DFS 和 BFS 可以用於檢測圖中的環?
是的，DFS 和 BFS 都可以用來檢測圖中的環。 DFS 通過跟踪列表中的已訪問節點和正在探索的節點堆棧來檢測循環；如果相同的節點再次出現，但沒有以任何順序成為其父節點，那麼它被認為是一個新的循環。類似地，BFS 維護已訪問節點的列表和正在探索的節點的活動隊列；如果先前訪問過的節點在後一個隊列中重新出現但不是它自己的子節點，則它被標記為具有潛在破壞性。
DFS 和 BFS 是否可用於查找有向無環圖的拓撲排序（ DAG)?
是的，DFS 和 BFS 都可以用來確定 DAG 的拓撲排序。使用 DFS，這是通過維護已訪問節點的索引以及正在探索的節點的持續堆棧來完成的。一旦探索了每個節點的所有子節點，就將它們添加到拓撲排序中；類似地，在 BFS 中，還有一個索引跟踪訪問過的節點以及一個等待探索的正在進行的隊列；當一個節點的所有父節點都被探索過後，它也被包含在拓撲排序中。
DFS 和 BFS 可以用來尋找加權圖中的最短路徑嗎?
BFS可以用來尋找未加權圖中的最短路徑，而Dijkstra算法用於加權圖。然而，當權重為非負且搜索僅限於一個連通分量時，DFS 也可能成功。