實際上有兩種實現歸併排序的方法——自上而下的方法和自下而上的方法。現在是簡要概述這些過程的好時機。
自上而下的方法
顧名思義,該算法從初始數組的頂部開始,拆分將數組分成兩半,遞歸地對這些子數組進行排序(即通過拆分它們並重複該過程),然後將結果合併到排序後的數組中。
自下而上的方法
另一方面,自下而上的方法依賴於迭代方法。它以單個元素的數組開始,然後在對它們進行排序時合併兩邊的元素。這些組合和排序的數組被合併和排序,直到只有一個元素留在排序的數組中。主要區別在於,自上而下的方法遞歸地對每個子數組進行排序,而自下而上的方法將數組分解為單個數組。然後,迭代地對每個數組進行排序和合併。
合併排序的工作
在此之後,一個如何使用合併排序的工作示例將很有用。
假設我們有一個數組,arr。 Arr=[37, 25, 42, 2, 7, 89, 14].
首先,我們檢查數組的左索引是否小於右索引。如果為真,則計算中點。這等於“(start_index” + (“end_index”-1))/2,在本例中為 3。因此,索引 3 處的元素是中點,即 2。
這樣,這個7個元素的數組就被拆分成了左右子數組大小分別為4和3的兩個數組:
Left array=[37, 25, 42, 2]
Left array=[37, 25, 42, 2]
右數組=[7, 89, 14]
我們繼續再次計算中點,並將數組一分為二,直到不能再分割為止。最終的結果是:
[37], [25], [42], [2], [7], [89], [14]
然後,我們可以開始合併和排序這些子數組:
[25, 37], [2, 42], [7,89], [14]
然後合併這些子數組並再次排序得到:
[2, 25, 37, 45] 和 [7, 14, 89]
最後,這些子數組被合併排序,得到最終的排序結果array:
[2, 7, 14, 25, 37, 45, 89]
歸併排序的實現
到目前為止,我們已經介紹瞭如何合併排序算法的工作原理、所涉及的步驟以及其背後的工作原理。所以,終於到了看如何使用代碼實現這個算法的時候了。出於說明目的,我們將使用 Python 編程語言。這個過程可以用下面的代碼來描述:
def mergeSort(arr): if len(arr) > 1: mid=len(arr)//2 L=arr[:mid] R=arr[mid: ] mergeSort(L) mergeSort(R) i=j=k=0 while i len(L) and j len(R): 如果 L[i]=R[j]: arr[k]=L[i] i +=1 否則:arr[k]=R[i] j +=1 k +=1 while i len(L): arr[k]=L[i] i +=1 k +=1 while j len( R): arr[k]=R[j] j +=1 k +=1 def printList(arr): for i in range(len(arr)): print(arr[i], end=””) 打印() if__name__==’__main__’: arr=12, 11, 13, 5, 6, 7] print(“給定數組是”, end=”\n”) printList(arr) mergeSort(arr) print(“已排序array is”, end=”\n”) printList(arr)
這看起來代碼很多,但是如果我們把它拆開來還是可以管理的。
解釋代碼
首先,我們將函數 mergeSort 定義為數組“arr”的函數。
第一個“if”語句檢查數組的長度是否大於1. 如果是這樣,我們就可以繼續劃分數組了。
然後,我們計算數組的中點,並將其拆分為“L”和“R”兩個子數組。
在L和R上遞歸調用mergeSort函數,將它們劃分,直到每個子數組只包含一個元素。
此時,三個變量被初始化為零=i,j和k。前兩個是正在操作的子數組的開始和結束索引。 “k”是一個變量,用於跟踪數組中的當前位置。
下一部分以“while”語句開始,是算法的主要部分。該算法在 L 和 R 上迭代,比較 i 和 j 處的元素並將較小的元素複製到數組。與 k 一起,這些索引變量按照增量運算符“=-”遞增。
“while”語句的下一部分指示將兩個數組中的任何剩餘元素複製到初始數組.
我們快完成了。接下來,我們將 printlist 函數定義為數組“arr”的函數。
最後,我們使用“if_name_==’_main_’”行來確保代碼僅在腳本運行時執行直接運行,而不是在導入時運行。
原始數組打印為“給定數組是”,最終排序的數組打印為“排序數組是”。在初始數組按照前面的代碼進行合併排序後,最後一行打印此排序數組。
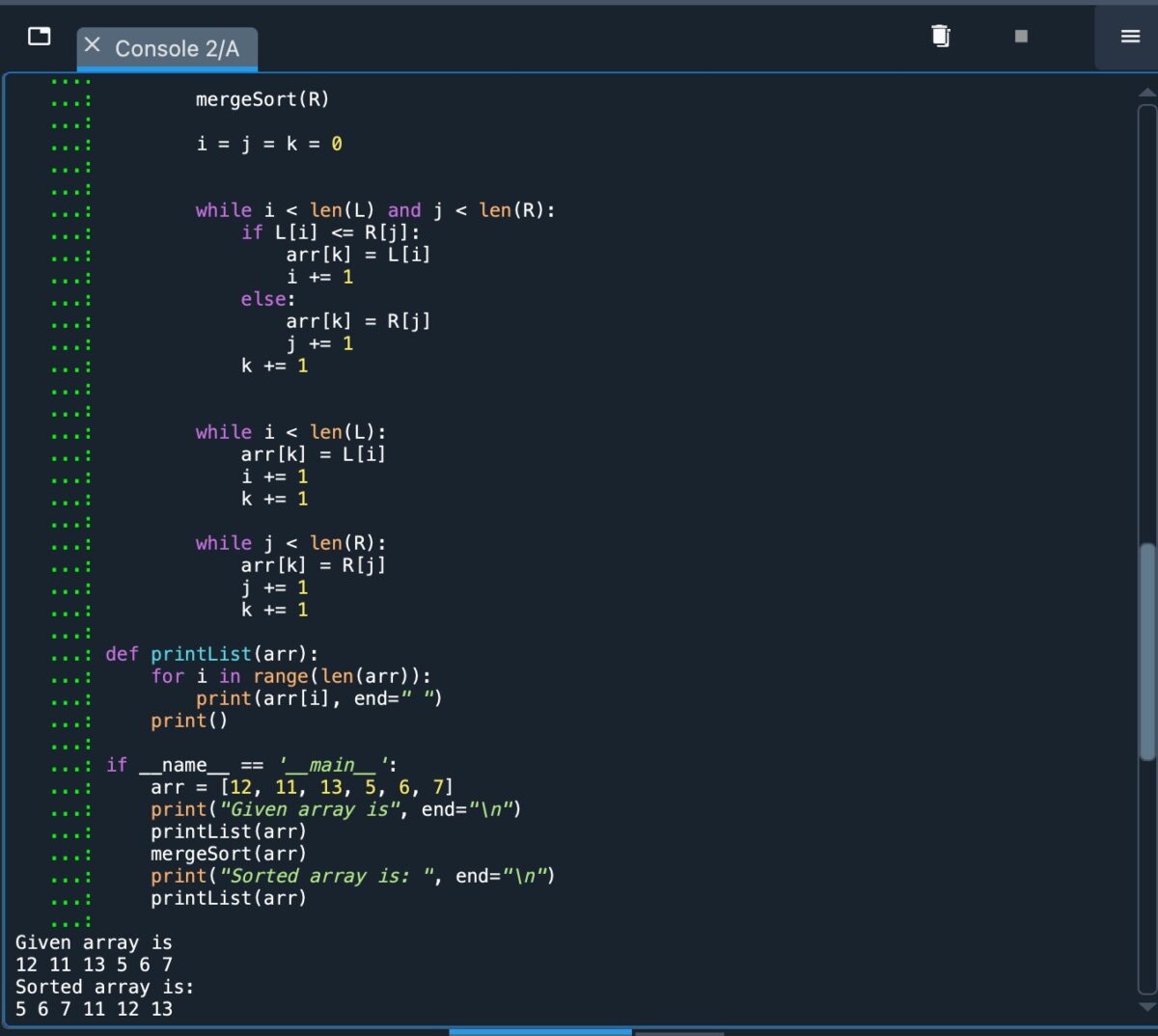
總而言之,下面是顯示此代碼在 Python 中實現的屏幕截圖:
Python 代碼
©”TNGD”.com
插入排序的最佳和最差用例
合併排序是一種簡單的算法,但是,與任何算法一樣, 有最好的用例和最壞的用例。這些在時間複雜度和空間複雜度方面在下面進行了說明。
插入排序的時間複雜度
每種情況下的時間複雜度可以在下表中描述:
最佳情況是指數組部分排序時,平均情況是指數組雜亂時最壞的情況是指數組按升序或降序排列,而你想要相反的順序。因此,這將需要最多的排序。
幸運的是,合併排序在每種情況下都具有相同的時間複雜度,即 O(n log n)。這是因為,在每種情況下,都需要復制和比較每個元素。這導致對輸入大小的對數依賴性,因為數組被遞歸劃分,直到每個子數組包含一個元素。就排序算法而言,合併排序的時間複雜度優於其他一些算法,例如插入排序和選擇排序。因此,歸併排序是處理大型數據集的最佳排序算法之一。
接下來,我們將研究歸併排序的空間複雜度。
歸併排序的空間複雜度
與其他排序算法相比,歸併排序的空間複雜度並沒有那麼好這是因為,合併排序的空間複雜度為 O(n),而不是 O(1) 的複雜度(其中內存使用量是恆定的並且只存儲一個臨時變量),其中 n 是輸入大小。在最壞的情況下,必須創建 n/2 個臨時數組,每個數組的大小為 n/2。這意味著 O(n2/4) 或 O(n2) 的空間需求。但是,在平均和最好的情況下,所需的數組數量是 log(n) base 2,這意味著複雜度與 n 成正比。總的來說,歸併排序的複雜度比較好,算法適用於大型數據集,但內存佔用比其他方法更顯著。
總結
總而言之,已經解釋了合併排序算法的優點和缺點,以及該算法的工作原理,並通過示例進行了說明。歸併排序是一種適用於大型數據集的排序算法,即使它的內存使用率相對較高。簡而言之,這是一種相對容易理解的算法,也是一種可以在許多環境中實施的出色算法。