© whiteMocca/Shutterstock.com
排序算法通常分為兩個陣營——易於實施或運行速度更快。快速排序大多屬於後一類。繼續閱讀以了解如何實現此算法，以及使用它的最佳情況。
什麼是快速排序?
快速排序是一種用於組織數組的排序算法數據。它基本上依賴於稱為分而治之的原則。這是我們將更大、更複雜的問題分解為更簡單的子問題的方法。然後解決這些子問題並將解決方案組合起來找到原始問題的解決方案。
快速排序背後的算法
這不是實現快速排序的確切方法，但給出了它是如何實現的一個想法
//i-> 起始索引，j–> 結束索引 Quicksort(array, i, j) { if (i j) { pIndex=Partition(A, i, j) Quicksor(A,i, pIndex-1) Quicksort(A,pIndex+1, end) } }
首先，我們將快速排序定義為具有起始元素和結束元素的數組的函數。 “if”語句檢查數組中是否有多個元素。
在這種情況下，我們調用“partition”函數，它為我們提供“pivot”元素的索引。這將數組分成兩個子數組，元素分別小於和大於主元。
在每個子數組上遞歸調用該函數，直到每個子數組只有一個元素。然後返回排序後的數組，過程完成。
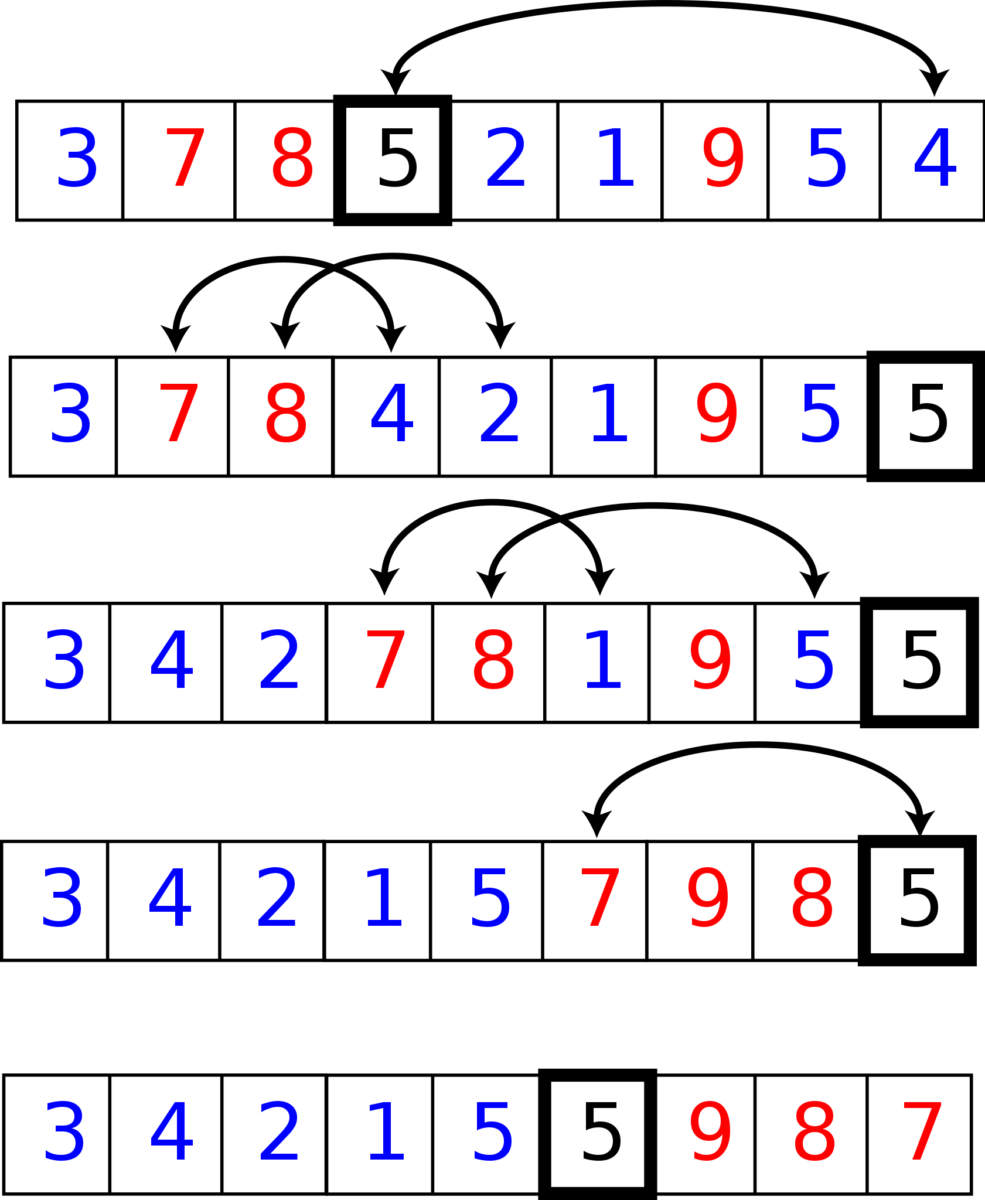在此示例中，帶框的元素是樞軸元素，藍色元素等於或小於，紅色元素大於。
©Dcoetzee/Public Domain – 許可證
快速排序示例
與大多數事情一樣，快速排序最好用一個例子來說明。
讓我們來看下面的數組——[56, 47, 98, 3, 6, 7, 11]
我們有從 0 到 6 的索引（記住第一個元素是索引 0，而不是 1）。
以最後一個元素為基準，重新排列數組，使小於基準的元素在左側，並且較大的元素在右邊。這是通過將 i 和 j 變量初始化為 0 來完成的。如果 arr[j] 或當前元素小於主元，我們將其與 arr[i] 交換並逐步執行此操作。然後將樞軸與 arr[i] 交換，以便該元素處於其排序位置。
這給出了子數組 [6, 7, 3] 和 [56, 47, 98]。樞軸元素的索引現在是 3 而不是 6。
然後調用快速排序，它通過對子數組 [6] 和 [7] 進行排序來圍繞樞軸元素 3 對左側子數組進行排序。
然後我們在右子數組上遞歸調用快速排序，以便將其排序為 [47, 56, 98]。
最後，將子數組組合起來得到排序後的數組 – [3, 6, 7, 11, 47, 56, 98]。
實現
現在我們已經介紹了快速排序背後的基礎，讓我們使用 Python 來實現它。我們使用的代碼可以這樣描述:
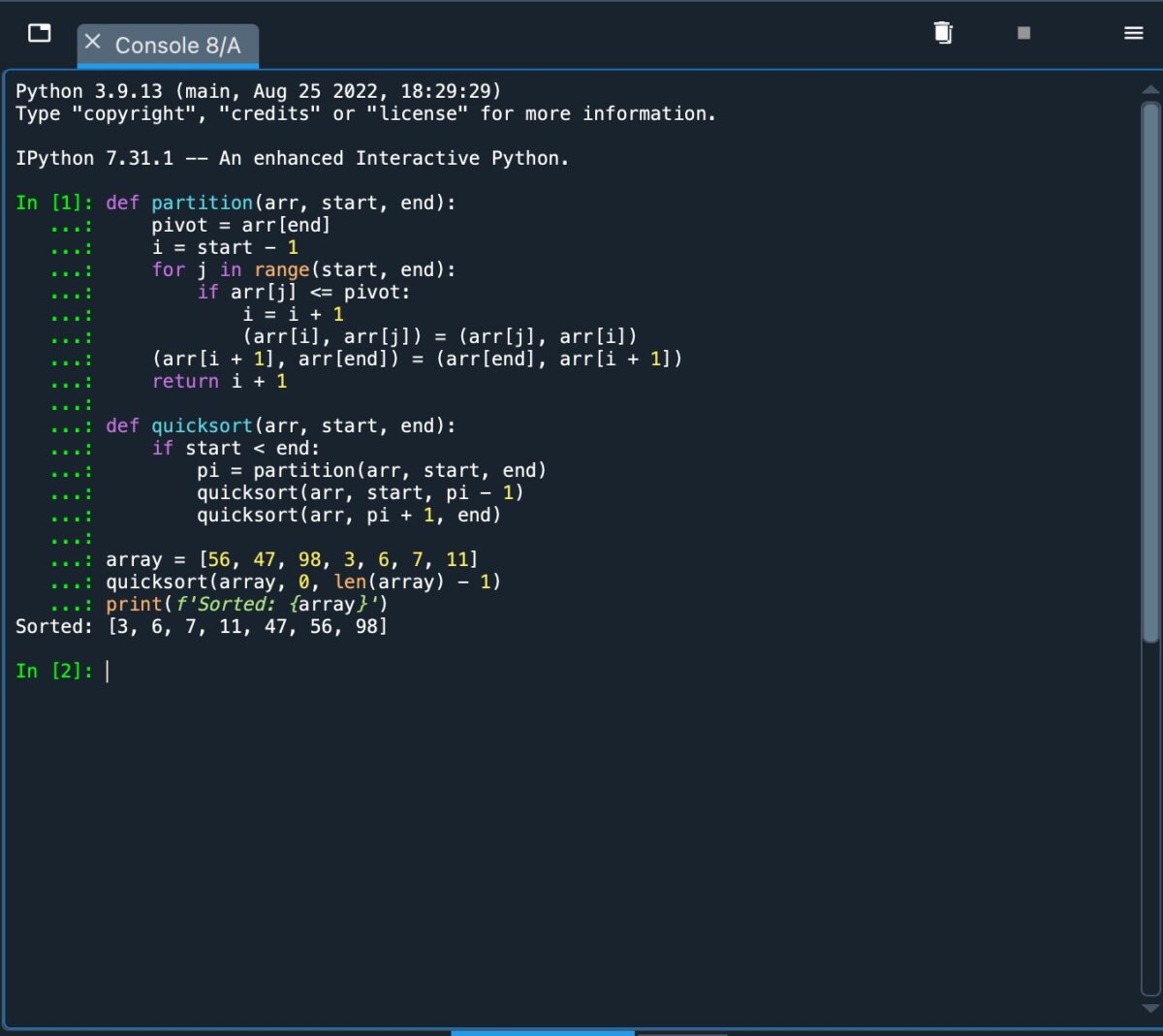
def partition(arr, start, end): pivot=arr[end] i=start-1 for j in range(start, end): if arr[j]=pivot: i=i + 1 (arr[i], arr[j]=(arr[j], arr[i]) (arr[i + 1], arr[end])=(arr[end], arr[i + 1]) 返回 i + 1 def quicksort(arr, start, end): if start end: pi=partition(arr, start, end) quicksort(arr, start, pi-1) quicksort(arr, pi + 1, end) array=[56, 47, 98, 3, 6, 7, 11] quicksort(array, 0, len(array)-1) print(f’Sorted: {array}’)
第一，我們將分區函數定義為數組的函數，具有開始和結束索引。
然後將樞軸值設置為數組的最後一個元素，並將 i 初始化為開始索引，減 1。
“for”循環遍歷數組，從起始索引到結束索引減 1。
“if”語句交換當前元素， j，如果 j 小於或 eq，則為索引 i 處的值正確的樞軸。然後變量 i 遞增。
在此之後，樞軸與索引 i+1 處的元素交換。這意味著樞軸左側的所有元素都小於或等於它，而右邊的元素都大於它。
然後返回樞軸值的索引。
然後將“快速排序”定義為數組的一個函數，並檢查數組以確保它有多個元素。
然後調用“分區”函數，使用索引值設置為“pi”。對左右子數組遞歸調用快速排序，直到每個子數組只包含一個元素。
最後，創建一個排序數組，並使用“print”函數打印出來。
左邊遞歸調用快速排序和右子數組，直到每個子數組只包含一個元素。
©”TNGD”.com
快速排序的最佳和最差用例
雖然快速排序背後的理論可能起初看起來很複雜，該算法有很多優點，而且通常速度很快。我們來看看快速排序的時間複雜度和空間複雜度。
快速排序的時間複雜度
表格總結了快速排序的時間複雜度。
最好的情況是分區平衡時，pivot 接近或等於中值。因此，兩個子數組的大小相似，並且在每個級別執行 n 個操作。這導致對數時間複雜度。
當主元比較接近時，這是平均情況。時間複雜度與最佳情況相同，因為數組的大小大致相等。
但是，最壞情況將時間複雜度變為二次時間。這是因為數組非常不平衡，其中樞軸接近最小或最大元素。這會導致子數組的大小非常不均勻，一個只包含一個元素。因此，有 n 級遞歸和 n 次操作，導致對輸入大小的二次依賴。
快速排序的空間複雜度
另一個要考慮的因素是空間快速排序的複雜性。這可以總結如下:
快速排序的空間複雜度對於最好的和平均的是相同的個案。這是因為該算法具有 log n 個遞歸級別，並且每個遞歸調用使用恆定量的內存空間。因此，總內存空間與遞歸樹的深度成正比。
然而，在最壞的情況下，空間複雜度變為 O(n)。因為遞歸樹明顯不平衡，這意味著有 n 次遞歸調用。
總結
總的來說，顧名思義，快速排序是一種非常有效的排序方式陣列，特別是大的。一旦理解了流程，實施和修改就相對容易了。它在廣泛的場景中都很有用，並為更複雜的排序算法奠定了良好的基礎。
下一個……
什麼是快速排序及其工作原理? (With Examples) FAQs（常見問題）
什麼是快速排序?
快速排序是一種用於對數據數組進行排序的排序算法。它的工作原理是選擇一個樞軸元素，並將數組劃分為兩個子數組，一個元素小於樞軸，一個元素大於樞軸。遞歸地重複此過程，直到每個子數組都已排序並且只包含一個元素。然後將這些數組組合起來得到一個排序數組。
快速排序是一種穩定的算法嗎?
快速排序通常是一種不穩定的算法。這意味著最終輸出中可能不會保留相等元素的相對順序。
快速排序如何選擇基準元素?
您可以選擇第一個或最後一個元素，或進行隨機選擇。對於特別大的數據集，隨機選擇通常會帶來良好的性能。
快速排序的時間複雜度是多少?
最佳和平均情況是O(n log n)，而最壞情況是O(n2)。
快速排序的空間複雜度是多少?
最好的平均情況是 O(log n)，而最壞情況是 O(n)。
使用快速排序的最佳情況是什麼?
快速排序可用於多種數組，但有時，在給定某些約束的情況下，堆排序或歸併排序等替代方法可能效果更好。這通常是您需要像合併排序這樣的穩定算法的地方，或者時間是一個因素的地方。例如，堆排序的最壞情況時間複雜度與快速排序的平均情況時間複雜度一樣好。對於小型數據集，選擇或插入排序等更簡單的算法也可能更快。