© TippaPatt/Shutterstock.com
動態編程 (DP) 是計算機編程的一個要求很高的領域，具有解決問題的特定技能和技巧。是的，如果沒有它，您將成為一名軟件工程師，但動態規劃確實在現實世界中有重要的應用程序，您可能會在開發人員面試中被問及它。
如果您是動態規劃的新手編程或想要更新您的技能，這篇簡短的文章通過示例解釋了什麼是動態編程，以及您可以在何處在線構建 DP 技能。
什麼是動態規劃?
在計算機編程中，動態規劃 (DP) 是一種解決問題的方法，它通過將復雜問題分解為級聯的重疊子問題來構建和簡化複雜問題。通過應用 DP，可以有效地解決多類問題。
DP起源於數學，適用於從生物信息學到水資源工程再到經濟學的各個領域。
動態規劃在計算機科學中是如何工作的?
必須適當地應用動態規劃才能在計算機編程中使用。一個問題必須具有兩個特徵才能適用於 DP:
最優子結構:如果一個特定問題的最優解可以從其子問題的最優解中導出，則該問題具有最優子結構性質。 重疊子問題:所討論的問題應該能夠分解為可重複使用的子問題級聯或可以重複解決子問題而不產生新子問題的遞歸算法。
這兩個屬性是使用 DP 的關鍵。如果使用不重疊的子問題找到最優解，則不能使用 DP。相反，使用分而治之。同樣，歸併排序和快速排序等排序算法也不是DP。
遞歸和動態規劃
遞歸是關鍵DP中使用的最佳子結構的特性。遞歸只是一個自我重複的過程，就像當你站在兩面鏡子之間時，你的倒影會一遍又一遍地重複（Droste 效應）。
最優子結構具有級聯的問題，這些問題不斷地解決自身和遞歸的主要問題。
DP 中的遞歸算法不會產生新的子問題，保持空間量由個別重疊的子問題佔用小。理想情況下，應該一遍又一遍地解決相同的子問題。
動態規劃的主要類型?
動態規劃有兩種類型或方法，具體取決於您處理問題的方式。這兩種方法都使用記憶、存儲和製表解決方案，以便可以快速檢索它們，從而節省了重複計算的時間。
自上而下
在自上而下的方法中，問題的解決方案是遞歸的，允許記憶重疊子問題的解決方案。後續新的子問題通過參考記憶數據緩存來解決，看看是否已經存在解決方案。如果之前未解決子問題，則將其及其解決方案添加到記憶緩存中。
自上而下的 DP 易於理解和使用，因為它有助於有針對性地解決子問題。您可以輕鬆調試它，但這種遞歸方法會耗盡大量緩存內存，從而導致堆棧溢出錯誤。
自下而上
自下而上的方法，也稱為製表或填表，使用製表來創建存儲的子問題和解決方案的記錄。然後，它使用表格化的已解決子問題對問題進行自下而上的重新表述。解決較小的子問題，利用解決方案來解決更大的子問題。 For 循環可用於迭代子問題。
示例:動態編程和fibonacci系列
與斐波那契系列作用時動態編程的實例:
0，1，1，2 , 3, 5, 8, 13, 21, 34, 55…
對於斐波那契數列 (Fn)，序列中的任何數字都是前兩個數字的和。隨著 Fn 中“n”值的增加，計算這些數字的規模和復雜性也會增加。
DP可以用來計算任何斐波那契數。通過使用 DP，您不必生成遞歸樹或一遍又一遍地解決問題。只需使用以前計算的值。以下是代碼如何使用自上而下的方法查找本系列的實現:
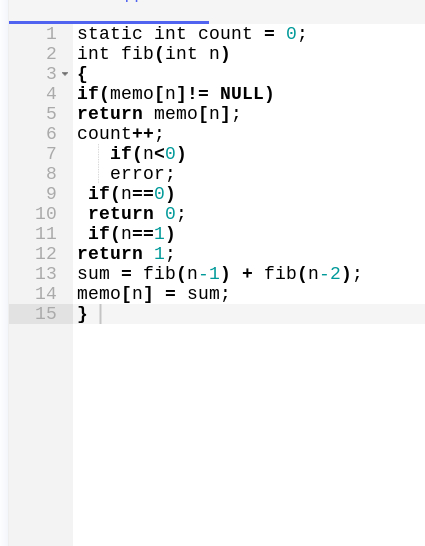計算任意斐波那契數的代碼。
©”TNGD”.com
為什麼動態規劃很重要?
動態編程並不是現代編程領域的重要組成部分。這是因為它通常不直接用於當代生產級開發
儘管它是領先編程語言的一部分，但許多有能力的工程師已經建立了自己，而不僅僅是通過 DP 的知識:
PythonJavaScriptRubyPHPPerlLua
DP 的工作知識對工程師來說很有價值，因為它可以幫助開發人員創建結構更好、效率更高的軟件應用程序。
現代共享服務架構由訪問共享池資源（內存、處理能力、網絡容量、成本）的獨立應用程序組成。結構不良的代碼以及對解決問題的關注不足會導致不必要的資源消耗，從而影響其他應用程序的性能。 DP 有助於改進軟件代碼以防止這種情況發生。
動態規劃的真實示例
有許多使用 DP 保持敏捷和高效並最小化運行它們的系統要求的真實軟件應用程序示例。以下是一些示例:
Google 地圖:在 Google 地圖中，DP 用於識別單個起點和各種目的地之間的最短路徑。搜索引擎:計算兩段在線內容之間的相似度.Plagiarism 軟件:開發文檔距離算法以幫助檢測文本文檔之間的級別相似性。網絡:將數據從單個源順序傳輸到多個不同的接收器。拼寫檢查器:用於量化兩個不同程度的編輯距離算法單詞是併計算將一個單詞更改為另一個單詞所需的操作次數。
數據庫/知識庫緩存:在可訪問的本地內存或緩存中存儲常見查詢/請求。 DP 有助於防止從服務器重複獲取常用數據，有利於本地存儲。
動態規劃面試問題示例
如果您正在尋找下一份軟件工程師或開發人員工作，DP 知識將使您在工作面試中佔據優勢。
DP在技術面試中是一件大事。像谷歌和亞馬遜這樣的領先科技公司經常用必須當場解決的 DP 問題來挑戰候選人！這是為了測試開發人員的思維方式，以及他們是否會分解任務並找到最節省資源的方法來解決問題。
這裡有一些動態編程面試問題和答案的例子
除了上面顯示的斐波那契方程，這裡還有一些常見的動態規劃面試問題，以及示例答案和解決方案:
問題 1:您能解釋一下 Memoization 的優點和缺點嗎?
（提示:這是一個關於 DP 中自上而下方法優缺點的問題）
答案:
memoization 的優點包括:
編碼很容易通過編寫一個自動執行遞歸函數的包裝器或註釋來解決問題答案可以從緩存中獲取並用於多個問題
記憶的主要缺點是如果你有一個很大或很深的數字的計算，您可能會很快耗盡堆棧空間。
問題 2:您正在攀登 st架子。您一次可以爬一級或兩級台階。有多少種不同的方式可以爬到山頂?
（提示:這個問題被稱為“爬樓梯”問題）
答案:看看到達的方法此視頻中的常見編碼面試問題:
在哪裡可以練習動態規劃?
培養動態規劃技能可以增強開發人員的思維能力和解決問題的能力。 DP 還可以幫助您更全面地思考問題並製定不同尋常但有效的解決方案。如果是時候讓您獲得 DP 培訓或認證，這裡有 3 門最好的在線課程:
一旦您掌握了速度，熟能生巧！
四捨五入up
動態編程可能不是您的開發堆棧的一部分，但它對您想為之工作的公司很重要。了解和學習 DP 不僅可以讓你找到工作，還可以提高你的技能，幫助你編寫出你的首席開發人員會喜歡的干淨代碼！
什麼是動態規劃，帶示例常見問題解答（常見問題解答）
什麼是記憶化?
在編程中，記憶化是一種優化技術，將資源密集型函數的結果存儲在緩存中，以便調用它們如果再次需要它們，請快速啟動。這提高了計算機程序的速度和效率。
什麼是製表?
製表是自下而上的動態規劃方法的另一個術語。一個表中填滿了最低級子問題的解決方案，並用於計算更高級別子問題的答案，直到找到原始解決方案。
什麼是分而治之?
分而治之是另一種解決問題的技巧。它將原始問題分解為更小的、相關的、可以獨立解決的子問題。
Google 編碼面試難嗎?
是的。這次虛擬面試享有科技行業最難面試之一的美譽。問題需要廣泛的研究和實踐，通常涵蓋與 Google 服務相關的主題。 DP 問題經常被問到。
Amazon 是否向軟件工程面試候選人詢問有關動態規劃的問題?
是的。亞馬遜從不迴避向應聘者提出高級動態規劃問題，以區分毫無準備的人。