© metamorworks/Shutterstock.com
在對一組數據進行排序時，熟悉排序算法至關重要。在數據結構中，排序是根據數據項之間的線性關係以特定格式排列數據。
排序是必不可少的，因為當數據以給定格式排序時，可以在非常高的級別上優化數據搜索。此外，排序可以以更易讀的格式表示數據。我們有各種各樣的排序算法，但在本文中，我們將研究什麼是堆排序，以及如何使用它。讓我們開始吧！
什麼是堆排序:一個精確的定義
堆排序是一種眾所周知的高效排序算法。這是一個用於對數組數據進行排序的概念，它通過從堆（一個完整的二叉樹）列表的一部分中一個一個地消除元素，然後將它們插入到列表的已排序部分中。
堆排序基本上涉及兩個階段:
使用指定數組的元素創建一個堆，最大堆或最小堆。遞歸地刪除在第一階段構建的堆的根元素。
堆排序算法是如何工作的?
下面是堆排序算法的實現方式:
創建一個最大堆來存儲未排序列表中的數據。從中取出最大值堆並將其插入排序列表。將堆的根與列表中的最後一個元素交換，然後重新平衡堆。一旦最大堆完全為空，返回排序列表。
這是算法
HeapSort(arr)
CreateMaxHeap(arr)
for i=length(arr)到 2
用 arr[i] 交換 arr[1]
heap_size[arr]=heap_size[arr] ? 1
MaxHeapify(arr,1)
結束
讓我們再檢查一下這些步驟。
第 1 步:創建最大值-heap
CreateMaxHeap(arr)
heap_size(arr)=length(arr)
for i=length(arr)/2 to 1
MaxHeapify(arr,i)
End
在這個算法中，我們需要構建一個最大堆。眾所周知，在最大堆中，最大值是根值。每個父節點都需要有一個比其關聯的子節點更大的值。
假設我們有以下未排序值的列表:
[14, 11, 2, 20, 3, 10 , 3]
通過將我們的值放入最大堆數據結構中，這就是我們的列表的樣子:
[20, 11, 14, 2, 10, 5 , 3]
我們可以這樣呈現上面的最大堆:
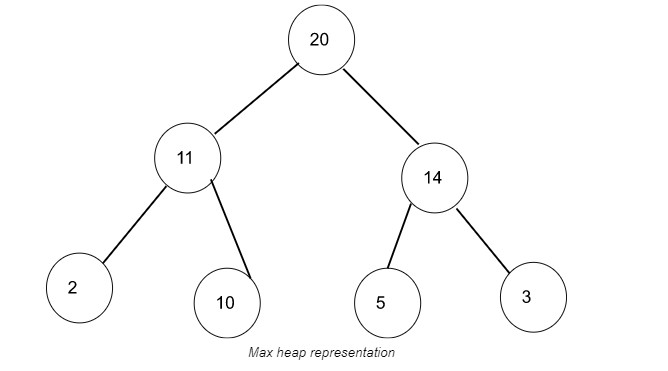最大堆的呈現。
©”TNGD”.com
第二步:取出堆的根
為了對數據進行排序，我們會反復從堆中提取和淘汰最大值，直到為空。如果按照堆的原則，我們可以預見到，最大值會位於堆根。
剔除最大值後，我們不能就這樣拋棄無根堆，因為它將導致兩個節點斷開連接。相反，我們可以將根節點與堆中的最後一個元素交換。由於最後一個元素沒有子元素，因此可以很容易地從堆中移除它。
但是，這一步會導致一個大問題。通過交換這兩個元素，根節點現在不是堆中最大的。堆將需要重組以確保其平衡。
步驟 3:Heapify down（恢復堆）
根值不是較大的值，堆原則已被violated 因為父級的值必須大於子級的值。
但是，這個問題有一個解決方案！我們需要向上堆化，這涉及到向堆的末尾添加一個值，然後沿著數據結構向上移動，直到找到合適的位置。最重要的是，將新的根值與其子值進行比較，選擇具有較大值的子值，並將其與根值交換。沿著堆向下工作，直到它達到平衡。
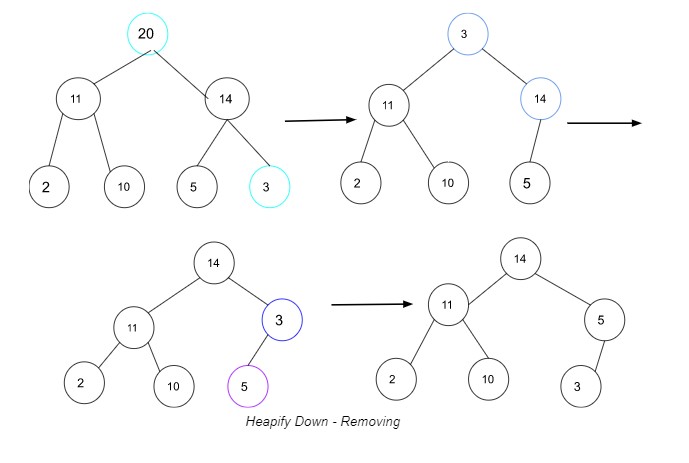heapify down 過程的圖示。
©”TNGD”.com
在上面的示例中，您將原始根值 20 與 3 交換-最右邊的孩子。將 3 作為新的根，將其值與其子值 14 進行比較，因為它大於 3，所以交換它們使 14 成為新的根。接下來，將 3 與其新的子值 5 進行比較，由於 5 大於 3，因此交換它們以使 5 成為新的父值。由於沒有其他孩子可以與 3 進行比較，因此堆現在是平衡的。
第 4 步:重複
您需要重複交換根和最後一個的過程元素，取出最大值，只要數據結構包含大於 1 的大小，就重新平衡堆。滿足此條件時，您將得到一組排序的值。
堆排序複雜性
時間複雜度
這裡是堆排序在最佳情況、平均情況和最壞情況下的時間複雜度。
Best Case Complexity:當數組已經排序時發生，即不需要排序。 O(n log n) 是堆排序的最佳情況時間複雜度。平均情況復雜度:當數組中的元素未按正確的升序或降序排列時發生，導致亂序。 O(n log n) 是堆排序的平均情況時間複雜度。最壞情況復雜度:當您需要以相反順序對數組元素進行排序時會發生這種情況，這意味著如果元素最初是降序的順序，您需要按升序對它們進行排序。 O(n log n) 是堆排序最壞情況下的時間複雜度。
空間複雜度
堆排序的空間複雜度為O(1)
堆排序算法是如何實現的?
Java編程語言是如何實現堆排序的。
//對一個子樹進行堆排序。這裡“i”是arr[]中的根節點索引，“x”是堆大小
public class HeapSort {
public static void sort(int[] arr) {
int x=arr.length;
//重新排列數組（構建堆）
for (int i=x/2 – 1; i >=0; i–)
heapify(arr, x, i);
//從堆中一個一個地提取一個元素
for (int i=x – 1; i > 0; i–) {
//將初始根移動到末尾
int temp=arr[0];
arr[0]=arr[i];
arr[i]=temp;
//在減少的堆上調用 max heapify 函數
heapify(arr, i, 0);
}
}
static void heapify(int[] arr, int x, int i) {
int largest=i;//將最大的初始化為根
int l=2 * i + 1;//左
int r=2 * i + 2;//right
//如果左孩子大於根
if (l x && arr[l] > arr[largest])
最大=l;
//如果右邊的孩子大於目前最大的孩子
if (r x && arr[r] > arr[largest])
largest=r;
//if largest 不是根
if (largest !=i){
int swap=arr[i];
arr[i]=arr[largest];
arr[largest]=swap;
//重複堆化受影響的子樹
heapify(arr, x, largest);
}
}
//打印大小為x的數組的函數
static void printArray(int[]) {
int x=arr.length;
for (int i=0; i x; ++i)
System.out.print(arr[i] + ” “”);
System.out.println();
}
//驅動代碼
public static void main (String[] args) {
int[] arr={ 13, 12, 14, 6, 7, 8 };
排序(arr);
System.out.println(“排序數組是”);
printArray(arr);
}
}
輸出
這是按升序排序的整數數組。
p>
排序後的數組為
6, 7, 8, 12, 13, 14
堆排序算法的優缺點
優點
效率:這種排序算法非常高效，因為對堆進行排序所需的時間呈對數增長，而在其他算法中，隨著排序項的增加，時間呈指數級增長。簡單性:與其他同等效率的算法相比，它更簡單，因為它不使用遞歸等高級計算機科學原理。內存使用:堆排序使用最少的內存來保存要排序的項目的初始列表，並且不需要額外的內存空間即可工作。
缺點
昂貴:堆排序代價高昂。不穩定:堆排序不可靠，因為它可能會重新排列元素的相關順序。低效:在處理高度複雜的數據時，堆排序的效率不是很高。
堆排序的應用
你可能遇到過Dijkstra算法，它使用堆排序來確定最短路徑。在數據結構中，堆排序允許快速檢索最小（最短）或最大（最長）值。它有多種應用，包括確定統計中的順序，管理 Prim 算法（也稱為最小生成樹）中的優先級隊列，以及執行哈夫曼編碼或數據壓縮。
同樣，各種操作系統都使用堆用於作業和進程管理的排序算法，因為它基於優先級隊列。
在現實生活中，堆排序可以應用於 SIM 卡商店，我們有很長的客戶隊列等待服務。可以優先考慮需要支付賬單的客戶，因為他們的工作時間最短。這種方法將為許多客戶節省時間並避免不必要的延誤，從而為所有人帶來更高效和更滿意的體驗。
總結
每種排序或搜索算法都有其優點和缺點，堆排序也不例外。然而，堆排序的缺點相對較小。例如，它不需要超出已分配內存空間的任何額外內存空間。
時間是另一個因素。發現使用nlog(n)確定時間複雜度，但實際堆排序小於O(nlog(n))。這是因為從堆排序中提取會減小大小，從而隨著過程的進行花費更少的時間。因此，出於各種原因，堆排序被廣泛認為是數據結構領域中“最佳”排序算法之一。
什麼是堆排序，如何使用它? FAQs（常見問題）
heapify 是什麼意思?
Heapify 是從二進制的數組表示構建堆數據結構的過程樹。此過程可用於創建最大堆或最小堆。它從二叉樹中非葉子節點的最後一個索引開始，其索引由 n/2 – 1 給出。Heapify 是使用遞歸實現的。
堆排序是如何工作的?
堆排序是一種基於比較的排序算法。它的工作原理是將最大的元素從未排序區域移動到已排序區域，從而縮小未排序區域。堆排序將數組的元素可視化為堆，並且以具有最佳運行時間而著稱。當您想在從數組中提取最小或最大元素時保持順序時，此算法很有用。
如何“堆化”一棵樹?
要重塑或堆化二叉樹，首先選擇一個節點作為子樹的根節點。然後，將根節點的值與其左右子節點的值進行比較。如果任何子節點的值大於（在最大堆的情況下）或小於（在最小堆的情況下）值，則交換根節點和子節點的值較大（或較小）的值。交換值後，遞歸地堆化以子節點為根的子樹，直到整個子樹滿足堆屬性。你對樹中的每個節點重複這個過程，直到整棵樹都滿足堆屬性。
heapify 的時間複雜度是 O(log n)，其中 n 是子樹中被堆化的節點數.
什麼是二叉堆?
二叉堆是一種數據結構，可以認為是一棵完整的二叉樹，其中每個父節點都是小於或等於它的孩子（在最小堆中）或大於或等於它的孩子（在最大堆中）。
堆排序的優點是什麼?
堆排序的優點包括其 O(n log n) 的時間複雜度，它比冒泡排序和插入排序等其他一些流行的排序算法更快。此外，堆排序的內存佔用率低，因為它只需要恆定數量的額外空間。
堆排序的缺點是什麼?
堆排序的缺點包括其不穩定的排序屬性，這意味著排序後可能無法保留相等元素的相對順序。此外，堆排序對於小型數組不是很有效，並且其遞歸性質會導致某些架構上的性能降低。