© BEST-BACKGROUNDS/Shutterstock.com
排序算法是計算機科學中的一個基本概念，用於按特定順序排列數組元素。數據排序在各種應用中都至關重要，從搜索引擎和數據挖掘到科學分析和數據庫。
在選擇使用哪種排序算法時，需要問一些問題:要排序的數據有多大?有多少內存可用?數據會增長嗎?對這些問題的回答可能會決定哪種排序算法最適合每種情況。在選擇排序算法之前，確定您的要求並考慮任何系統限制至關重要。在本指南中，您將了解什麼是排序算法、不同的排序算法以及如何使用它們。讓我們開始吧！
什麼是排序算法?
排序是指以特定格式排列數據。排序算法是一組指令，用於按特定順序排列數組或列表的元素。排序通常採用字典序或數字形式，可以按升序或降序排列。
例如，
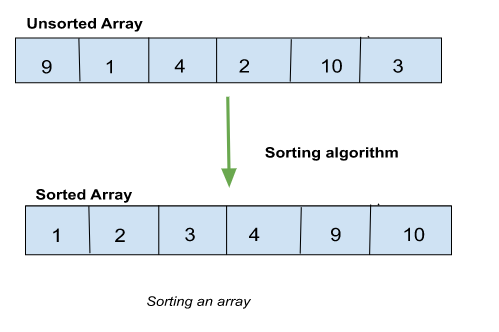按升序排列的數組。
©”TNGD”.com
在上面的例子中，我們是按升序排序。
要完成上面的操作，有多種排序算法可以實現, 可以根據需要使用任何算法。
常用排序算法
選擇排序冒泡排序插入排序歸併排序快速排序堆排序計數排序桶排序基數排序殼牌排序
但是，在我們進入每個排序之前
排序算法的複雜度
任何排序算法的效率通常由空間複雜度和時間複雜度決定
時間複雜度
指算法根據輸入大小完成其執行所花費的時間。它可以用三種不同的形式表示:
Big-O notation (O)Omega notation (Ω) Theta notation (θ)
Space Complexity
This is the total amount of memory an算法需要完整執行。它包括輸入數據和輔助內存。
輔助內存是算法佔用的除了輸入數據之外的額外空間。通常，在確定算法的空間複雜度時會考慮輔助內存。
這裡是不同排序算法的複雜度分析。
排序算法的穩定性
當兩個或多個具有相同值的項目在排序後保持相對位置時，排序算法被稱為
例如，下圖包含兩個相同值為 4 的項目。不穩定的排序算法將允許兩種可能性，其中 4 的兩個位置可能不會保持不變，如下圖所示。
p>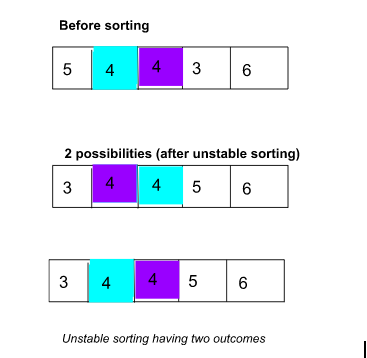 
有兩種可能性排序不穩定
©”TNGD”.com
然而，在穩定排序之後，只有一種可能的結果，即保持位置。看看下面:
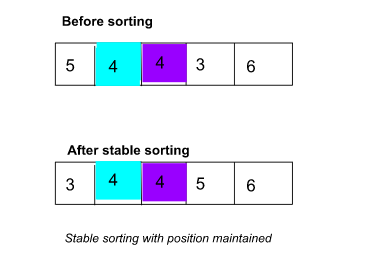穩定排序只有一種可能。
©”TNGD”.com
下表總結了不同排序算法的穩定性。
排序算法如何分類?
您可以根據這些參數對排序算法進行分類:
反轉或交換的次數required:表示算法交換元素以對輸入數據進行排序的重複次數。選擇排序需要最少的交換。比較次數:指算法對元素進行多少次比較以對輸入數據進行排序。是否使用遞歸:一些算法使用遞歸方法對列表進行排序，例如快速排序。此外，其他算法將同時使用遞歸和非遞歸方法對數組元素進行排序。如果它們不穩定 或 穩定:穩定的排序算法保持即使在排序後仍然具有相同值的原始順序，而不穩定的排序算法即使具有相同的值也不會保持元素的相對順序。所需的總額外內存空間:一些算法可以對數據列表進行排序無需創建新列表。這些算法稱為就地排序，需要常量 0(1) 的額外空間進行排序。另一方面，異地排序在排序時會創建新的列表，例如歸併排序。
現在讓我們探索 10 種不同的排序算法，以及如何使用它們。
#1。選擇排序算法
選擇排序是最簡單的排序算法之一，它通過在未排序的列表中找到最小值並將其與第一個元素交換來工作。這個過程一直持續到整個列表被排序。
選擇排序算法是如何工作的?
它是這樣工作的:
從未排序的數組中選擇最少的元素並將其與第一個元素交換。選擇第二個最小元素並將其與列表中的第二個元素交換。從列表中選擇第三個最小元素並將其與列表中的第三個元素交換。重複此過程以找到下一個最小元素並將其放置在正確的位置，直到數組被排序。
選擇排序實現
選擇排序算法可以用多種編程語言實現，例如 Java、Python 和 C/C++。
下面是該算法的實現方式蟒蛇:
在 Python 中實現的選擇排序。
©”TNGD”.com
屬性
空間複雜度 – O(n)時間複雜度 – O(n2)就地排序 – YesStable – No
選擇排序應用
選擇排序在以下情況下使用:
交換成本無關緊要要排序的小列表強制檢查所有元素寫入內存空間的成本很重要
#2。冒泡排序算法
冒泡排序是一種簡單的排序算法，它遍歷一個列表，比較兩個相鄰的值並交換它們直到它們的順序正確。
類似於水中的氣泡如何從底部上升到表面，列表中的每個元素在每次迭代中冒泡到頂部，因此得名氣泡排序。
它具有 O(n^2) 的最壞情況復雜度，使其成為比其他排序算法（如快速排序）更慢的排序算法。然而，冒泡排序的優勢在於它是最簡單的排序算法之一，可以從頭開始理解和編寫代碼。
從技術上講，冒泡排序非常適合對小型數組進行排序或在極其有限的計算機上執行排序算法時內存空間。
冒泡排序如何工作?
讓我們按升序對列表進行排序。
示例:
第一次遍歷列表:
如果我們從列表開始，[3, 1, 5, 2, 8]，算法比較前兩個列表中的元素，3 和 1。因為 3 > 1，它交換它們:[1, 3, 5, 2, 8]現在它比較接下來的兩個值，3 和 5，沒有需要交換 3 5，並且它們是有序的，算法繼續:[1, 3, 5, 2, 8]移動到接下來的兩個值，5 和 2，它們被交換，因為2 5: [1, 3, 2, 5, 8]對於接下來的兩個值，5 和 8，不需要交換，因為它們已經按順序排列:
第二次遍歷列表:
1 3，無需調換位置: [1, 3, 2, 5, 8]算法將交換 3 和 2，因為 2 3: [1, 2, 3, 5, 8]沒有交換，因為3 5: [1, 2, 3, 5, 8]同樣，沒有交換位置，因為兩個值 5 和 8 是按順序排列的:[1, 2, 3, 5 , 8]
現在列表已經排序了，但是算法沒有實現。它將遍歷所有元素而不交換以了解列表是否有序。
第三次遍歷列表:
冒泡排序算法第三遍遍歷列表。
©”TNGD”.com
雖然冒泡排序是一種易於實現的算法，但它的效率不如其他排序算法。
冒泡排序算法是如何實現的?
冒泡排序可以用多種編程語言實現，例如 Python、Java 和 C/C++
這是它在 C++ 中的實現方式:
冒泡排序算法與各種編程語言兼容，例如此處顯示的 C++.
©”TNGD”.com
冒泡排序屬性
空間複雜度 – O(1)最佳案例性能 – O(n)平均案例性能 – O(n*n)Wor st case performance – O(n*n)Stable – Yes
Bubble Sort Algorithm Application
The Bubble sort algorithm is used if:
Complexity don’t matterShort and simple code is preferred
#3。插入排序算法
插入排序是一種簡單的排序算法，涉及將數組中的每個元素插入到其正確位置。它在處理少量元素時使用。
插入排序的工作原理
在這個算法中，我們將關鍵元素與前一個元素進行比較，如果之前的值大於鍵值，那麼我們將之前的值移動到下一個位置。
示例:
從第一個開始輸入列表大小的索引。
[9, 4, 6, 2, 5, 3]
第 1 步:
Key=4//從索引 1 開始
這裡我們將’key’與前面的元素進行比較。
‘key’與9比較，9 > 4，將9移到後面的位置，在前面的位置插入’key’。
結果:[4, 9, 6, 2, 5, 3]
第 2 步:
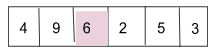比較’key’和之前的元素；在這種情況下，它與 9.
©”TNGD”.com
Key=6//second index
因為 9 > 6，移動 9 到 2nd索引並將 6 插入第一個索引。
結果:[4, 6, 9, 2, 5, 3]
第 3 步:
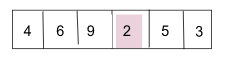將9移動到第二個索引並將 6 插入到第一個索引。
©”TNGD”.com
Key=2//第三個索引
9 > 2 → [4, 6, 2, 9, 5, 3]
6 > 2 → [4 , 2, 6, 9, 5, 3]
4 > 2 → [ 2, 4, 6, 9, 5, 3]
結果:[2, 4, 6, 9, 5, 3]
第四步:
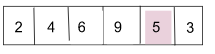從 Key=5//第 4 個索引開始。
©”TNGD”.com
Key=5//第 4 個索引
9 > 5 → [2, 4, 6, 5, 9, 3]
6 > 5 → [2, 4, 5, 6, 9, 3]
4 > 5==!停止
結果:[2, 4, 5, 6, 9, 3]
第5步:
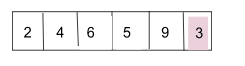接下來，從 Key=3//第 5 個索引開始。
©”TNGD”.com
Key=3//第 5 個索引
9 > 3 → [2, 4, 5, 6 , 3, 9]
6 > 3 → [2, 4, 5, 3, 6, 9]
5 > 3 → [2, 4, 3, 5, 6, 9]
4 > 3 → [2, 3, 4, 5, 6, 9]
1 > 3==！停止
結果:[2, 3, 4, 5, 6, 9]
避免交換鍵索引在每次迭代中，下面是一個優化的插入排序算法，其中key 元素將在最後一步切換。
InsertionSort(arr[])
對於 j=1 到 arr.length
key=arr[j]
i=j – 1
當 i > 0 和 arr[i] > 鍵
arr[i+1]=arr[i]
i=i – 1
arr[i+1]=鍵
JavaScript 中的插入排序實現:
這裡，插入排序是用Javascript實現的。
©”TNGD”.com
插入排序的性質
空間複雜度 – O(1)時間複雜度 – O(n), O(n* n), O(n* n) 分別針對最佳、平均和最壞情況。最佳情況——數組已經排序平均情況——數組隨機排序最壞情況——數組反向排序。就地排序:是穩定的:是
插入排序的應用算法
插入排序在以下情況下使用:
數組中的元素較少
#4。基數排序算法
基數排序是一種排序算法，其工作原理是首先對具有相同位值的元素進行分組，然後按升序或降序對它們進行排序。基數排序算法的出現是為了擴展計數排序以實現更好的時間複雜度。
基數排序的工作原理
對於每個數字，n，其中 n 從最小有效數字到最高有效數字一個數字，使用 Count Sort 根據第 n 位對輸入數組進行排序。我們使用計數排序，因為它是一種穩定的算法。
示例:
給定輸入數組 [10, 21, 17, 34, 44, 11, 654, 123]，我們會根據算法按照最低位/個位排序
0: 10
1: 21, 11
2:
3:123
4:34、44、654
5:
6:
7: 17
8:
9:
因此，數組變為 [10, 21, 11, 123, 34, 44, 654].
讓我們根據十位數排序:
0:
1: 10, 11, 17
2: 21, 123
3:34
4:44
5:654
6:
7:
8:
9:
現在，數組是:[10, 11, 17, 21, 123, 34, 44, 654]
最後我們按照最高位（百位）排序:
0: 010 011 017 021 034 044
1: 123
2:
3:
4:
5:
6: 654
7:
8:
9:
結果:[10, 11, 17, 21, 34, 44, 123, 654]，這樣就排序了。這就是算法的工作原理。
基數排序在 C 中的實現:
C 中實現的基數排序
©”TNGD”.com
#5.歸併排序算法
歸併排序是一種結合了分而治之算法原理的排序算法。它將數組拆分為子問題，即劃分，當子問題的解決方案準備就緒時，它將所有子問題的結果組合起來解決主要問題。
歸併排序是如何工作的?
這個過程只涉及三個步驟:
劃分——將數組拆分成子問題征服– 使用相同的算法對子問題進行排序Combine – 合併結果
示例:
使用未排序的數組[6, 5, 12, 10, 9, 1]
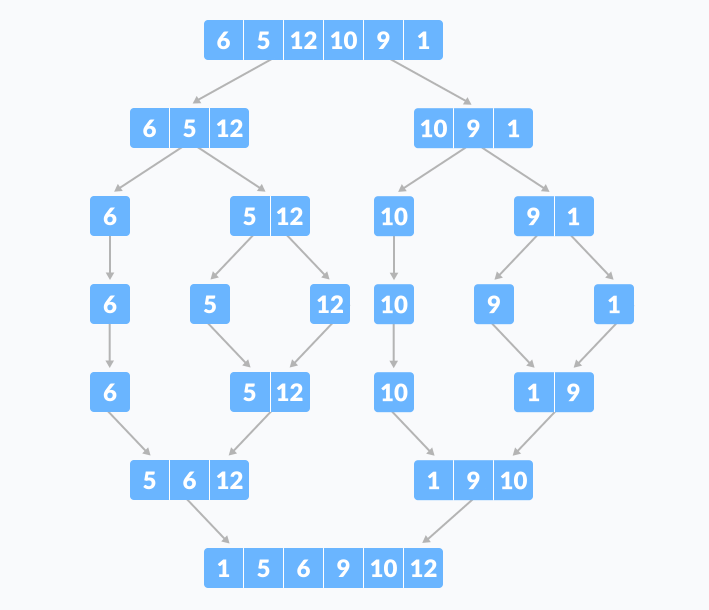歸併排序只需要三步。
©”TNGD”.com
合併排序在 JavaScript 中的實現
Javascript 中顯示的合併排序算法。
©”TNGD”.com
屬性
空間複雜度 – O(n)時間複雜度 – O(n*log(n))。 log(n) 因素是因為遞歸關係。In-Place Sorting – 典型實現中沒有 Stable – 是Parallelizable – 是
Applications
E-commerceExternal sortingInversion count problem
#6.快速排序算法
快速排序是一種基於分而治之算法的排序算法。
快速排序算法的工作原理
它涉及以下步驟:
選擇一個元素作為樞軸，在我們的例子中，樞軸是最後一個元素。分區-對通過確保所有小於主元的值都在左側，而所有大於主元的值都在右側。在確保主元向左和向右正確細分的同時，遞歸調用快速排序。
Python3 中的快速排序實現
Python3 中的快速排序算法。
©”TNGD”.com
快速排序應用
此算法用於:
空間複雜度很重要時間複雜度很重要編程語言適用於遞歸。
#7。計數排序算法
計數排序是一種通過計算數組中每個值的出現次數來對輸入數組元素進行排序的算法。排序是通過將出現映射為輔助數組索引然後存儲在輔助數組中來完成的。
計數排序的工作原理
示例:
給定輸入=[2, 5, 3, 1, 4, 2]
創建每個唯一值出現的列表
Count=[0, 0 , 0, 0, 0, 0]
Val: 0 1 2 3 4 5
遍歷輸入列表並將索引迭代一個（對於每個值）
例如，列表中的第一個值是2，則將計數列表的第二個索引值加一，值為2:
Count=[0, 0, 1, 0 , 0, 0]
Val: 0 1 2 3 4 5
繼續實現列表中每個值的總計數:
Count=[ 0, 1, 2, 1, 1, 1]
Val: 0 1 2 3 4 5
您可以輕鬆創建排序輸出，因為您知道每個輸出的出現列表中的值。循環遍歷出現列表並將相應的值添加到輸出數組。
例如，輸入列表中沒有 0，但出現了值 1，現在將輸出數組添加一次:
Output=[ 1 ]
對於值 2，我們有兩次出現，所以添加到輸出列表:
Output=[ 1, 2, 2 ]
繼續，直到你有一個排序的輸出列表:
Output=[ 1, 2, 2, 3, 4, 5 ]
Counting Sort Implementation in JavaScript
計數按照 Javascript 中的實現排序。
©”TNGD”.com
屬性
空間複雜度 – 0 (k)最佳情況性能 – 0(n+k)平均情況性能 – 0(n+k)最壞情況性能 – 0(n+k)穩定 – 是
#8。堆排序算法
堆排序是一種優秀的排序算法，它通過使用最大/最小堆來工作。堆是一種獨特的基於樹的數據結構，它遵循堆屬性。這意味著，對於最大堆，樹中的子節點小於或等於父節點。
該算法是一種不穩定的算法，因此在排序時不會保留初始順序。它具有 O(n log n) 的最佳和最壞情況時間複雜度，並且由於它是一種基於比較的算法，因此可用於非數值數據集。
Heapsort 的優點
最小內存使用量易於理解和實現高效
缺點
昂貴不穩定
Java 中的堆排序實現
©”TNGD”.com
©”TNGD”.com
Java實現的堆排序算法。
©”TNGD”.com
#9。桶排序算法
桶排序是一種排序算法，它將輸入數組元素細分為更小的組，稱為桶。然後使用您選擇的算法對存儲桶進行排序。排序後，將桶合併以形成最終的排序數組。
使用桶排序，同樣的數組可以在0(n)次時間內完成。
桶排序偽代碼
桶排序將輸入數組元素細分為更小的組，稱為桶。
©”TNGD.com
#10。 Shell 排序算法
Shell 排序通常是插入排序的變體。它根據使用的順序，通過減少元素之間的間隔來對元素進行排序。
Shell 排序的工作原理
有一個數組 n，我們不斷減少 n 的值，直到它變為 1。如果每第 n 個元素的子列表都已排序，則稱數組是 n 排序的。
算法
步驟 1 – StartStep 2 – 初始化間隙大小值，例如，n.第 3 步 – 將列表細分為更小的列表。我們需要與 n 相等的間隔。第 4 步 – 使用插入排序對子列表進行排序。第 5 步 – 重複第 2 步，直到列表被排序。第 6 步 – 打印排序後的列表。第 7 步 – 停止
How Shell Sort已實施
有一個數組 n，我們不斷減少 n 的值，直到它變為 1。
©”TNGD”.com
結論
排序算法是計算機科學的一個基本概念，因為它們有效地組織和管理大數據量。每種算法在簡單性、效率和空間複雜性方面都有其優缺點。最適合您的算法取決於您要解決的具體問題，以及數據的大小和復雜性。