© pinkeyes/Shutterstock.com
Dijkstra 算法只是我們所說的最短路徑算法的一個例子。簡而言之，這些算法用於查找圖的頂點之間的最短距離（或路徑）。
雖然最短路徑可以用多種方式定義，例如時間、成本或距離，但它通常是指節點之間的距離。如果您想了解更多關於 Dijkstra 算法的工作原理以及它的用途，那麼您來對地方了。
什麼是Dijkstra算法?
簡單來說，Dijkstra算法是一種尋找圖中節點之間的最短路徑。指定一個源節點，然後使用該算法計算該節點與所有其他節點之間的距離。
與其他一些最短路徑算法相反，Dijkstra 只能處理非負加權圖。也就是說，每個節點的值代表一些數量的圖形，例如成本或距離，並且所有值都是正數。
算法
在我們深入研究如何使用 Dijkstra 算法實現之前代碼，讓我們運行一下涉及的步驟:
首先，我們初始化一個空的優先級隊列；讓我們稱之為“Q”。這是使用該算法最有效的方法，因為它確保我們總是選擇下一個最接近源節點的頂點。由於我們還不知道每個頂點到源節點的距離，我們初始化所有頂點距離到無窮大。源頂點或源節點的距離也設置為 0，因為這是我們的起點。然後將源節點添加到優先級為 0 的優先級隊列中。首先，具有最小的頂點distance 從隊列中刪除。這個頂點被稱為“u”，相鄰的頂點被指定為“v”。計算源節點通過u到每個v的距離，如果距離小於當前到v的距離，則更新距離。一旦計算出v，將其插入優先級隊列，其優先級設置為等於它到源頂點的距離。這確保了具有較小距離的頂點被優先考慮，通過首先考慮最近的未訪問頂點來保持算法的效率。
Dijkstra 算法的功能
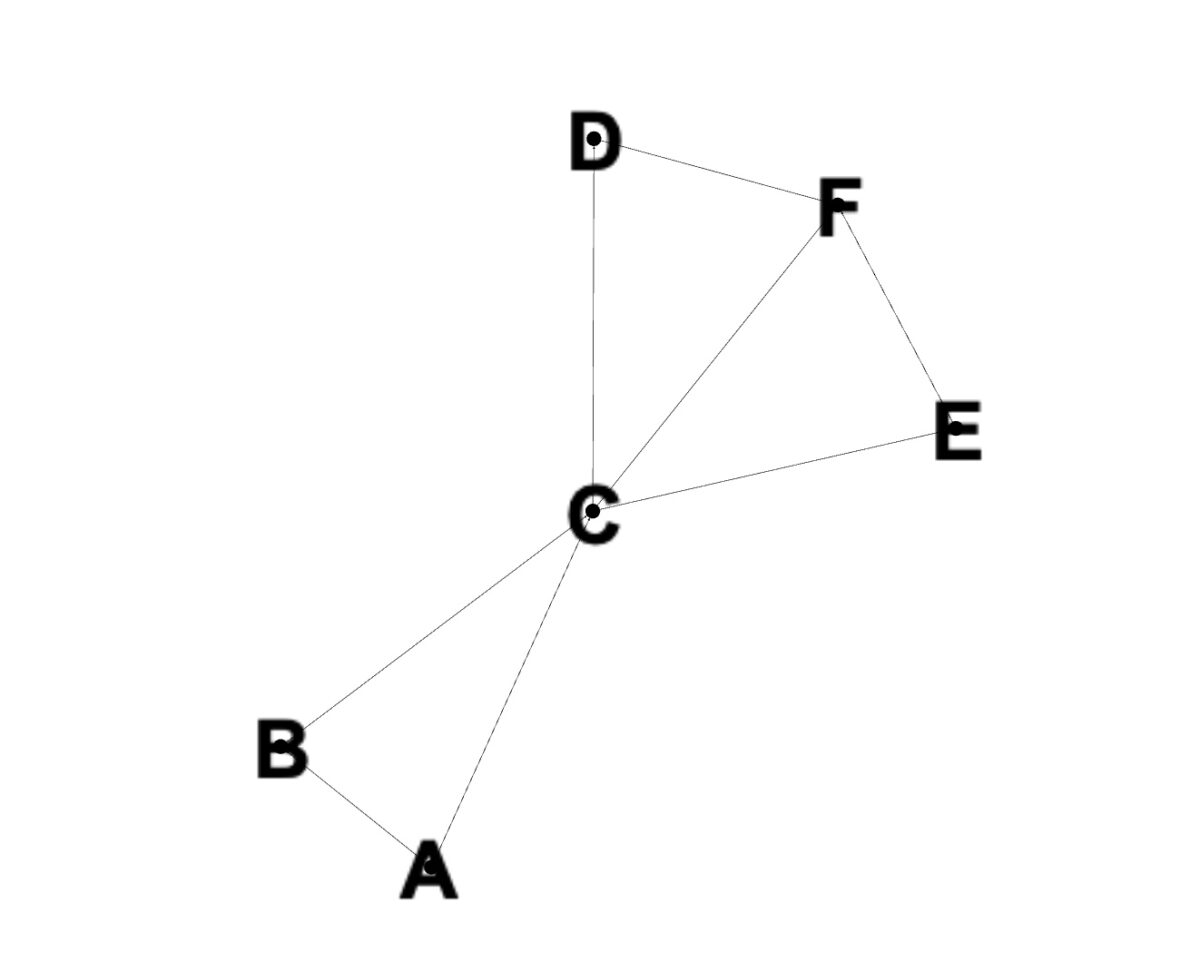頂點 A 到 F.
©”TNGD”.com
現在我們已經介紹了 Dijkstra 算法背後的基礎知識，讓我們通過示例看一下它是如何工作的。首先，拿一個節點排列如下的圖:
我們有頂點 A 到 F，它們通過各種路徑相互連接。這些連接也稱為邊。如果我們選擇 A 作為我們的起始頂點，則其他節點的所有路徑值都設置為無窮大，如前所述。
然後我們轉到每個頂點並更新其路徑長度。如果到相鄰節點的計算距離小於當前到該頂點的距離，則更新該距離。
如果我們將每個頂點的優先級設置為等於它到源的距離，我們就可以避免訪問節點兩次。當訪問一個未訪問的節點時，我們首先尋找最短路徑長度。重複此過程，直到訪問了每個節點併計算了與源節點的距離。
使用堆實現 Dijkstra 算法
是時候為 Dijkstra 算法實現一些代碼了進入 Python，看看它是如何工作的。我們將從使用稱為堆的優先級隊列的簡單實現開始。代碼可以表示如下:
import heapq import sys def dijkstra_heap(adj_matrix, source): num_vertices=len(adj_matrix) distances=[sys.maxsize] * num_vertices distances[source]=0 visited=[False] * num_vertices heap=[(0, source)] while heap: current_distance, current_vertex=heapq.heappop(heap) visited[current_vertex]=True for neighbor_vertex in range(num_vertices): weight=adj_matrix[current_vertex][neighbor_vertex] 如果沒有訪問[neighbor_vertex] and weight !=0: distance=current_distance + weight if distances[neighbor_vertex]: distances[neighbor_vertex]=distance heapq.heappush(heap, (distance, neighbor_vertex)) 返回距離 adj_matrix=[ [0, 2, 2 , 0, 0, 0], [2, 0, 2, 0, 0, 0], [2, 2, 0, 2, 2, 6], [0, 0, 2, 0, 2, 2], [0, 0, 2, 2, 0, 2], [0, 0, 6, 2, 2, 0] ] 距離=dijkstra_heap(adj_matrix, 0) print(di stances)
代碼解釋
讓我們一步一步分解這段代碼，這樣我們就可以理解發生了什麼。
導入模塊
首先，我們導入“heapq”和“sys”模塊。第一個模塊允許我們使用堆數據結構，而第二個模塊允許我們使用最大整數值。這是必需的，因為我們將頂點距離初始化為無窮大。
定義 Dijkstra 算法
接下來，我們將“dijkstra_heap”定義為具有兩個參數的函數——“adj_matrix”和“來源”。這些圖分別表示為鄰接矩陣和源節點的索引。
訪問節點
在這個塊中，我們計算頂點的數量.然後，我們將源頂點到每個目標頂點的距離初始化為無窮大，如前所述。源節點的距離也設置為零。
然後創建一個名為“visited”的列表，它被初始化為“False”。這意味著在我們計算出它們與源之間的距離之前，節點最初被認為是未訪問過的。還創建了一個稱為“堆”的優先級隊列，其中起始頂點和與源節點的距離指定為元組。
更新最短路徑長度
接下來，我們有一個“while”循環，一直運行到隊列為空。第一行從堆中獲取與源頂點距離最短的頂點，第二行在計算出該距離後將頂點標記為已訪問。
我們在其後使用“for”循環，它遍歷我們當前關注的頂點的所有鄰居。檢索每條邊的權重，並檢查是否已訪問鄰居節點以及權重是否非零。然後使用從源到當前節點的距離計算到鄰居節點的距離。
我們有另一個“if”語句，它檢查計算的距離是否短於我們的當前最短距離“距離”列表。如果是這樣，下一行更新這個值。最後，將相鄰頂點及其與源節點的距離添加到堆中。
結果輸出
此過程完成後，從源節點到圖中的所有其他節點都返回到控制台。
倒數第二個代碼塊簡單地將我們正在查看的圖表示為鄰接矩陣，其中單元格 {i, j} 中的值表示連接兩個頂點的邊的權重。
最後的代碼只是告訴系統計算最短路徑距離，然後將這些打印到控制台。
代碼的實現
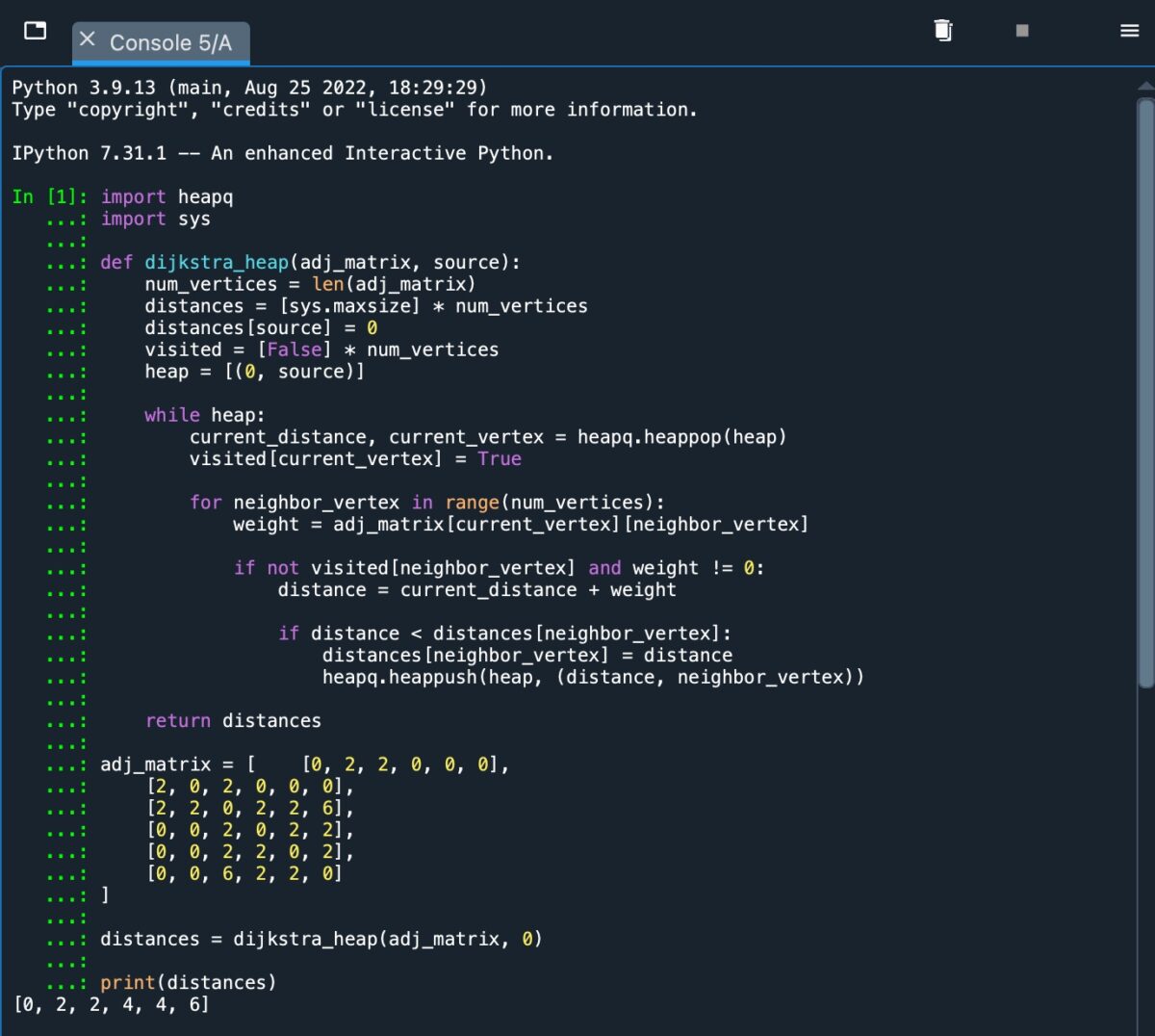一個簡單的實現heap.
©”TNGD”.com
從截圖中我們可以看到，我們收到一個輸出[0, 2, 2, 4, 4, 6]，代表最短路徑距離從源節點 A 到節點 B、C、D、E 和 F。
最佳和最差使用Dijkstra 算法的案例
一般來說，Dijkstra 算法被認為是高效的，儘管某些算法在特殊情況下可能表現更好。話雖如此，讓我們看看 Dijkstra 算法在最佳、平均和最壞情況下的時間和空間複雜度。
Dijkstra 算法的時間複雜度
通常，對於每種情況，我們只有一種複雜性。但是，使用 Dijkstra 的算法，情況就不那麼明確了。這是因為您可以用不同的方式實現該算法，主要是通過使用優先級隊列。
使用優先級隊列時，可以使用二叉堆方法或斐波那契堆方法。通常，斐波那契堆會導致更高效的性能，以及更好的 O((E + V) log V) 的最壞情況時間複雜度，其中 E 是邊數，V 是頂點數。
如果您沒有使用優先級隊列並且圖形很密集，那麼最壞情況下的複雜度可能會像 O(V2 log V) 一樣低效。
關於平均情況，時間複雜度更有利。平均情況是指使用優先級隊列計算到每個頂點的最小距離。
最好的情況，嚴格來說，是一種不尋常的情況。您可能不會費心使用該算法來解決它。這是因為最好的情況是源頂點與目標頂點相同。這意味著迭代僅在一個循環後就終止了。
事實上，複雜度與一般情況相同。但是由於 E 和 V 的值都等於 1，所以這被簡化為 O(1)。如果您使用堆來實現您的算法，那麼最佳情況下的複雜度將變為 O(E* log V)。這是因為隊列中的頂點最多為 O(E)。
Dijkstra 算法的空間複雜度
和時間複雜度一樣，算法的空間複雜度取決於你的實現。如果您使用鄰接表來表示您的圖形和 Fibonacci 堆或常規堆，則復雜度等於 O(V+E)。這是因為頂點到源的距離，以及頂點之間的邊，需要存儲在內存中。
但是，如果使用鄰接矩陣，複雜度會降低到 O( V2).這是因為您需要存儲頂點距離以及 V * V 矩陣來表示邊。
總結
總而言之，Dijkstra 算法是使用的眾多算法之一用於計算圖中的最短路徑長度，非常有用。雖然有很多方法可以實現該算法，但使用某種描述的優先級隊列通常是最好的選擇。
在這些方法中，使用斐波那契堆往往是最有效的，特別是對於大型圖。然而，對於較小的圖，一個更簡單的優先級隊列可能就足夠了。
Up Next
Dijkstra 的最短路徑算法解釋及示例常見問題解答（常見問題解答）
什麼是 Dijkstra 算法?
該算法用於計算圖上節點之間的最短路徑長度。這是一種迭代方法，從與源節點的最短距離開始，然後更新到相鄰節點的距離。
Dijkstra 算法的局限性是什麼?
該算法無法處理負權邊，會導致結果不正確。
Dijkstra 算法的時間複雜度是多少?
時間複雜度取決於您是否使用優先級隊列，以及您如何實現它。在最好的情況下，只需要一次迭代，複雜度是 O(1)。
否則，最好的情況是 O(E* log V) 或 O(E + V log V) ，這取決於您使用的是標準堆還是 Fibonacci 堆。
在任何一種情況下，平均情況和最壞情況的複雜性都是相同的。如果您根本不使用優先級隊列，最壞的情況可能相當於 O(V2 log V)。
Dijkstra 算法的空間複雜度是多少?
這取決於實現，但可以是從 O(V2) 到 O(V + E) 的任何地方。
你能在有環的圖上使用 Dijkstra 算法嗎?
可以，只要權重邊都不為負。
Dijkstra 算法有哪些不同的實現方式?
您可以使用優先級隊列，例如堆或 Fibonacci 堆。通常，斐波那契堆會導致更高效的結果和更大的圖。
Dijkstra 算法的替代方案是什麼?
其他最短路徑算法包括 A * 算法、Bellman-Ford 算法和 Floyd-Warshall 算法。 A* 往往更快，但需要更多內存。
與 Dijkstra 不同，Bellman-Ford 和 Floyd-Warshall 都可以處理負權重邊，但兩者都比 Dijkstra 效率低 – 它們的時間複雜度為 O(VE ) 和 O(V3) 分別。