圖的廣度優先搜索 (BFS) – 解釋和示例

計算機科學家經常使用圖形來表示數據。圖可以表示各種關係，從地圖和化合物到社會關係和計算機網絡。我們可以對圖使用許多算法，例如 Dijkstra 算法、深度優先搜索 (DFS) 算法和廣度優先搜索（或 BFS）算法。雖然您可以使用這兩種算法來遍歷圖的節點，但 BFS 更適合未加權的圖。在本文中，我們將探討 BFS 的工作原理及其應用。

什麼是 BFS?

BFS 是一種搜索算法。該算法從源節點開始遍歷，然後訪問相鄰節點。在此之後，算法選擇下一個深度級別的最近節點，然後訪問下一個未探索的節點，依此類推。由於 BFS 算法在進入下一層之前會訪問每一層的節點，這就是“廣度優先”這個名稱的由來。我們通過跟踪已訪問和未訪問的節點來確保我們只訪問每個節點一次。您可以使用 BFS 來計算路徑距離，就像使用 Dijkstra 算法一樣。

BFS背後的算法

我們可以用以下偽代碼表示基本算法:

BFS(graph, start): queue=[start] visited=set(start) while queue is not empty: node=dequeue(queue) process(node) for neighbor in graph.neighbors(node): 如果鄰居不在 visited: visited.add(neighbor) enqueue(queue, neighbor)

在這種情況下，我們將圖定義為“graph”，“start”是起始節點。

我們實現了一個隊列結構來保存未訪問的節點，以及一個“visited”集合來保存被訪問的節點。

“while”循環一直持續到隊列為空，並開始逐級處理節點。 “dequeue”函數在第一個節點被訪問時將其從隊列中移除。

“process”函數在節點上執行一些所需的功能，例如更新到其鄰居的距離或將數據打印到

“for”循環遍歷當前節點的所有鄰居，檢查該節點是否已經被訪問過。如果不是，則使用“enqueue”函數將其添加到隊列中。本質上，每個級別的節點都存儲在隊列中，並添加它們的鄰居以在下一個深度級別訪問。這使我們能夠確定源節點與圖中每個其他節點之間的最短路徑。

BFS 的工作

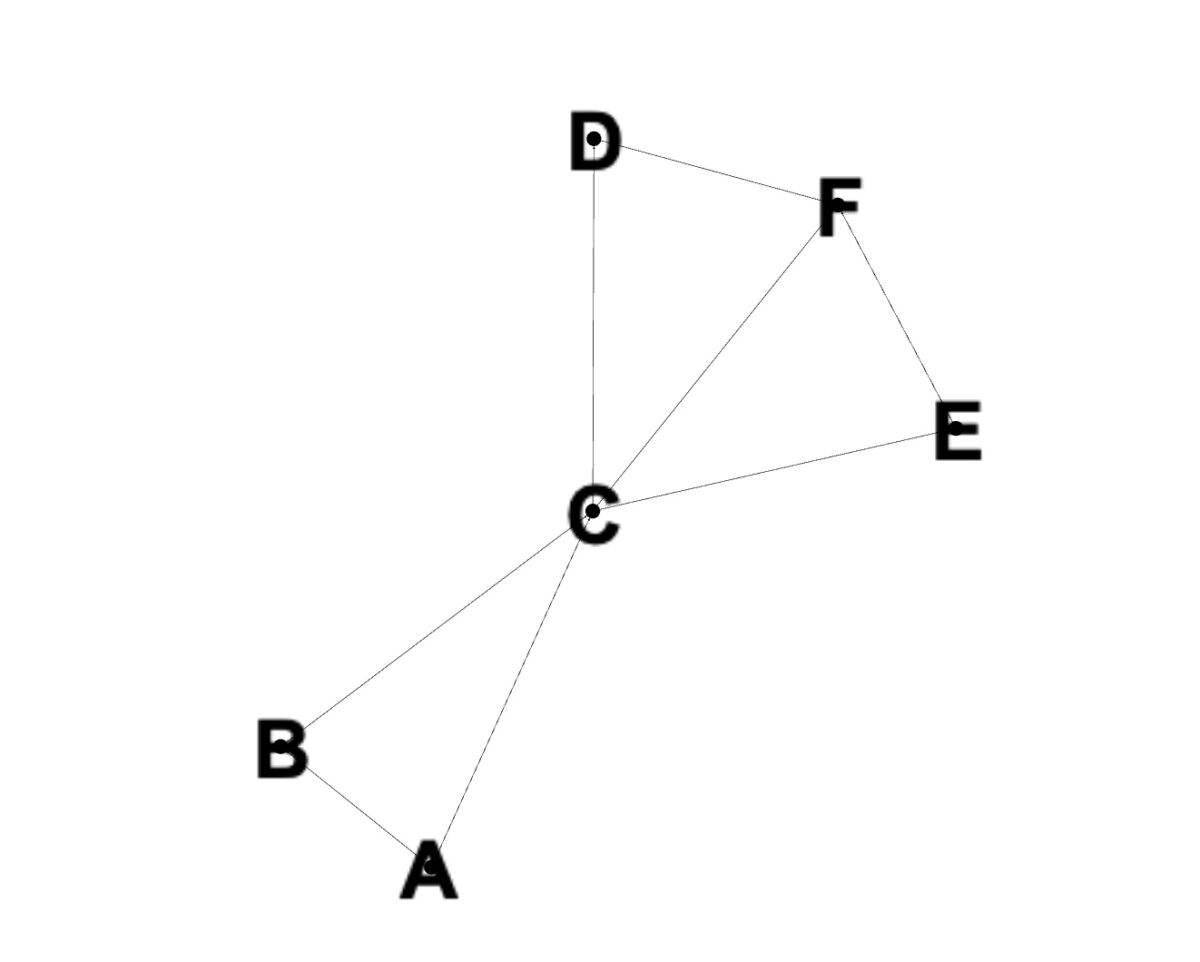我們將在以下代碼示例中使用此圖。

©”TNGD”.com

解釋完基礎知識，是時候看看 BFS 在實踐中是如何工作的了。我們將使用具有節點 A、B、C、D、E 和 F 的圖形來說明這一點，如圖所示。下面的代碼顯示瞭如何使用 Python 編程語言為此圖實現 BFS。

from collections import defaultdict, deque def bfs(graph, start): queue=deque([start]) visited=set([start] ) while queue: node=queue.popleft() print(node) for neighbor in graph[node]: 如果鄰居不在 visited: visited.add(neighbor) queue.append(neighbor) graph=defaultdict(list) edges=[ (“A”,”B”),”A”,”C”), (“B”,”C”), (“C”,”D”), (“C”,”E”), (“C”,”F”), (“D”,”F”), (“E”,”F”) for edge in edges: graph[edge[0]].append(edge[0]) graph[ edge[1]].append(edge[0]) bfs(graph,”A”)

代碼解釋

首先，我們導入“defaultdict”和“deque”類來自“收藏”模塊。這些用於創建具有默認鍵值的字典，並創建允許添加和刪除元素的隊列。

接下來，我們使用兩個參數定義“bfs”函數，“graph”和“開始”。我們將“圖”參數作為一個字典，其中頂點作為鍵，相鄰頂點作為值。這裡，“start”指的是算法開始的源節點。

“queue=deque([start])”創建一個以源節點為唯一元素的隊列，“visited=set ([start])”創建一組以源節點為唯一元素的已訪問節點。

“while”循環一直持續到隊列為空。 “node=queue.popleft()”從隊列中移除最左邊的元素並將其存儲在“node”變量中。 “print(node)”打印這些節點值。

“for”循環遍歷每個鄰居節點。 “if neighbor not visited”檢查鄰居是否被訪問過。 “visited.add(neighbor)”將鄰居添加到已訪問列表，“queue.append(neighbor)”將鄰居添加到隊列的右端。

在此之後，我們創建一個默認值名為“圖”的字典，並定義圖的邊。 “for”循環遍歷每條邊。 “graph[edge[0]].append(edge[1])”將邊的第二個元素添加為第一個元素的鄰居，並將邊的第一個元素添加為第二個元素的鄰居。這樣就構建了圖。

最後，我們在“圖”上調用“bfs”函數，源節點為“A”。

代碼實現

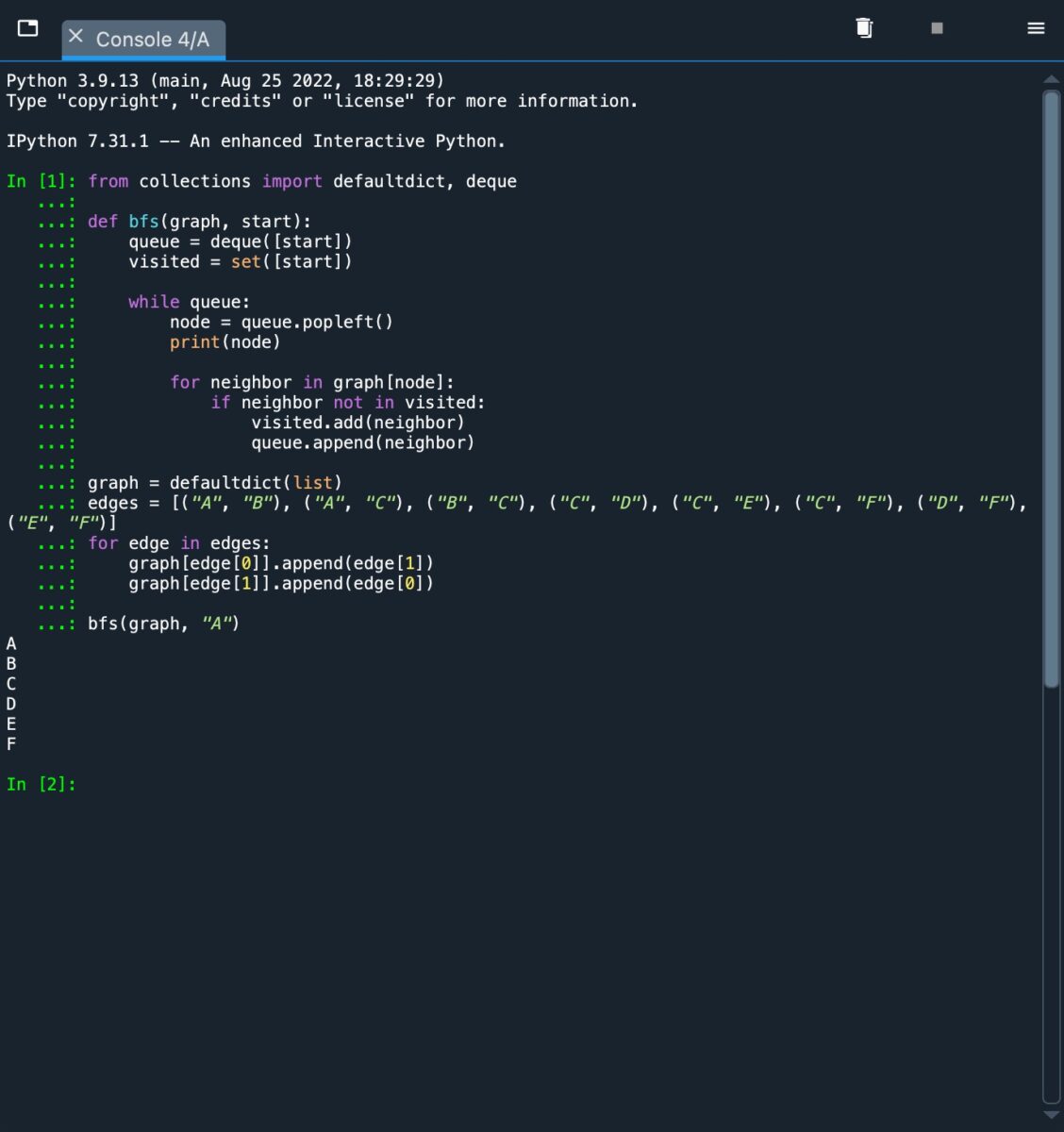這是 BFS 算法的樣子通過連接圖實現和運行。

©”TNGD”.com

在屏幕截圖中，我們可以看到輸出 [A, B, C, D, E F]。這是我們所期望的，因為 BFS 在移動到下一個深度之前探索每個深度級別的節點。回顧圖表，我們看到 B 和 C 將被添加到隊列中並首先被訪問。訪問了 B，然後將 A 和 C 添加到隊列中。由於已經訪問過 A，接下來訪問 C，然後刪除 A。在此之後，C 的鄰居 D、E 和 F 被添加到隊列中。然後訪問這些，並打印輸出。

對不連通圖使用 BFS

我們之前對連通圖使用 BFS。但是，當節點未全部連接時，我們也可以使用 BFS。我們將使用相同的圖表數據，因為修改後的算法可以用任何一種圖表來說明。修改後的代碼為:

from collections import defaultdict, deque def bfs(graph, start): queue=deque([start]) visited=set([start]) while queue: node=queue.popleft() print (node) for neighbor in graph[node]: if neighbor not in visited: visited.add(neighbor) queue.append(neighbor) for node in graph.keys(): if node not in visited: queue=deque([節點]) visited.add(node) while queue: node=queue.popleft() print(node) for neighbor in graph[node]: if neighbor not in visited: visited.add(neighbor) queue.append(neighbor) 圖=defaultdict(list) edges=[(“A”,”B”), (“A”,”C”), (“B”,”C”), (“C”,”D”), (“C”,”E”), (“C”,”F”), (“D”,”F”), (“E”,”F”)] 對於邊中的邊:graph[edge[0]]。追加（邊[1]）圖[邊[1]].追加（邊[0]） bfs(graph,”A”)

我們使用了一個額外的“for”循環。循環使用“graph.keys()”方法遍歷所有節點。如果 BFS 找到一個未訪問的節點並遞歸工作，它會啟動一個新隊列。通過這樣做，我們訪問了所有斷開連接的節點。請參見下圖的插圖。

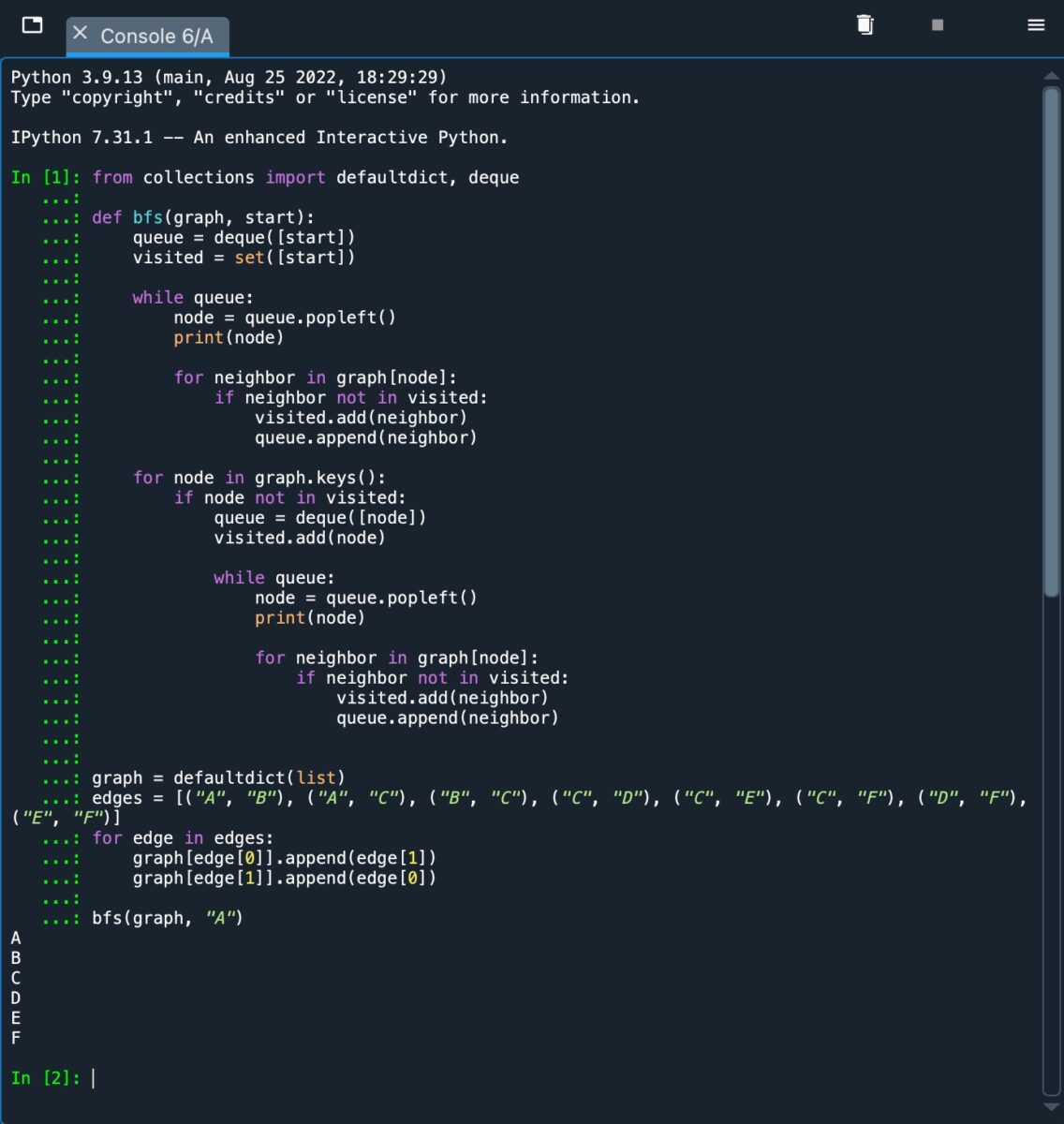這是 BFS 算法在一個斷開的圖上實現和運行的例子。

©”TNGD”.com

BFS 的最佳和最差用例

現在我們了解了 BFS 的工作原理，我們應該查看算法的時間和空間複雜度，以了解其最佳和最差用例。

BFS 的時間複雜度

CaseComplexityBestO(V + E)AverageO(V + E)WorstO(V + E)

我們可以看到時間複雜度在所有情況下都是一樣的，等於O(V + E)，其中 V 是頂點數，E 是邊數。在最好的情況下，我們只有一個節點，複雜度將為 O(1)，因為 V=1 且 E=0。在平均和最壞的情況下，算法會訪問它可以從源節點到達的所有節點，因此復雜度取決於兩種情況下圖的結構和大小。

BFS 的空間複雜度

CaseComplexityBestO(V)AverageO(V)WorstO(V)

同樣，我們看到所有情況下的複雜度都相同。無論圖形結構如何，該算法都會訪問每個節點。因此，複雜度取決於圖中頂點的數量。

總結

BFS 是遍歷圖中節點、計算路徑距離並探索節點之間關係的一種方法節點。它是探索網絡系統和檢測圖循環的非常有用的算法。 BFS 對於連通圖和非連通圖都相對容易實現。一個好處是所有情況下的時間和空間複雜度都相同。