Na verdade, existem duas maneiras de implementar o merge sort – a abordagem de cima para baixo e a abordagem de baixo para cima. É um bom momento para dar uma breve visão geral desses processos.
A abordagem de cima para baixo
Como o nome sugere, esse algoritmo começa no topo com a matriz inicial, divide o array ao meio, classifica recursivamente esses subarrays (ou seja, dividindo-os e repetindo o processo) e, em seguida, mescla os resultados em um array classificado.
A abordagem de baixo para cima
Por outro lado, a abordagem bottom-up depende de um método iterativo. Ele começa com uma matriz de um único elemento e, em seguida, mescla os elementos de cada lado enquanto os classifica. Essas matrizes combinadas e classificadas são mescladas e classificadas até que apenas um elemento permaneça na matriz classificada. A principal diferença é que, enquanto a abordagem de cima para baixo classifica cada subarray recursivamente, a abordagem de baixo para cima divide o array em arrays singulares. Em seguida, cada array é classificado e mesclado iterativamente.
Trabalho de classificação por mesclagem
Seguindo isso, um exemplo de trabalho de como a classificação por mesclagem é usada seria útil.
Digamos que nós tem uma matriz, arr. Arr=[37, 25, 42, 2, 7, 89, 14].
Primeiramente, realizamos uma verificação para ver se o índice esquerdo da matriz é menor que o índice direito. Se isso for verdade, o ponto médio é calculado. Isso é igual a “(start_index” + (“end_index”-1))/2, que, neste caso, é 3. Portanto, o elemento no índice 3 é o ponto médio, que é 2.
Dessa forma, este array de 7 elementos foi dividido em dois arrays de tamanho 4 e 3 para os subarrays esquerdo e direito respectivamente:
Array esquerdo=[37, 25, 42, 2]
Array à direita=[7, 89, 14]
Continuamos calculando o ponto médio novamente e dividindo os arrays em dois até que a divisão não seja mais possível. O resultado final é:
[37], [25], [42], [2], [7], [89], [14]
E então, nós pode começar a mesclar e classificar esses subarrays como tal:
[25, 37], [2, 42], [7,89], [14]
Esses subarrays são então mesclados e classificados novamente para fornecer:
[2, 25, 37, 45] e [7, 14, 89]
Finalmente, esses subarrays são mesclados e classificados para fornecer a classificação final array:
[2, 7, 14, 25, 37, 45, 89]
Implementação do Merge Sort
Até agora, nós cobrimos como o algoritmo de classificação por mesclagem funciona, as etapas envolvidas e o trabalho por trás dele com um exemplo. Então, finalmente chegou a hora de ver como implementar esse algoritmo usando código. Para fins ilustrativos, usaremos a linguagem de programação Python. O processo pode ser descrito usando o seguinte código:
def mergeSort(arr): if len(arr) > 1: mid=len(arr)//2 L=arr[:mid] R=arr[mid: ] mergeSort(L) mergeSort(R) i=j=k=0 while i len(L) e j len(R): se L[i]=R[j]: arr[k]=L[i] i +=1 else: arr[k]=R[i] j +=1 k +=1 while i len(L): arr[k]=L[i] i +=1 k +=1 while j len( R): arr[k]=R[j] j +=1 k +=1 def printList(arr): for i in range(len(arr)): print(arr[i], end=””) print () if__name__==’__main__’: arr=12, 11, 13, 5, 6, 7] print(“Dado array é”, end=”\n”) printList(arr) mergeSort(arr) print(“Ordenado array is”, end=”\n”) printList(arr)
Isso parece muito código, mas é administrável se o dividirmos.
Explicação do código
Em primeiro lugar, estamos definindo a função mergeSort como uma função do array “arr”.
A primeira instrução “if” verifica se o comprimento do array é maior que 1. Nesse caso, podemos prosseguir com a divisão do array.
Em seguida, calculamos o ponto médio do array e o dividimos em dois subarrays, “L” e “R”.
A função mergeSort é chamada recursivamente em L e R, dividindo-os até que cada subarray contenha apenas um elemento.
Nesse ponto, três variáveis são inicializadas com zero=i, j e k. Os dois primeiros são os índices inicial e final do subarray que está sendo operado. “k” é uma variável que controla a posição atual na matriz.
A próxima parte, começando com a instrução “while”, é a seção principal do algoritmo. O algoritmo é iterado em L e R, comparando os elementos em i e j e copiando o elemento menor para a matriz. Juntamente com k, essas variáveis de índice são incrementadas, de acordo com o operador de incremento “=-”.
A próxima seção de instruções “while” determina que quaisquer elementos restantes nas duas matrizes sejam copiados para a matriz inicial.
Estamos quase terminando. Em seguida, definimos a função printlist como uma função do array “arr”.
Por último, usamos a linha “if_name_==’_main_’” para garantir que o código seja executado somente quando o script for executado diretamente, e não quando é importado.
O array original é impresso como “Dado array é”, e o array final classificado é impresso como “Sorted array é”. A linha final imprime esta matriz classificada, após a matriz inicial ter sido mesclada e classificada de acordo com o código anterior.
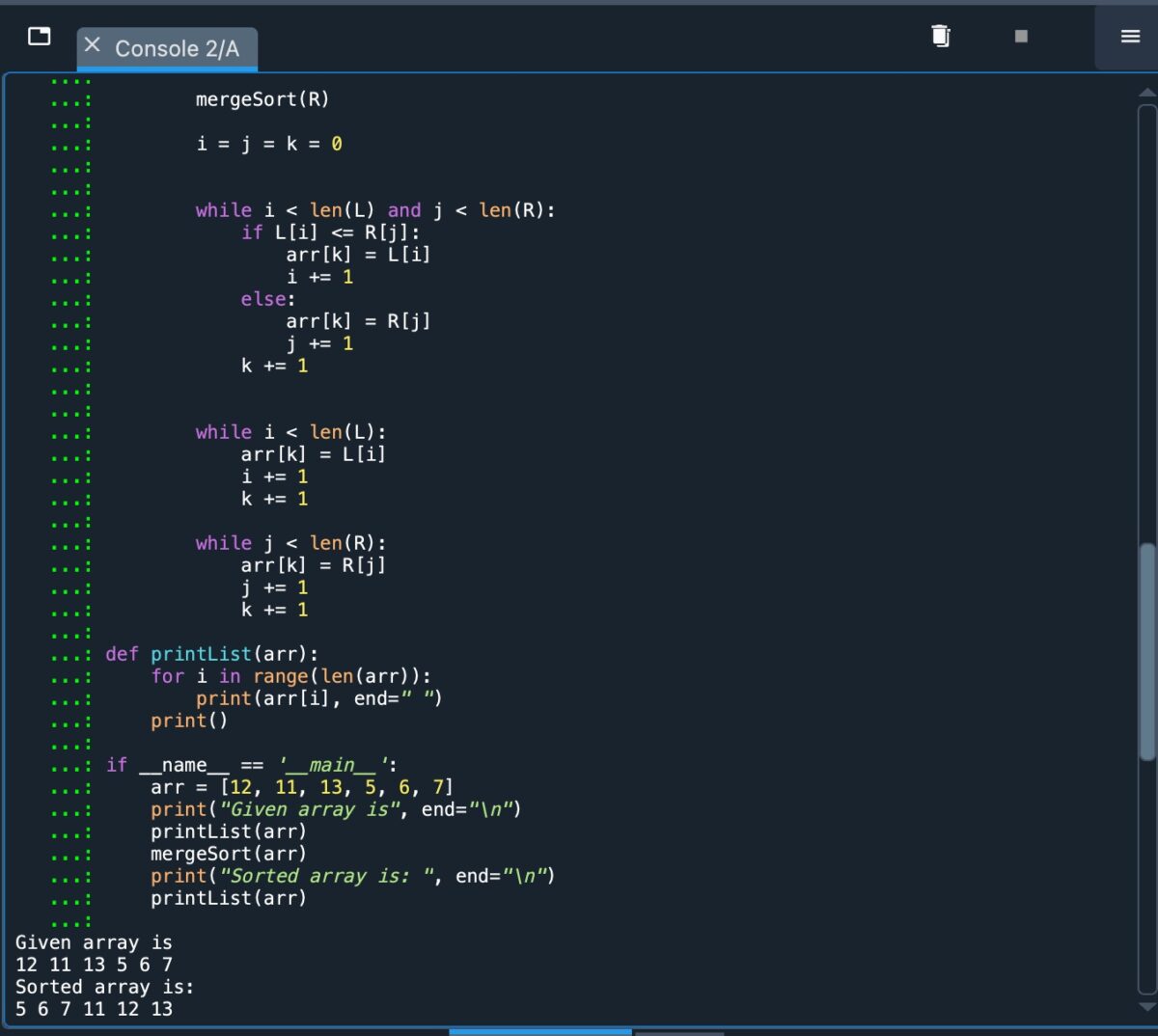
Para concluir, abaixo está uma captura de tela mostrando este código sendo implementado em Python:
Código Python para o algoritmo de classificação por mesclagem.
©”TNGD.com
Melhores e piores casos de uso de classificação por inserção
A classificação por mesclagem é um algoritmo simples, mas, como qualquer algoritmo , tem seus melhores e piores casos de uso. Estes são ilustrados abaixo em termos de complexidade de tempo e complexidade de espaço.
Complexidade de tempo com classificação por inserção
A complexidade de tempo em cada caso pode ser descrita na tabela a seguir:
O melhor caso refere-se a quando o array está parcialmente ordenado, o caso médio refere-se a quando o array está confuso e o pior caso refere-se a quando a matriz está em ordem crescente ou decrescente e você deseja o contrário. Como tal, isso exigiria mais classificação.
Felizmente, a classificação por mesclagem tem a mesma complexidade de tempo em cada caso, de O(n log n). Isso porque, em cada caso, cada elemento precisa ser copiado e comparado. Isso leva a uma dependência logarítmica no tamanho da entrada, pois o array é dividido recursivamente até que cada subarray contenha um elemento. No que diz respeito aos algoritmos de classificação, a complexidade de tempo da classificação por mesclagem é melhor do que alguns outros, como classificação por inserção e classificação por seleção. Como tal, o merge sort é um dos melhores algoritmos de classificação para trabalhar com grandes conjuntos de dados.
A seguir, examinaremos a complexidade espacial do merge sort.
Complexidade espacial do Merge Sort
Em comparação com outros algoritmos de classificação, a complexidade de espaço da classificação por mesclagem não se sai tão bem Isso porque, em vez de uma complexidade de O(1) (onde o uso da memória é constante e apenas uma variável temporária é armazenada), o merge sort tem uma complexidade de espaço de O(n), onde n é o tamanho da entrada. No pior caso, n/2 arrays temporários devem ser criados, cada um com tamanho n/2. Isso significa que há um requisito de espaço de O(n2/4) ou O(n2). Mas, na média e nos melhores casos, o número de arrays necessários é log(n) base 2, o que significa que a complexidade é proporcional a n. No geral, a complexidade do merge sort é relativamente boa e o algoritmo é adequado para grandes conjuntos de dados, mas o uso de memória é mais significativo do que outros métodos.
Resumo
Em conclusão, as vantagens e desvantagens do algoritmo de ordenação por mesclagem foram explicadas, juntamente com o funcionamento do algoritmo, ilustrado com exemplos. O Merge sort é um algoritmo de classificação adequado para grandes conjuntos de dados, mesmo que seu uso de memória seja relativamente alto. Resumindo, é um algoritmo relativamente simples de entender e excelente para implementar em muitos ambientes.