© pinkeyes/Shutterstock.com
O algoritmo de Dijkstra é apenas um exemplo do que chamamos de algoritmo de caminho mais curto. Em poucas palavras, são algoritmos usados para encontrar a menor distância (ou caminho) entre os vértices de um grafo.
Embora o caminho mais curto possa ser definido de várias maneiras, como tempo, custo ou distância, ele geralmente se refere à distância entre os nós. Se você quiser saber mais sobre como o algoritmo de Dijkstra funciona e para que você pode usá-lo, você está no lugar certo.

O que é o algoritmo de Dijkstra?
Em termos simples, o algoritmo de Dijkstra é um método para encontrar o caminho mais curto entre os nós de um grafo. Um nó de origem é designado e, em seguida, a distância entre esse nó e todos os outros nós é calculada usando o algoritmo.
Ao contrário de alguns outros algoritmos de caminho mais curto, o de Dijkstra só pode funcionar com gráficos ponderados não negativos. Ou seja, gráficos onde o valor de cada nó representa alguma quantidade, como custo ou distância, e todos os valores são positivos.
O algoritmo
Antes de mergulharmos em como implementar o algoritmo de Dijkstra usando código, vamos executar as etapas envolvidas:
Primeiro, inicializamos uma fila de prioridade vazia; vamos chamar isso de “Q”. Esta é a maneira mais eficiente de usar o algoritmo, pois garante que sempre selecionemos o próximo vértice mais próximo do nó de origem. Como ainda não sabemos as distâncias de cada vértice ao nó de origem, inicializamos todas as distâncias dos vértices ao infinito. A distância do vértice de origem, ou nó de origem, também é definida como 0, pois este é o nosso ponto de partida. O nó de origem é então adicionado à fila de prioridade com uma prioridade de 0. Para começar, o vértice com o menor distância é removida da fila. Esse vértice é chamado de “u” e os vértices vizinhos são designados como “v”. A distância do nó de origem para cada v até u é calculada e, se a distância for menor que a distância atual para v, a distância é atualizada. Uma vez que v é calculado, ele é inserido na fila de prioridade com sua prioridade definida para ser equivalente à sua distância do vértice de origem. Isso garante que os vértices com distâncias menores sejam priorizados primeiro, mantendo a eficiência do algoritmo considerando primeiro os vértices não visitados mais próximos.
Funcionamento do Algoritmo de Dijkstra
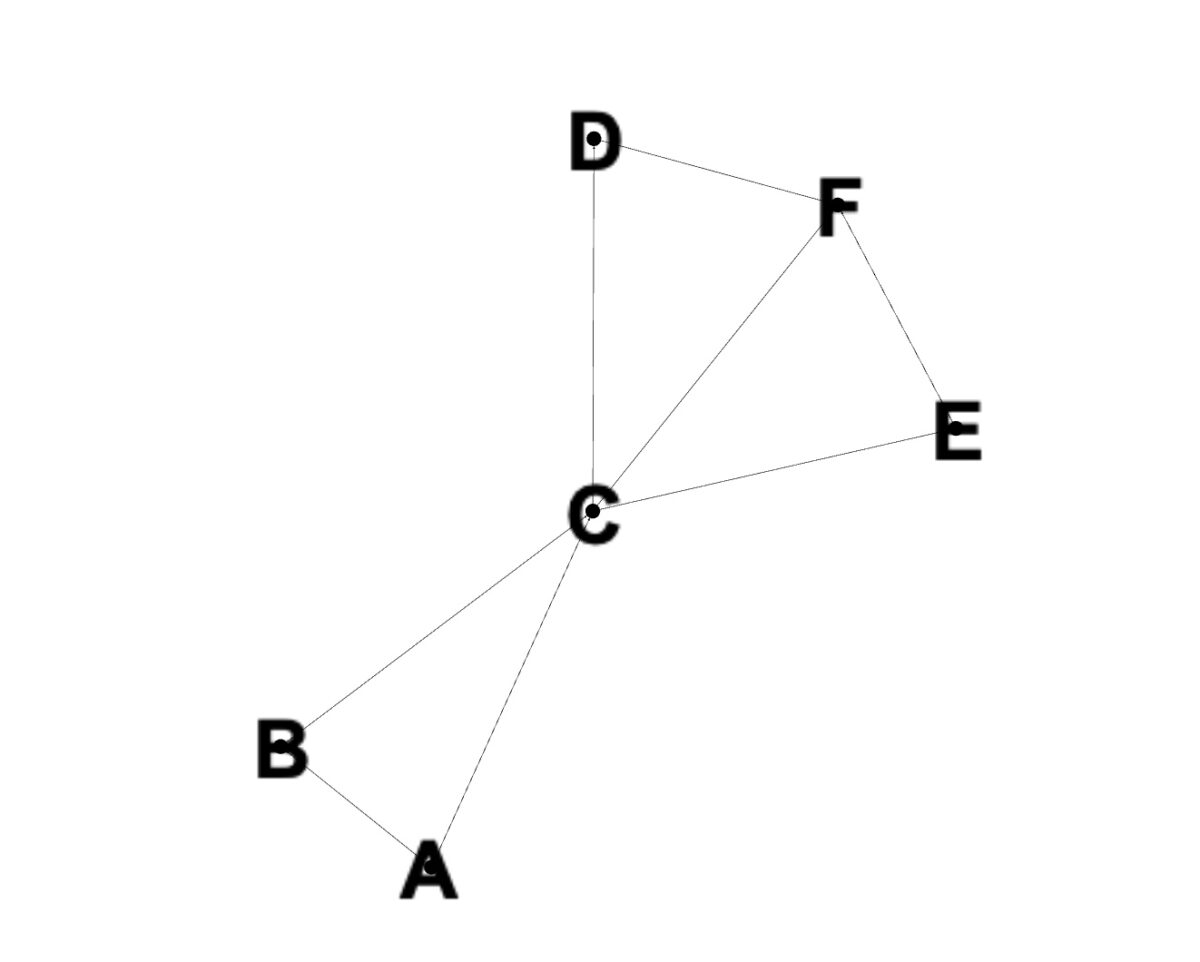 Vértices de A a F.
Vértices de A a F.
©”TNGD.com
Agora que abordamos o básico por trás do algoritmo de Dijkstra, vamos dar uma olhada em como ele funcionaria com um exemplo. Primeiro, pegue um grafo com nós organizados da seguinte forma:
Temos os vértices de A a F, que estão conectados entre si por vários caminhos. Essas conexões também são conhecidas como arestas. Se escolhermos A como nosso vértice inicial, todos os valores de caminho para os outros nós serão definidos como infinitos, conforme discutido anteriormente.
Em seguida, vamos a cada vértice e atualizamos seu comprimento de caminho. Se a distância calculada para o nó adjacente for menor que a distância atual para este vértice, a distância é atualizada.
Se definirmos a prioridade de cada vértice igual à sua distância da fonte, evitamos visitar os nós duas vezes. Ao visitar um nó não visitado, vamos primeiro para o caminho mais curto. Este processo é repetido até que todos os nós tenham sido visitados e a distância do nó de origem seja calculada.
Implementação do algoritmo de Dijkstra usando uma pilha
É hora de implementar algum código para o algoritmo de Dijkstra em Python e veja como isso funciona. Começaremos usando uma implementação simples de uma fila de prioridade, conhecida como heap. O código pode ser representado da seguinte forma:
import heapq import sys def dijkstra_heap(adj_matrix, source): num_vertices=len(adj_matrix) distances=[sys.maxsize] * num_vertices distances[source]=0 visited=[False] * num_vertices heap=[(0, source)] enquanto heap: current_distance, current_vertex=heapq.heappop(heap) visitou[current_vertex]=Verdadeiro para o vizinho_vertex no intervalo(num_vertices): peso=adj_matrix[current_vertex][neighbor_vertex] se não for visitado [neighbor_vertex] and weight !=0: distance=current_distance + weight if distance distances[neighbor_vertex]: distances[neighbor_vertex]=distance heapq.heappush(heap, (distance, vizinho_vertex)) return distances adj_matrix=[ [0, 2, 2 , 0, 0, 0], [2, 0, 2, 0, 0, 0], [2, 2, 0, 2, 2, 6], [0, 0, 2, 0, 2, 2], [0, 0, 2, 2, 0, 2], [0, 0, 6, 2, 2, 0] ] distâncias=dijkstra_heap(adj_matrix, 0) print(di stances)
Explicação do Código
Vamos detalhar este código passo a passo para entendermos o que está acontecendo.
Importando Módulos
Primeiramente, estamos importando os módulos “heapq” e “sys”. O primeiro módulo nos permite usar a estrutura de dados heap, enquanto o segundo nos permite usar o valor inteiro máximo. Isso é necessário porque estamos inicializando as distâncias dos vértices até o infinito.
Definindo o Algoritmo de Dijkstra
Em seguida, definimos “dijkstra_heap” como uma função com dois argumentos — “adj_matrix” e “ fonte”. Estes são uma representação do gráfico como uma matriz de adjacência e o índice do nó de origem, respectivamente.
Visitando os nós
Neste bloco, estamos calculando o número de vértices. Então, estamos inicializando as distâncias do vértice de origem para cada vértice de destino ao infinito, conforme mencionado anteriormente. A distância do nó de origem também é definida como zero.
Uma lista é então criada, chamada “visited,” que é inicializada como “False.” Isso significa que os nós são inicialmente considerados não visitados até que tenhamos calculado a distância entre eles e a fonte. Uma fila de prioridade, chamada “heap”, também é criada, com o vértice inicial e a distância do nó de origem designados como uma tupla.
Atualizando os comprimentos de caminho mais curtos
Em seguida, nós tem um loop “while” que é executado até que a fila esteja vazia. A primeira linha pega o vértice da pilha que tem a distância mais curta do vértice de origem, e a segunda linha marca o vértice como visitado uma vez que essa distância é calculada.
Seguimos isso com um loop”for”, que itera sobre todos os vizinhos do vértice com o qual estamos preocupados. O peso de cada aresta é recuperado e se os nós vizinhos foram visitados, bem como se os pesos são diferentes de zero. A distância até o nó vizinho é então calculada usando a distância da fonte até o nó atual.
Temos outra instrução “if”, que verifica se a distância calculada é menor que a distância mais curta atual em nosso lista de “distâncias”. Nesse caso, a próxima linha atualiza esse valor. Por fim, o vértice vizinho, bem como sua distância da origem, é adicionado ao heap.
Saída de resultados
Após o término desse processo, as distâncias do nó de origem até todos os outros nós no gráfico são retornados ao console.
O penúltimo bloco de código simplesmente representa o gráfico que estamos vendo como uma matriz de adjacência, onde o valor na célula {i, j} representa o peso da borda que conecta os dois vértices.
O código final simplesmente informa ao sistema para calcular as distâncias de caminho mais curtas e, em seguida, imprimi-las no console.
Implementação do código
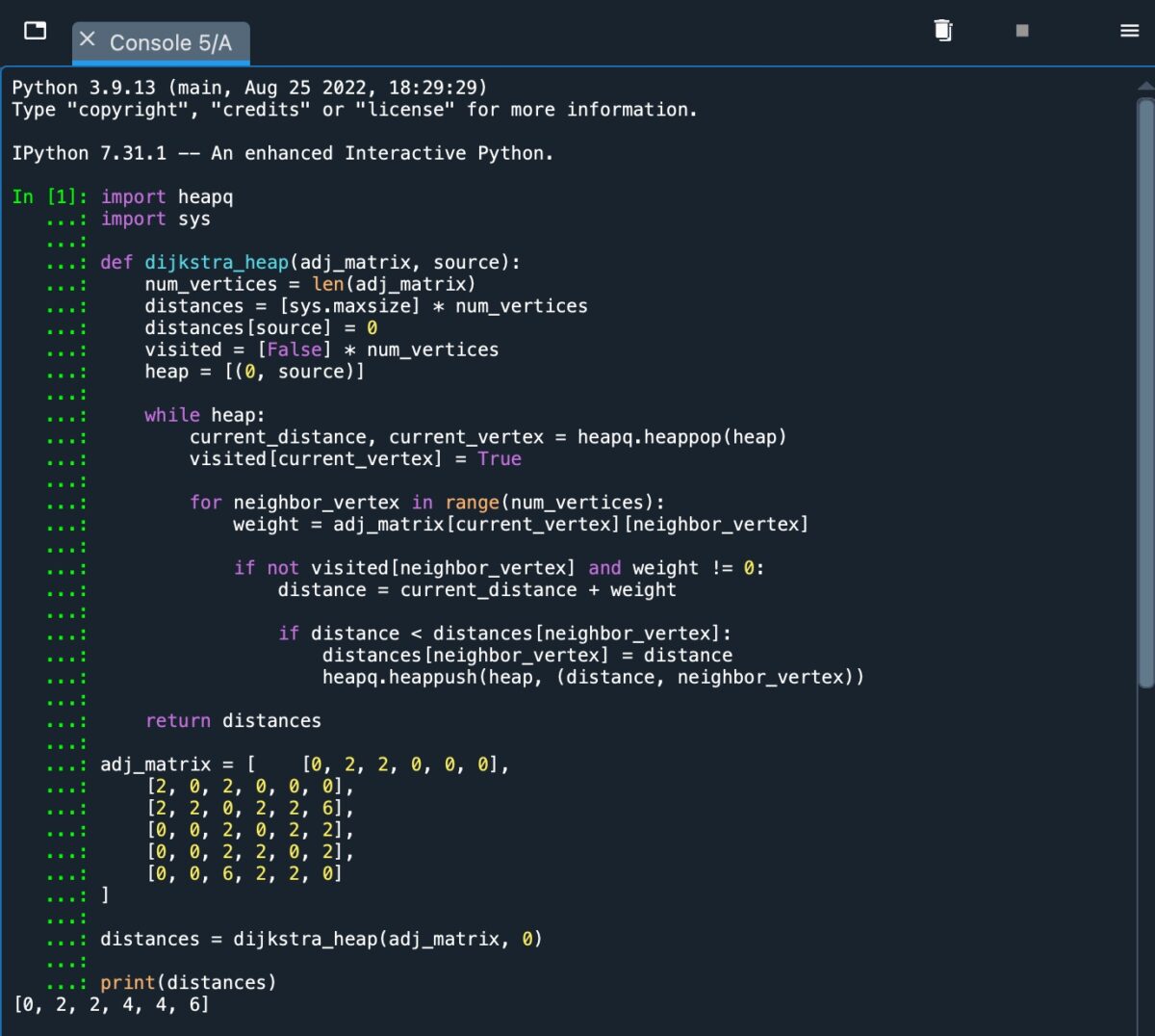 A implementação simples de um heap.
A implementação simples de um heap.
©”TNGD.com
Como podemos ver na captura de tela, recebemos uma saída de [0, 2, 2, 4, 4, 6], representando a menor distância do caminho do nó de origem A para os nós B, C, D, E e F.
Melhor e pior uso Casos do Algoritmo de Dijkstra
De uma forma geral, o algoritmo de Dijkstra é visto como eficiente, embora alguns algoritmos possam funcionar melhor em casos especializados. Com isso dito, vamos ver a complexidade de tempo e espaço do algoritmo de Dijkstra no melhor, médio e pior caso.
Complexidade de tempo do algoritmo de Dijkstra
Geralmente, temos apenas uma complexidade para cada caso. Mas, com o algoritmo de Dijkstra, a situação não é tão clara. Isso ocorre porque você pode implementar o algoritmo de diferentes maneiras, principalmente por meio do uso de uma fila de prioridade.
Ao usar uma fila de prioridade, você pode usar um método heap binário ou um método heap Fibonacci. Geralmente, o heap de Fibonacci leva a um desempenho mais eficiente e a uma melhor complexidade de tempo de pior caso de O((E + V) log V), onde E é o número de arestas e V é o número de vértices.
Se você não estiver usando uma fila de prioridade e o grafo for denso, a complexidade do pior caso pode ser tão ineficiente quanto O(V2 log V).
Em relação ao caso médio , a complexidade de tempo é um pouco mais favorável. O caso médio refere-se a quando uma fila de prioridade é usada para calcular as distâncias mínimas para cada vértice.
O melhor caso, em termos estritos, é incomum. Você provavelmente não se incomodaria em usar o algoritmo para resolvê-lo. Isso ocorre porque o melhor caso seria onde o vértice de origem é o mesmo que o vértice de destino. Isso significa que a iteração termina após apenas um loop.
A complexidade é, de facto, idêntica ao caso médio. Mas como os valores de E e V são iguais a 1, isso é simplificado para O(1). Se você estiver usando um heap para implementar seu algoritmo, a complexidade do melhor caso mudará para O(E* log V). Isso ocorre porque haverá no máximo O(E) vértices em sua fila.
Complexidade espacial do algoritmo de Dijkstra
Assim como a complexidade de tempo, a complexidade de espaço do algoritmo depende de sua implementação. Se você estiver usando uma lista de adjacência para representar seu gráfico e uma pilha de Fibonacci ou pilha regular, a complexidade será igual a O(V+E). Isso ocorre porque a distância do vértice da origem, bem como as arestas entre os vértices, precisam ser armazenadas na memória.
No entanto, se você usar uma matriz de adjacência, a complexidade será reduzida para O( V2). Isso ocorre porque você precisa armazenar as distâncias dos vértices, bem como uma matriz V * V para representar as arestas.
Resumindo
Para resumir, o algoritmo de Dijkstra é um dos muitos algoritmos usados para calcular os comprimentos de caminho mais curtos em um gráfico e é muito útil. Embora existam muitas maneiras de implementar o algoritmo, usar uma fila de prioridade de alguma descrição geralmente é sua melhor aposta.
Desses métodos, usar uma pilha de Fibonacci tende a ser o mais eficiente, particularmente para gráficos grandes. No entanto, para gráficos menores, uma fila de prioridade mais simples pode ser mais do que suficiente.
A seguir
Explicação do algoritmo de caminho mais curto de Dijkstra, com exemplos Perguntas frequentes (perguntas frequentes)
O que é o algoritmo de Dijkstra?
O algoritmo é usado para calcular os comprimentos de caminho mais curtos entre os nós em um grafo. É um método iterativo que começa com a distância mais curta do nó de origem e atualiza a distância para os nós vizinhos à medida que avança.
Quais são as limitações do algoritmo de Dijkstra?
O algoritmo não pode lidar com arestas de peso negativo, o que resultará em resultados incorretos.
Qual é a complexidade de tempo do algoritmo de Dijkstra?
A complexidade do tempo depende se você está usando uma fila de prioridade e como está implementando isso. No melhor caso, onde apenas uma iteração é necessária, a complexidade é O(1).
Caso contrário, o melhor caso é O(E* log V) ou O(E + V log V) , dependendo se você está usando um heap padrão ou um heap de Fibonacci.
Em ambos os casos, as complexidades para os casos médio e pior são as mesmas. O pior caso pode ser equivalente a O(V2 log V) se você não estiver usando uma fila de prioridade.
Qual é a complexidade espacial do algoritmo de Dijkstra?
Depende da implementação, mas pode ser em qualquer lugar de O(V2) a O(V + E).
Você pode usar o algoritmo de Dijkstra em um grafo que tem ciclos?
Sim, desde que nenhuma aresta de ponderação seja negativa.
Quais são as diferentes formas de implementar o algoritmo de Dijkstra?
Você pode usar uma fila de prioridade, como um heap ou um heap de Fibonacci. Geralmente, uma pilha de Fibonacci leva a resultados mais eficientes com gráficos maiores.
Quais são as alternativas ao algoritmo de Dijkstra?
Outros algoritmos de caminho mais curto incluem o A * algoritmo, algoritmo Bellman-Ford e algoritmo Floyd-Warshall. A* tende a ser mais rápido, mas requer mais memória.
Bellman-Ford e Floyd-Warshall podem lidar com arestas de peso negativo ao contrário de Dijkstra, mas ambos são mais ineficientes do que Dijkstra-eles têm complexidades de tempo de O(VE ) e O(V3) respectivamente.