© TippaPatt/Shutterstock.com
Cientistas da computação costumam usar gráficos para representar dados. Os gráficos podem representar vários relacionamentos, desde mapas e compostos químicos até relacionamentos sociais e redes de computadores. Podemos usar muitos algoritmos com gráficos, como o algoritmo de Dijkstra, o Depth-First Search (DFS) e o algoritmo Breadth-First Search (ou BFS). Embora você possa usar ambos os algoritmos para percorrer os nós de um grafo, o BFS é melhor para grafos não ponderados. Neste artigo, vamos explorar como o BFS funciona e suas aplicações.
O que é BFS?
BFS é um algoritmo de busca. O algoritmo inicia sua travessia no nó de origem e depois visita os nós vizinhos. Depois disso, o algoritmo escolhe o nó mais próximo no próximo nível de profundidade e então visita os nós inexplorados próximos a este, e assim por diante. Como o algoritmo BFS visita os nós em cada nível antes de passar para o próximo nível, é daí que vem o nome “Breadth-first”. Garantimos que visitamos cada nó apenas uma vez, rastreando os nós visitados e não visitados. Você pode usar o BFS para calcular distâncias de caminho, assim como com o algoritmo de Dijkstra.
O algoritmo por trás do BFS
Podemos representar o algoritmo básico com o seguinte pseudocódigo:
BFS(graph, start): fila=[start] visitado=set(start) enquanto a fila não está vazia: node=dequeue(queue) process(node) para o vizinho no gráfico.vizinhos(nó): se o vizinho não estiver visitado: visitado.add(vizinho) enqueue(fila, vizinho)
Neste caso, estamos definindo um gráfico como “grafo” e “início” é o nó inicial.
Implementamos uma estrutura de fila para armazenar os nós não visitados , bem como um conjunto “visited” para armazenar os nós visitados.
O loop “while” continua até que a fila esteja vazia e inicia o processamento dos nós nível por nível. A função “dequeue” remove o primeiro nó da fila conforme ele está sendo visitado.
A função “process” executa alguma função desejada no nó, como atualizar a distância para seus vizinhos ou imprimir dados para o console.
O loop “for” itera sobre todos os vizinhos do nó atual, verificando se o nó já foi visitado. Caso contrário, ele é adicionado à fila usando a função “enfileirar”. Em essência, os nós em cada nível são armazenados na fila, com seus vizinhos adicionados para serem visitados no próximo nível de profundidade. Isso nos permite determinar o caminho mais curto entre o nó de origem e todos os outros nós no gráfico.
O funcionamento do BFS
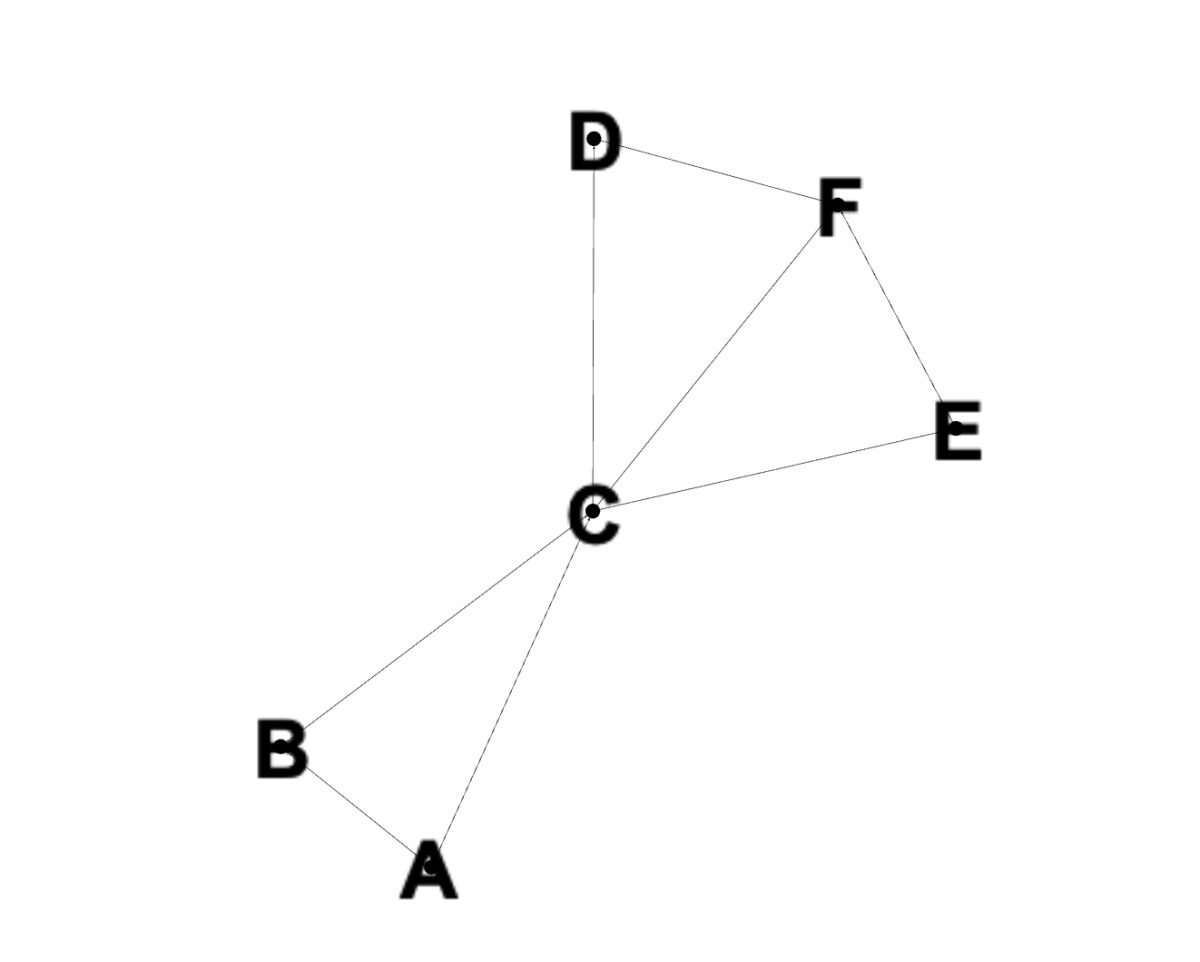Usaremos este gráfico para os seguintes exemplos de código.
©”TNGD.com
Com o básico explicado, é hora de ver como o BFS funciona na prática. Vamos ilustrar isso usando um grafo com os nós A, B, C, D, E e F, como mostra a imagem. O código abaixo mostra como implementar BFS para este gráfico usando a linguagem de programação Python.
from collections import defaultdict, deque def bfs(graph, start): queue=deque([start]) visited=set([start] ) while fila: node=queue.popleft() print(node) for vizinho in graph[node]: se o vizinho não estiver visitado: visited.add(neighbor) queue.append(neighbor) graph=defaultdict(list) edge=[ (“A”,”B”),”A”,”C”), (“B”,”C”), (“C”,”D”), (“C”,”E”), (“C”,”F”), (“D”,”F”), (“E”,”F”) para aresta nas arestas: graph[edge[0]].append(edge[0]) graph[ edge[1]].append(edge[0]) bfs(graph,”A”)
Explicação do Código
Primeiro, estamos importando as classes “defaultdict” e “deque” do módulo “coleções”. Eles são usados para criar um dicionário com valores de chave padrão e para criar uma fila que permite adicionar e remover elementos.
Em seguida, estamos definindo a função “bfs” com dois argumentos, “graph” e”começar”. Tomamos o argumento “grafo” como um dicionário com os vértices como chaves e os vértices vizinhos como valores. Aqui, “start” refere-se ao nó de origem, onde o algoritmo começa.
“queue=deque([start])” cria uma fila com o nó de origem como único elemento e “visited=set ([start])” cria um conjunto de nós visitados com o nó de origem como único elemento.
O loop “while” continua até que a fila esteja vazia. “node=queue.popleft()” remove o elemento mais à esquerda da fila e o armazena na variável “node”. “print(node)” imprime esses valores de nó.
O loop “for” itera sobre cada nó vizinho. “se vizinho não visitado” verifica se o vizinho foi visitado. “visited.add(neighbor)” adiciona o vizinho à lista visitada e “queue.append(neighbor)” adiciona o vizinho à extremidade direita da fila.
Depois disso, criamos um padrão dicionário chamado “grafo” e definir as arestas do grafo. O loop “for” itera sobre cada aresta. “graph[edge[0]].append(edge[1])” adiciona o segundo elemento da aresta como vizinho do primeiro elemento e o primeiro elemento da aresta como vizinho do segundo. Isso constrói o gráfico.
Finalmente, chamamos a função “bfs” em “grafo”, com o nó de origem como “A”.
Implementação do código
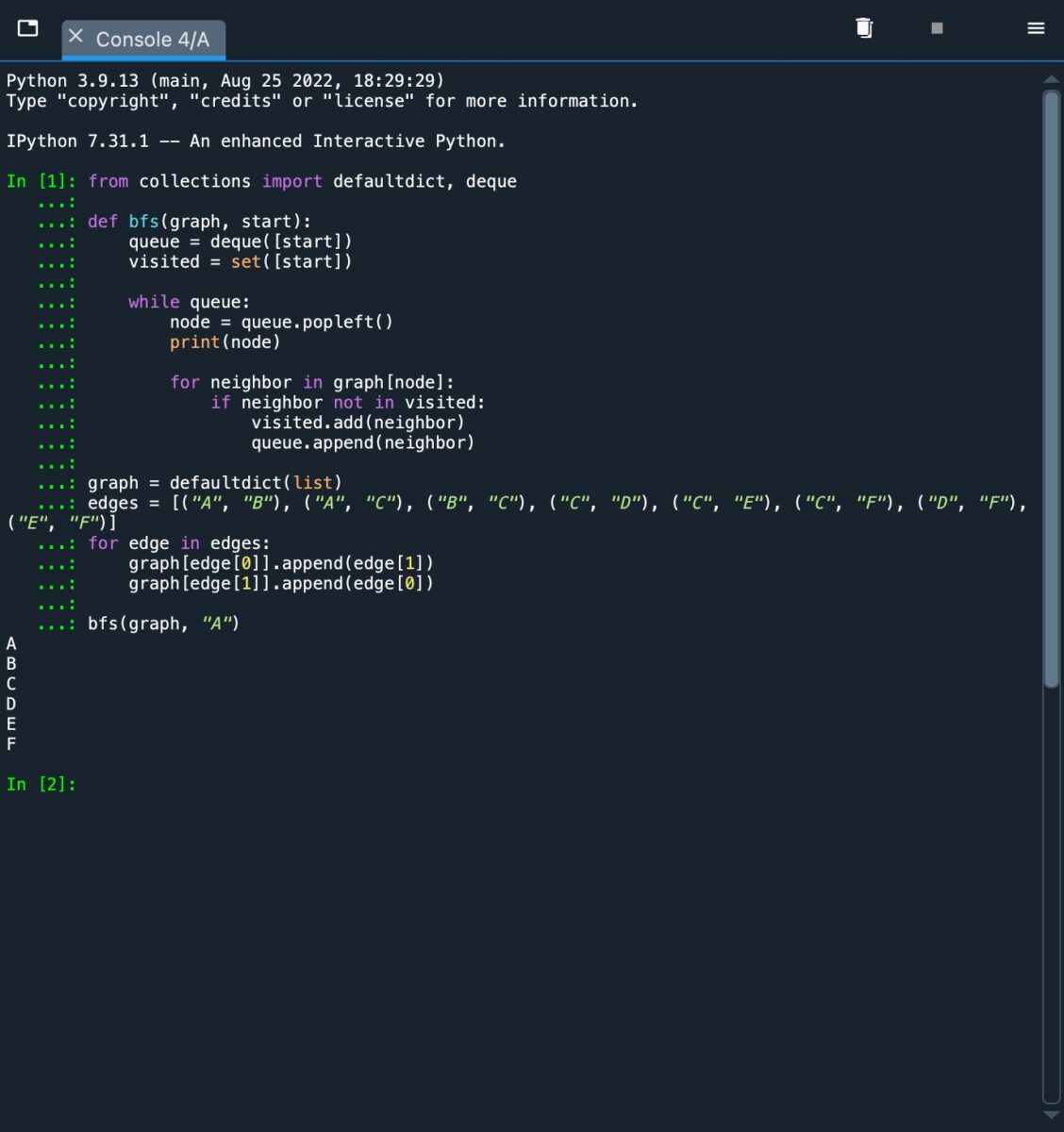É assim que o algoritmo BFS se parece quando implementado e executado através de um gráfico conectado.
©”TNGD.com
Na captura de tela, podemos ver a saída [A, B, C, D, E F]. Isso é o que esperávamos, pois o BFS explora os nós em cada nível de profundidade antes de passar para o próximo. Voltando ao gráfico, vemos que B e C serão adicionados à fila e visitados primeiro. B é visitado e, em seguida, A e C são adicionados à fila. Como A já foi visitado, C é visitado em seguida e A é removido. Depois disso, os vizinhos de C, D, E e F, são adicionados à fila. Estes são então visitados e a saída é impressa.
Usando BFS para gráficos desconectados
Usamos BFS para um gráfico conectado anteriormente. No entanto, também podemos usar o BFS quando os nós não estiverem todos conectados. Vamos usar os mesmos dados do gráfico, pois o algoritmo modificado pode ser ilustrado com qualquer tipo de gráfico. O código modificado é:
from collections import defaultdict, deque def bfs(graph, start): queue=deque([start]) visited=set([start]) while queue: node=queue.popleft() print (nó) para o vizinho no gráfico[nó]: se o vizinho não for visitado: visitado.add(vizinho) queue.append(vizinho) para o nó no gráfico.keys(): se o nó não for visitado: queue=deque([nó ]) visited.add(node) while queue: node=queue.popleft() print(node) for vizinho in graph[node]: se vizinho não estiver visitado: visited.add(neighbor) queue.append(neighbor) graph=defaultdict(lista) arestas=[(“A”,”B”), (“A”,”C”), (“B”,”C”), (“C”,”D”), (“C”,”E”), (“C”,”F”), (“D”,”F”), (“E”,”F”)] para borda em bordas: gráfico[borda[0]]. append(borda[1]) gráfico[borda[1]].append(borda[0]) bfs(graph,”A”)
Usamos um loop “for” adicional. O loop itera sobre todos os nós usando o método “graph.keys()”. O BFS inicia uma nova fila se encontrar um nó não visitado e funciona recursivamente. Ao fazer isso, visitamos todos os nós desconectados. Veja a imagem abaixo para uma ilustração.
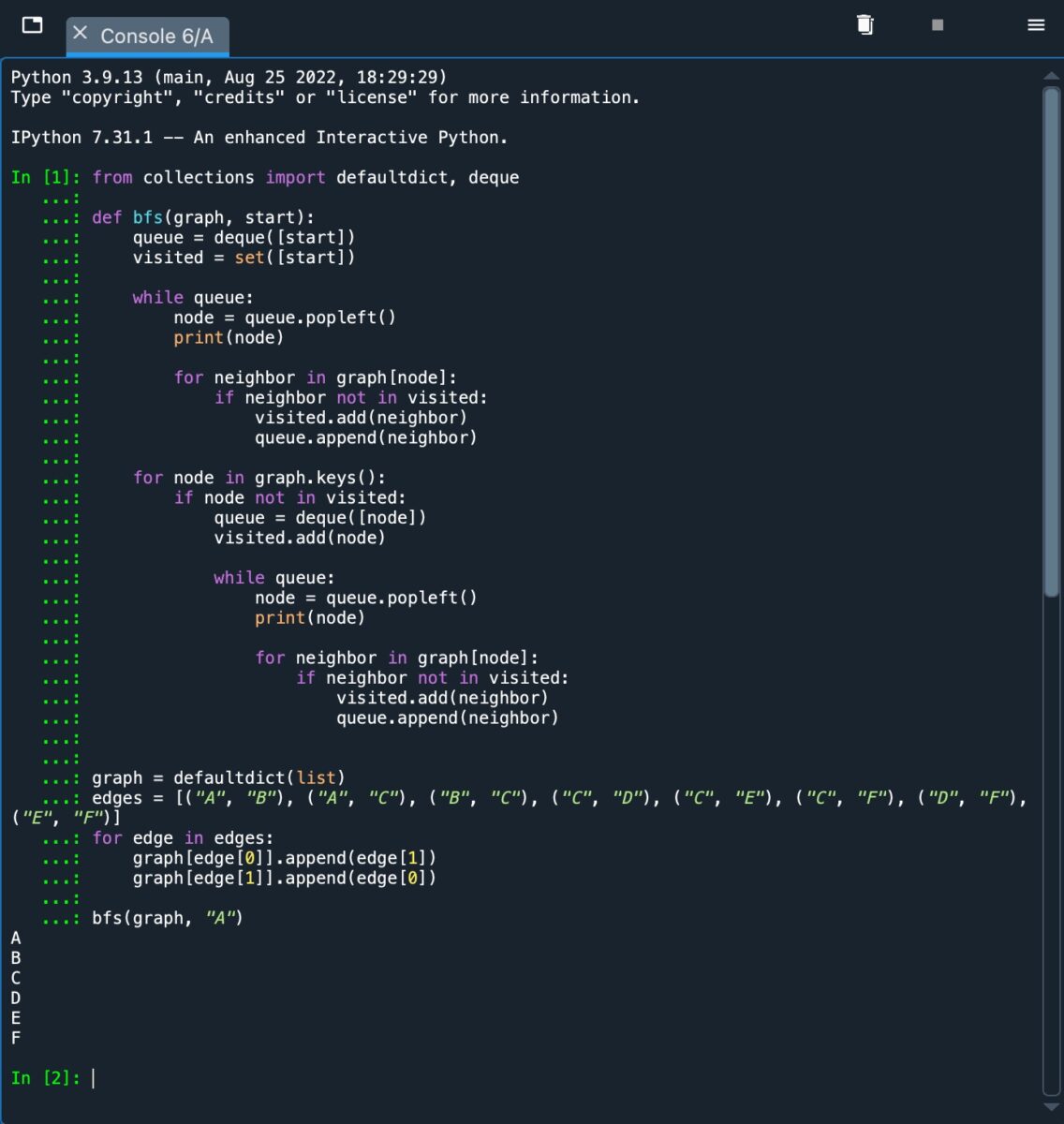Este é um exemplo do algoritmo BFS quando implementado e executado através de um grafo desconectado.
©”TNGD.com
Melhores e piores casos de uso para BFS
Agora que sabemos como o BFS funciona, devemos observar a complexidade de tempo e espaço do algoritmo para ter uma ideia de seus melhores e piores casos de uso.
Complexidade de tempo do BFS
Podemos ver que a complexidade de tempo é a mesma em todos os casos, e é igual a O(V + E), onde V é o número de vértices e E é o número de arestas. No melhor caso, onde temos apenas um nó, a complexidade será O(1), pois V=1 e E=0. No caso médio e pior, o algoritmo visita todos os nós que consegue alcançar a partir do nó de origem , então a complexidade depende da estrutura e tamanho do grafo em ambos os casos.
Complexidade espacial de BFS
Novamente, vemos que a complexidade é a mesma para todos os casos. O algoritmo visita cada nó independente da estrutura do grafo. Portanto, a complexidade depende do número de vértices no gráfico.
Resumo
BFS é uma maneira de percorrer os nós em um gráfico, calcular distâncias de caminho e explorar relações entre nós. É um algoritmo muito útil para explorar sistemas de rede e detectar ciclos de grafos. O BFS é relativamente fácil de implementar para grafos conectados e desconectados. Um benefício é que a complexidade de tempo e espaço é a mesma para todos os casos.
Pesquisa em largura (BFS) para gráficos – explicada, com exemplos Perguntas frequentes (perguntas frequentes)
O que é BFS?
BFS é um algoritmo usado para percorrer árvores ou grafos, geralmente aqueles que representam redes sociais ou redes de computadores. Ele também pode detectar ciclos de gráfico ou se um gráfico é bipartido, bem como calcular as distâncias de caminho mais curto. Largura primeiro significa que cada nó é explorado em um determinado nível de profundidade antes de passar para o próximo.
Qual é a complexidade de tempo do BFS?
O a complexidade de tempo do BFS é O(V + E) em todos os casos.
Qual é a complexidade do espaço do BFS?
A complexidade do espaço do BFS é O(V) em todos os casos.
Quando você deve usar o BFS?
Se você precisar calcular a distância do caminho mais curto ou explorar todos os vértices em um gráfico não ponderado.
Como o BFS é implementado?
Normalmente implementamos o BFS usando uma estrutura de dados de fila e um conjunto para acompanhar os nós visitados e não visitados. O nó de origem é adicionado à fila e marcado como visitado. Em seguida, o algoritmo opera recursivamente em nós vizinhos, adicionando e removendo nós à medida que avança para garantir que nenhum nó seja visitado duas vezes.
Como o BFS se compara ao algoritmo de Dijkstra?
Esses algoritmos podem ser usados para calcular as distâncias de caminho mais curto, mas o BFS funciona com gráficos não ponderados. Em contraste, o algoritmo de Dijkstra funciona com grafos ponderados.
Como o DFS se compara ao BFS?
Ambos são usados para percorrer um grafo, mas diferem em como eles fazem isso. Enquanto o BFS procura cada nó em um determinado nível de profundidade antes de prosseguir, o DFS visita os nós o mais profundamente possível antes de voltar para si mesmo para explorar outro ramo. O DFS geralmente usa uma estrutura de dados de pilha em vez de uma fila.