© Song_about_summer/Shutterstock.com
Ao pesquisar em gráficos ou estruturas de dados em árvore, dois algoritmos populares são a pesquisa em profundidade (DFS) e a pesquisa em largura (BFS). Ambos servem ao mesmo propósito de encontrar um caminho ou percorrer um grafo; no entanto, DFS vs. BFS diferem em termos de abordagem e eficiência.
O DFS é recursivo, percorrendo profundamente o gráfico e retrocedendo ao chegar a becos sem saída, enquanto o BFS visita iterativamente todos os nós adjacentes antes de avançar. Este artigo irá comparar DFS e BFS descrevendo as principais diferenças, bem como os prós e contras associados a cada abordagem.

DFS vs. BFS: comparação lado a lado
DFS x BFS: qual é a diferença?
À primeira vista, pesquisa em largura (BFS) e pesquisa em profundidade ( DFS) parecem semelhantes. O BFS percorre de acordo com a largura da árvore, enquanto o DFS segue a profundidade. Ambos compartilham um objetivo comum: pesquisar em grafos para localizar um nó ou caminho individual. Portanto, as principais diferenças entre eles serão discutidas mais abaixo.
Approach and Traversal Order
DFS (Depth First Search) e BFS (Breadth First Search) são dois algoritmos amplamente usados para percorrer grafos e árvores. Ambos os algoritmos visitam cada nó ou vértice do grafo ou árvore; no entanto, sua ordem de travessia e abordagem varia.
O DFS adota uma abordagem de profundidade, atravessando cada ramificação sucessivamente até atingir a profundidade de cada uma. Em outras palavras, ele explora o máximo possível ao longo de cada ramificação antes de retroceder. A ordem de passagem usada pelo DFS é LIFO (Last In First Out), o que significa que ele usa uma estrutura de dados de pilha para armazenar os nós visitados.
Por outro lado, o BFS adota uma abordagem de largura primeiro; ele visita todos os nós na profundidade atual antes de passar para aqueles em uma profundidade mais profunda. Ou seja, ele analisa todos os nós em cada nível antes de prosseguir para baixo. Além disso, sua ordem de passagem é FIFO (First In First Out), que utiliza uma estrutura de dados de fila para armazenar os nós visitados.
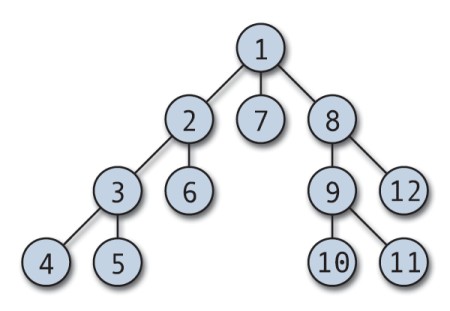 O algoritmo DFS procurará o mais longe possível em cada ramificação antes de retroceder.
O algoritmo DFS procurará o mais longe possível em cada ramificação antes de retroceder.
©Wolfram Esser/CC BY-SA 3.0 – Licença
Complexidade de tempo e espaço
Outra diferença significativa entre DFS e BFS é sua complexidade de tempo e espaço. A complexidade de tempo do DFS é O(V+E), onde V é o número de vértices e E é a contagem de arestas em um grafo ou árvore. Além disso, sua complexidade de espaço também excede O(V+E), pois todos os nós visitados devem ser armazenados em uma pilha até atingirem suas respectivas folhas.
Contrariamente, o BFS tem uma complexidade de tempo de O(V+E) , semelhante ao DFS; no entanto, sua complexidade espacial é O(V), pois armazena todos os nós visitados em um array. Portanto, o BFS pode exigir mais memória do que o DFS ao lidar com gráficos ou árvores grandes.
Casos de uso e aplicativos
O DFS e o BFS têm usos e aplicativos distintos. O DFS é freqüentemente empregado quando o espaço de busca é grande e profundo, com o objetivo de explorar o máximo possível qualquer caminho antes de retroceder. Também pode ser benéfico ao tentar localizar uma solução em jogos ou quebra-cabeças onde a resposta pode estar localizada no fundo do espaço do quebra-cabeça.
O BFS, por outro lado, é frequentemente empregado ao pesquisar um grande e espaço de busca raso para identificar o caminho mais curto entre dois nós ou vértices. Ele também determina a distância mais próxima entre dois nós de rede ou localizações em um mapa geográfico.
Integridade e otimização
Os algoritmos de busca devem atender a dois requisitos essenciais: integridade e otimização. Completude refere-se a se o algoritmo pode garantir encontrar uma solução, caso exista, enquanto a otimização implica encontrar o caminho mais curto ou ideal para essa solução.
O DFS não é perfeito ou ideal, pois pode ficar preso em um loop infinito ou falha em encontrar o caminho mais curto. O DFS pode travar se um ciclo em seu gráfico ou árvore falhar ao rastrear os nós visitados. Além disso, o DFS pode encontrar caminhos abaixo do ideal para resolver problemas.
No entanto, o BFS é completo e ideal. Ele garante encontrar uma solução, se houver, bem como encontrar o caminho mais curto. Depois de explorar todos os nós em um nível de profundidade antes de passar para outro, o BFS garante encontrar o caminho mais curto. No entanto, o BFS pode demorar mais do que o DFS em alguns casos, especialmente ao lidar com gráficos ou árvores profundos ou estreitos.
Gerenciamento de memória
Outro fator crucial ao selecionar entre DFS e BFS é a memória gerenciamento. O gerenciamento de memória refere-se a como um algoritmo usa a memória e quanto espaço é necessário para armazenar os nós visitados.
O DFS usa uma pilha para armazenar os nós visitados, mas grandes espaços de pesquisa ou gráficos podem causar problemas. Nesses casos, o DFS pode ficar sem memória e não conseguir localizar uma solução ideal; grafos ou árvores densas requerem mais memória devido aos ciclos frequentes.
O BFS conta com uma estrutura de dados de fila para armazenar os nós visitados, garantindo que não fique sem memória. No entanto, em certas circunstâncias, o BFS pode usar mais memória do que o DFS, especialmente quando o gráfico ou a árvore é amplo e raso ou possui muitos ramos. O BFS também pode exigir mais recursos se houver muitos nós ou se a estrutura for esparsa.
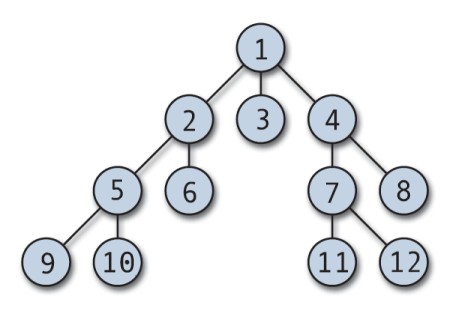 Um algoritmo BFS pesquisa todos os nós em uma profundidade antes de passar para os nós na próxima profundidade.
Um algoritmo BFS pesquisa todos os nós em uma profundidade antes de passar para os nós na próxima profundidade.
©Alexander Drichel/CC BY-SA 3.0 – Licença
Complexidade de implementação
A complexidade de implementação de um algoritmo refere-se a quão fácil ou difícil é executá-lo. Isso depende da linguagem de programação usada, das estruturas de dados disponíveis e de qualquer lógica necessária para a conclusão bem-sucedida.
O DFS geralmente é mais fácil de implementar do que o BFS, pois precisa apenas de uma estrutura de dados de pilha e função ou loop recursivo. O DFS pode ser implementado usando um algoritmo fácil de busca em profundidade que visita cada nó antes de explorar cada ramificação por vez. Além disso, é mais simples de implementar em linguagens de programação recursivas, como Python, onde a recursão ocorre naturalmente.
BFS, em por outro lado, requer uma estrutura de dados de fila e loop. Para implementá-lo de forma eficiente, o BFS usa um algoritmo de busca em largura que visita todos os nós em uma profundidade antes de passar para a próxima. No entanto, implementar o BFS em linguagens de programação recursivas como Python pode ser mais desafiador, pois requer um loop real em vez de simplesmente recursão.
Aplicativos
DFS e BFS têm aplicativos distintos em vários domínios. O DFS é comumente empregado em computação gráfica, inteligência artificial e rastreamento da Web para oferecer modelos e imagens 3D explorando o espaço 3D para renderizar objetos. A inteligência artificial usa DFS para árvores de decisão ou árvores de jogos – avaliando cada movimento possível para explorar os galhos da árvore – enquanto web crawlers usam DFS para rastrear a web e explorar links em páginas.
O BFS tem sido amplamente utilizado em redes roteamento, algoritmos de caminho mais curto e quebra-cabeças. No roteamento de rede, ele encontra o caminho mais curto entre dois nós explorando todos os caminhos possíveis até encontrar o mais curto. O BFS também desempenha um papel nos algoritmos de caminho mais curto, como o de Dijkstra ou A*, que garante encontrar a rota mais curta; da mesma forma, ao resolver quebra-cabeças como o Cubo de Rubik usando BFS, você determina a solução mais curta que resolve o quebra-cabeça.
 Usar BFS para resolver o Cubo de Rubik determinará a solução mais rápida para resolver o quebra-cabeça.
Usar BFS para resolver o Cubo de Rubik determinará a solução mais rápida para resolver o quebra-cabeça.
©gd_project/Shutterstock.com
Espaço de busca
O espaço de busca é o conjunto de todos os estados ou configurações possíveis que um algoritmo pode explorar para encontrar sua solução. Pode ser representado como um grafo ou árvore, onde cada nó representa um estado ou configuração, e cada aresta significa uma transição entre eles.
O DFS investiga o espaço de busca de maneira profunda, explorando cada ramificação até onde quanto possível antes de voltar atrás e explorar outros ramos. Essa abordagem funciona melhor para espaços de pesquisa grandes e profundos, onde a solução pode estar bem dentro dele. Infelizmente, o DFS pode ficar preso em um loop infinito se um loop infinito estiver presente e não acompanhar os nós visitados.
O BFS percorre o espaço de pesquisa em largura, explorando todos os nós de uma só vez profundidade antes de prosseguir para a próxima. É ideal para espaços de busca grandes ou rasos onde a solução pode estar próxima da raiz. O BFS garante encontrar o caminho mais curto para essa solução, mas pode ocupar mais memória e ser mais lento em alguns casos do que o DFS.
Estratégia de pesquisa
Uma estratégia de pesquisa refere-se a um algoritmo que decide qual nó para explorar a seguir. Fatores como custo, heurística ou aleatoriedade podem orientar esse processo de tomada de decisão.
O DFS emprega uma estratégia de busca em profundidade, na qual explora cada ramificação o máximo possível antes de retornar e explorar outras ramificações. O DFS não usa nenhum custo ou heurística ao selecionar qual nó explorar a seguir; assim, pode explorar caminhos abaixo do ideal. Em certos casos, o DFS também pode depender da aleatoriedade, como Monte Carlo Tree Search.
O BFS geralmente usa uma estratégia de busca em largura, explorando todos os nós em uma profundidade antes de prosseguir para a próxima. Por outro lado, emprega uma estratégia de busca de custo uniforme que prioriza os nós com o menor custo. Em certos casos, o BFS também pode contar com heurísticas como o algoritmo A*, que utiliza custo e distância estimada para decidir qual nó explorar em seguida.
DFS vs. BFS: 10 fatos que você deve saber
DFS significa Depth First Search, enquanto BFS significa Breadth First Search.DFS atravessa um grafo ou árvore em um movimento de profundidade, enquanto BFS se move de acordo com a largura da árvore. Para acompanhar os nós visitados durante a travessia DFS, eles usam uma pilha, enquanto com BFS, ele usa uma fila. O DFS pode ser empregado para classificação topológica, detecção de ciclo e localização de componentes fortemente conectados em grafos; enquanto o BFS procura encontrar o caminho mais curto entre dois nós. O DFS ocupa menos espaço, enquanto o BFS requer mais, pois armazena todos os nós no nível atual antes de prosseguir para o próximo. O DFS é mais rápido ao resolver problemas que envolvem um grande número de nós, enquanto o BFS se destaca ao lidar com grupos menores. O DFS percorre todos os nós em um grafo ou árvore, enquanto o BFS visita apenas aqueles ao longo do caminho mais curto. O DFS usa uma estratégia de pesquisa em profundidade, enquanto o BFS emprega uma abordagem em largura. O DFS pode não encontre o caminho mais curto, enquanto o BFS sempre o faz. Além disso, o DFS pode ficar preso em um loop infinito se o gráfico contiver ciclos; no entanto, o BFS sempre termina quando restam apenas nós finitos.
DFS vs. BFS: qual é o melhor?
Os algoritmos de busca em profundidade (DFS) e busca em largura (BFS) possuem suas próprias vantagens e desvantagens específicas, tornando-os mais adequados para certos cenários do que o outro.
O DFS percorre eficientemente grafos profundos ou infinitos com baixa complexidade de espaço e implementação baseada em recursão. Ele também detecta efetivamente os ciclos em um gráfico, uma vez que explora o máximo ao longo de cada ramificação antes de retroceder. O DFS fornece soluções para problemas como encontrar componentes conectados, classificação topológica e o quebra-cabeça de 8; modificações são possíveis.
Por outro lado, o BFS é mais adequado para encontrar o caminho mais curto entre dois nós em um grafo, pois examina todos os nós nessa profundidade antes de passar para o próximo nível. Além disso, pode ser empregado para calcular a árvore geradora mínima de um grafo e resolver problemas como o Knight’s Tour.
Ambos os algoritmos têm suas próprias complexidades de tempo, e a escolha entre eles depende do problema específico e características do gráfico que está sendo analisado. De um modo geral, o BFS tem uma complexidade de tempo maior que o DFS, mas garante o caminho mais curto entre dois nós em um grafo não ponderado; por outro lado, DFS pode ter menor complexidade, mas nem sempre pode garantir esse caminho mais curto.
Em conclusão, a escolha entre DFS vs. BFS depende do problema que está sendo resolvido e do grafo que está sendo analisado. Ambos os algoritmos têm seus pontos fortes e fracos; portanto, entender ambos pode ajudar a selecionar o mais adequado para um problema específico. Portanto, é essencial ter os dois tipos de algoritmos em sua caixa de ferramentas, juntamente com exemplos nos quais eles são mais úteis.
DFS x BFS: Comparação completa e 9 principais diferenças FAQs (perguntas frequentes)
Qual algoritmo é melhor para encontrar um caminho entre dois nós?
BFS e DFS podem ser empregados para encontrar um caminho entre dois nós. O BFS é melhor em encontrar a rota mais curta, enquanto o DFS prefere encontrar caminhos que podem não ser os mais curtos, mas podem ter outras características desejáveis, como ser de tipo topológico ou componente fortemente conectado.
Qual algoritmo é melhor para percorrer um grafo esparso?
O BFS é superior para percorrer um grafo esparso, pois explora todos os nós em um nível antes de prosseguir, tornando-o eficiente quando há poucas arestas. Pelo contrário, o DFS pode explorar muitos nós não relacionados, tornando-o menos eficiente ao trabalhar em grafos esparsos.
Qual algoritmo é melhor para percorrer um grafo denso?
DFS é mais eficiente ao percorrer um grafo denso, pois explora os nós em profundidade e pode retroceder rapidamente para aqueles ainda relevantes para a pesquisa. No entanto, o BFS pode sondar muitos nós irrelevantes de uma só vez antes de alcançar o nó desejado, tornando-o menos eficaz em redes densas.
O DFS e o BFS podem ser usados para localizar os componentes conectados de um grafo?
Sim, DFS e BFS podem ser empregados para descobrir os componentes conectados de um grafo. O DFS começa em um nó e percorre o máximo possível antes de retornar e explorar outros nós não visitados, enquanto o BFS examina todos os nós em um nível antes de avançar para o próximo.
O DFS e o BFS podem ser usados para detectar ciclos em um gráfico?
Sim, DFS e BFS podem ser usados para detectar ciclos em gráficos. O DFS detecta ciclos mantendo o controle dos nós visitados em uma lista e pilha de nós sendo explorados; se esse mesmo nó reaparecer sem ser seu pai em nenhuma ordem, será considerado um novo ciclo. Da mesma forma, o BFS mantém ambas as listas de nós visitados e uma fila ativa de nós sendo explorados; se um nó visitado anteriormente reaparecer sem ser seu próprio filho dentro desta última fila, ele será sinalizado como potencialmente prejudicial.
O DFS e o BFS podem ser usados para encontrar a classificação topológica de um grafo acíclico direcionado ( DAG)?
Sim, DFS e BFS podem ser empregados para determinar o tipo topológico de um DAG. Com o DFS, isso é feito mantendo um índice de nós visitados, bem como uma pilha contínua daqueles que estão sendo explorados. Uma vez que todos os filhos de cada nó tenham sido explorados, eles são adicionados à ordenação topológica; da mesma forma, no BFS, há também um índice que rastreia os nós visitados junto com uma fila em andamento que aguarda exploração; quando todos os pais de um nó foram explorados, ele também é incluído na classificação topológica.
O DFS e o BFS podem ser usados para encontrar o caminho mais curto em um grafo ponderado?
BFS pode ser empregado para encontrar o caminho mais curto em um grafo não ponderado, enquanto o algoritmo de Dijkstra é empregado para grafos ponderados. No entanto, o DFS também pode ser bem-sucedido quando os pesos não são negativos e a pesquisa é limitada a um componente conectado.