© whiteMocca/Shutterstock.com
Os algoritmos de classificação geralmente se enquadram em dois campos-fáceis de implementar ou mais rápidos de executar. A classificação rápida geralmente se enquadra na última categoria. Continue lendo para descobrir como implementar esse algoritmo e as melhores situações para usá-lo.
O que é Quick Sort?
Quick sort é um algoritmo de classificação usado para organizar matrizes de dados. Baseia-se essencialmente no princípio conhecido como dividir e conquistar. Este é o método pelo qual dividimos um problema maior e mais complexo em subproblemas mais simples. Esses subproblemas são resolvidos e as soluções são combinadas para encontrar a solução para o problema original.
O algoritmo por trás da classificação rápida
Isso não é exatamente como implementar a classificação rápida, mas dá uma ideia de como funciona.
//i-> Índice inicial, j–> Índice final Quicksort(array, i, j) { if (i j) { pIndex=Partition(A, i, j) Quicksor(A,i, pIndex-1) Quicksort(A,pIndex+1, end) } }
Primeiro, definimos a ordenação rápida como uma função de um array com um elemento inicial e um elemento final. A instrução “if” verifica se o array contém mais de um elemento.
Nesse caso, chamamos a função “partition”, que nos dá o índice do elemento “pivot”. Isso separa o array em dois subarrays, com elementos menores e maiores que o pivô, respectivamente.
A função é chamada recursivamente em cada subarray, até que cada subarray tenha apenas um elemento. A matriz classificada é retornada e o processo é concluído.
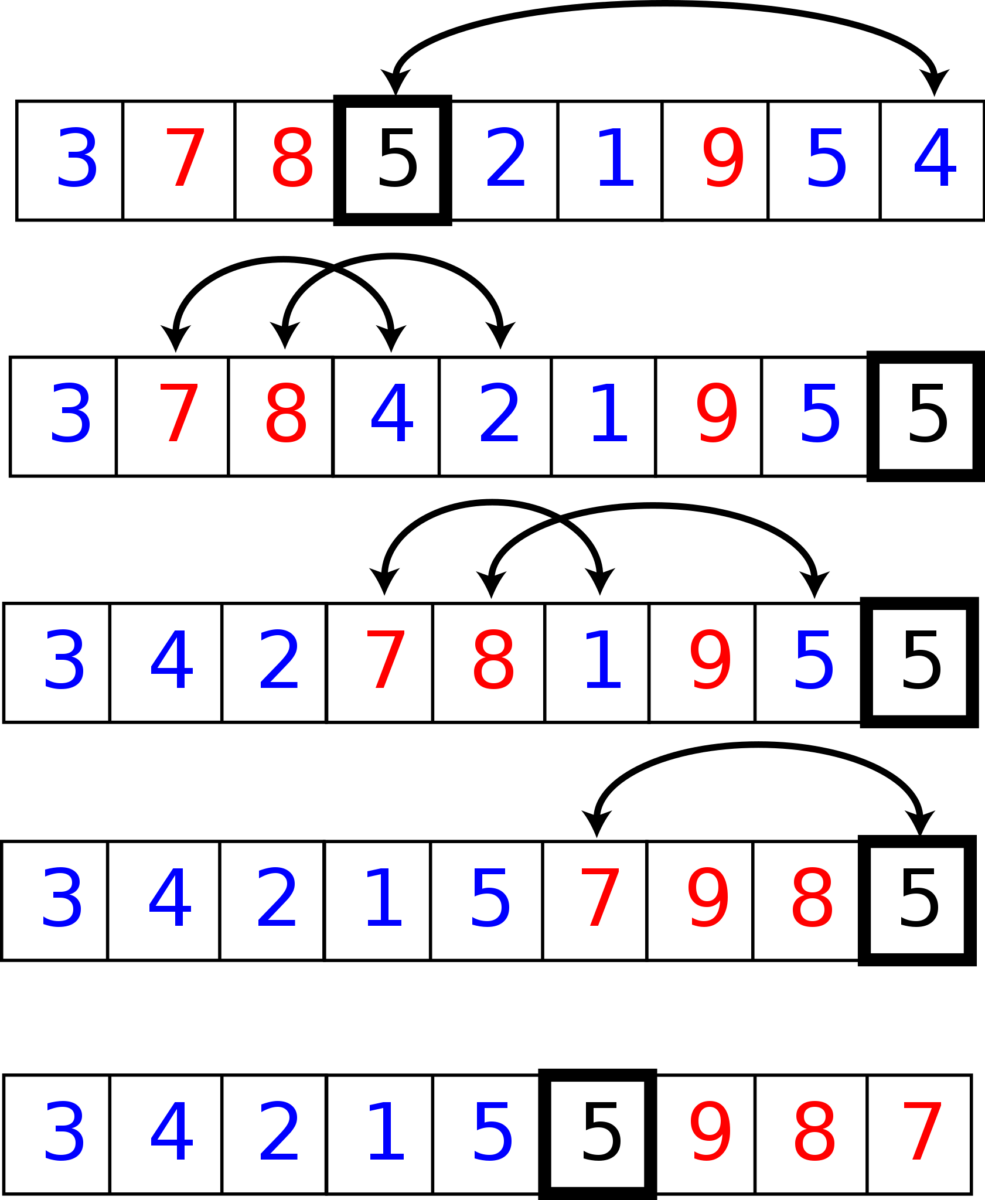Neste exemplo, o elemento em caixa é o elemento pivô, os elementos azuis são iguais ou menores e os elementos vermelhos são maiores.
©Dcoetzee/Public Domain – Licença
Um exemplo de classificação rápida
Como na maioria das coisas, rápido sort é melhor explicado usando um exemplo para ilustrar.
Vamos pegar o seguinte array – [56, 47, 98, 3, 6, 7, 11]
Temos índices de 0 a 6 (lembre-se de que o primeiro elemento é o índice 0, não 1).
Tomando o último elemento como o pivô, a matriz é reorganizada para que os elementos menores que o pivô fiquem à esquerda e elementos maiores estão à direita. Isso é feito inicializando as variáveis i e j como 0. Se arr[j], ou o elemento atual, for menor que o pivô, nós o trocamos por arr[i] e fazemos isso de forma incremental. O pivô é então trocado por arr[i] para que este elemento esteja em sua posição classificada.
Isso fornece os subarrays [6, 7, 3] e [56, 47, 98]. O índice do elemento pivô agora é 3 em vez de 6.
A classificação rápida é então chamada, que classifica o subarray esquerdo em torno do elemento pivô, 3, classificando os subarrays [6] e [7].
Em seguida, chamamos a classificação rápida recursivamente no subarray certo, de modo que seja classificado em [47, 56, 98].
Finalmente, os subarrays são combinados para fornecer o array classificado – [3, 6, 7, 11, 47, 56, 98].
Implementação
Agora que cobrimos a base por trás da classificação rápida, vamos implementá-la usando Python. O código que usamos pode ser descrito como:
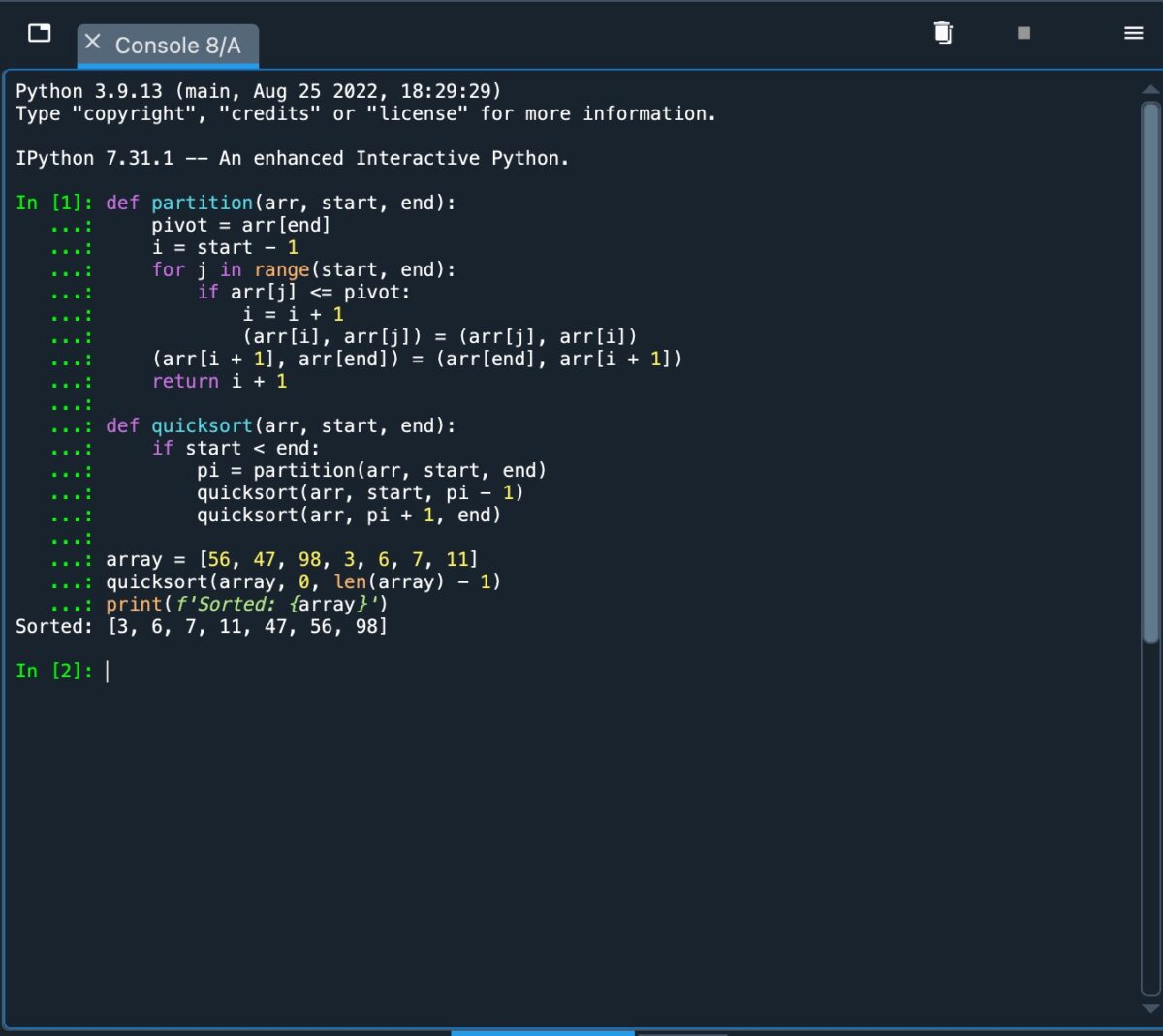
def partition(arr, start, end): pivot=arr[end] i=start-1 for j in range(start, end): if arr[j]=pivô: i=i + 1 (arr[i], arr[j]=(arr[j], arr[i]) (arr[i + 1], arr[end])=(arr[end], arr[i + 1]) return i + 1 def quicksort(arr, start, end): if start end: pi=partition(arr, start, end) quicksort(arr, start, pi-1) quicksort(arr, pi + 1, end) array=[56, 47, 98, 3, 6, 7, 11] quicksort(array, 0, len(array)-1) print(f’Sorted: {array}’)
Primeiro , estamos definindo uma função de partição como uma função de uma matriz, com um índice inicial e final.
O valor pivô é definido como o último elemento da matriz e i é inicializado como o início índice, menos 1.
O loop “for” itera sobre a matriz, do índice inicial ao índice final menos 1.
A instrução “if” troca o elemento atual, j, com o valor no índice i se j for menor que ou eq ual ao pivô. A variável i é então incrementada.
Depois disso, o pivô é trocado pelo elemento no índice i+1. Isso significa que todos os elementos à esquerda do pivô são menores ou iguais a ele e os elementos à direita são maiores que ele.
O índice do valor pivô é então retornado.
“Quicksort” é então definido como uma função do array, e o array é verificado para ter certeza de que tem mais de um elemento.
A função “partition” é então chamada, com o índice valor definido como “pi”. A classificação rápida é chamada recursivamente nos subarrays esquerdo e direito, até que cada subarray contenha apenas um elemento.
Finalmente, um array classificado é criado e impresso usando a função “print”.
A classificação rápida é chamada recursivamente à esquerda e subarrays à direita, até que cada subarray contenha apenas um elemento.
©”TNGD.com
Melhores e piores casos de uso de classificação rápida
Embora a teoria por trás da classificação rápida possa parecer complicado no início, o algoritmo tem muitas vantagens e geralmente é bastante rápido. Vamos dar uma olhada na complexidade de tempo e espaço da classificação rápida.
Complexidade de tempo da classificação rápida
A tabela resume a complexidade de tempo da classificação rápida.
O melhor caso é quando a partição é balanceada, onde o pivô é próximo ou igual ao valor mediano. Como tal, ambos os subarrays são de tamanho semelhante e n operações são executadas em cada nível. Isso leva a uma complexidade de tempo logarítmica.
Quando o elemento pivô está relativamente próximo, esse é o caso médio. A complexidade de tempo é a mesma do melhor caso, pois os arrays são aproximadamente iguais em tamanho.
No entanto, o pior caso transforma a complexidade de tempo em tempo quadrático. Isso ocorre porque o array é muito desbalanceado, onde o pivô está próximo do elemento mínimo ou máximo. Isso causa uma situação em que os subarrays são muito desiguais em tamanho, com um contendo apenas um elemento. Como tal, existem n níveis de recursão, bem como n operações, levando a uma dependência quadrática do tamanho da entrada.
Complexidade espacial da classificação rápida
Outro fator a considerar é o espaço complexidade de ordenação rápida. Isso pode ser resumido da seguinte forma:
A complexidade de espaço para classificação rápida é a mesma para o melhor e para o médio casos. Isso ocorre porque o algoritmo tem log n níveis recursivos e cada chamada recursiva usa uma quantidade constante de espaço de memória. Como tal, o espaço de memória total é proporcional à profundidade da árvore de recursão.
No pior caso, entretanto, a complexidade do espaço é alterada para O(n). Como a árvore de recursão é significativamente desbalanceada, o que significa que há n chamadas recursivas.
Resumo
No geral, a classificação rápida é, como o nome sugere, uma maneira muito eficiente de classificar um array, particularmente os grandes. Depois que o processo é compreendido, é relativamente fácil implementá-lo e modificá-lo. É útil em uma ampla variedade de cenários e funciona como uma boa base para algoritmos de classificação mais complexos.
A seguir…
O que é classificação rápida e como ela funciona? (Com exemplos) FAQs (Perguntas frequentes)
O que é classificação rápida?
A classificação rápida é um algoritmo de classificação para classificar matrizes de dados. Ele funciona selecionando um elemento pivô e particionando o array em dois subarrays, um com elementos menores que o pivô e outro com elementos maiores. Esse processo é repetido recursivamente até que cada subarray seja classificado e contenha apenas um elemento. As matrizes são então combinadas para fornecer uma matriz classificada.
A classificação rápida é um algoritmo estável?
A classificação rápida geralmente é um algoritmo instável. Isso significa que a ordem relativa de elementos iguais pode não ser preservada na saída final.
Como você escolhe o elemento pivô com classificação rápida?
Você pode escolher o primeiro ou o último elemento ou fazer uma escolha aleatória. Com conjuntos de dados especialmente grandes, randomizar a escolha geralmente leva a um bom desempenho.
Qual é a complexidade de tempo da classificação rápida?
O melhor caso e o médio é O(n log n), enquanto o pior caso é O(n2).
Qual é a complexidade espacial da ordenação rápida?
O melhor e os casos médios são O(log n), enquanto o pior caso é O(n).
Quais são os melhores casos para usar a ordenação rápida?
A classificação rápida pode ser usada para muitos tipos de arrays, mas, às vezes, alternativas como classificação por heap ou classificação por mesclagem podem funcionar melhor, dadas certas restrições. Normalmente, é aqui que você precisa de um algoritmo estável, como classificação por mesclagem, ou onde o tempo é um fator. Por exemplo, a complexidade de tempo do pior caso da classificação de heap é tão boa quanto a complexidade de tempo de caso média para classificação rápida. Algoritmos mais simples, como seleção ou classificação por inserção, também podem ser mais rápidos para pequenos conjuntos de dados.