© metamorworks/Shutterstock.com
Ao classificar uma matriz de dados, é crucial se familiarizar com os algoritmos de classificação. Nas estruturas de dados, a classificação é a organização dos dados em um formato específico com base em um relacionamento linear entre os itens de dados.
A classificação é essencial, pois a pesquisa de dados pode ser otimizada em um nível muito alto quando os dados são classificados em um determinado formato. Além disso, a classificação pode representar dados em um formato mais legível. Temos uma ampla variedade de algoritmos de classificação, mas neste artigo examinaremos o que é Heap sort e como usá-lo. Vamos direto ao assunto!

O que é Heap Sort: uma definição exata
Heap sort é um algoritmo de classificação bem conhecido e eficiente. É um conceito usado para classificar dados de array eliminando os elementos um por um da pilha-uma árvore binária completa-parte da lista e, em seguida, inserindo-os na parte classificada da lista.
Classificação de pilha basicamente tem duas fases envolvidas:
Criação de um heap, seja heap máximo ou heap mínimo, usando elementos de uma matriz especificada. Excluir recursivamente o elemento raiz do heap criado na primeira fase.
Como funciona o algoritmo de classificação de pilha?
Veja como o algoritmo de classificação de pilha é implementado:
Crie uma pilha máxima para armazenar dados da lista não classificada. Retire o maior valor de o heap e insira-o em uma lista classificada. Troque a raiz do heap com o último elemento da lista e, em seguida, rebalanceie o heap. Assim que o heap máximo estiver completamente vazio, retorne a lista classificada.
Aqui está o algoritmo
HeapSort(arr)
CreateMaxHeap(arr)
para i=length(arr) para 2
trocar arr[1] por arr[i]
heap_size[arr]=heap_size[arr] ? 1
MaxHeapify(arr,1)
End
Vamos examinar as etapas um pouco mais.
Etapa 1: criar um máximo-heap
CreateMaxHeap(arr)
heap_size(arr)=length(arr)
for i=length(arr)/2 a 1
MaxHeapify(arr,i)
End
Neste algoritmo, precisaremos construir um heap máximo. Como todos sabemos, em um heap máximo, o maior valor é o valor raiz. Cada nó pai precisa ter um valor maior que seus filhos associados.
Imagine que temos a lista abaixo de valores não classificados:
[14, 11, 2, 20, 3, 10 , 3]
Colocando nossos valores em uma estrutura de dados de pilha máxima, nossa lista ficaria assim:
[20, 11, 14, 2, 10, 5 , 3]
Podemos apresentar o heap máximo acima assim:
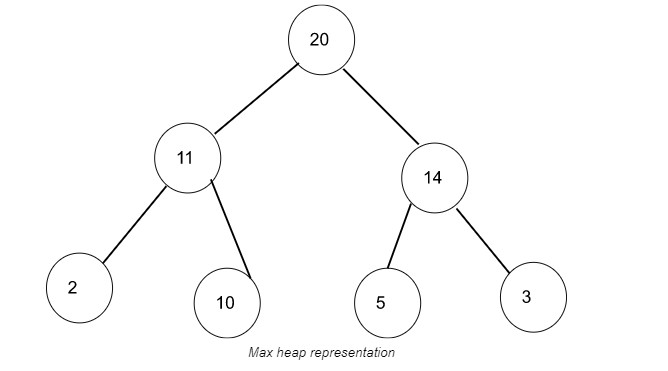 Apresentação de um heap máximo.
Apresentação de um heap máximo.
©”TNGD.com
Etapa 2: Retire a raiz do heap
Para classificar os dados, vamos extrair e eliminar repetidamente o maior valor da pilha até que esteja vazio. Se seguirmos os princípios dos heaps, podemos antecipar que o maior valor estará localizado na raiz do heap.
Depois de eliminar o maior valor, não podemos simplesmente abandonar o heap sem raiz, porque ele resultaria na desconexão de dois nós. Em vez disso, podemos trocar o nó raiz pelo último elemento da pilha. Como o último elemento não tem filhos, ele pode ser facilmente removido da pilha.
No entanto, esta etapa causa um grande problema. Ao trocar os dois elementos, o nó raiz agora não é o maior da pilha. O heap precisará ser reestruturado para garantir que esteja balanceado.
Etapa 3: Heapify down (restaurar o heap)
O valor da raiz não sendo o valor maior, o princípio do heap foi violado porque o pai deve ter um valor maior que o valor dos filhos.
No entanto, existe uma solução para este problema! Precisamos acumular, o que envolve adicionar um valor ao final do heap e subir na estrutura de dados até encontrar a posição apropriada. Para resumir, você compara o novo valor raiz com seus filhos, seleciona o filho com o maior valor e o troca pelo valor raiz. Desça a pilha até que esteja equilibrada.
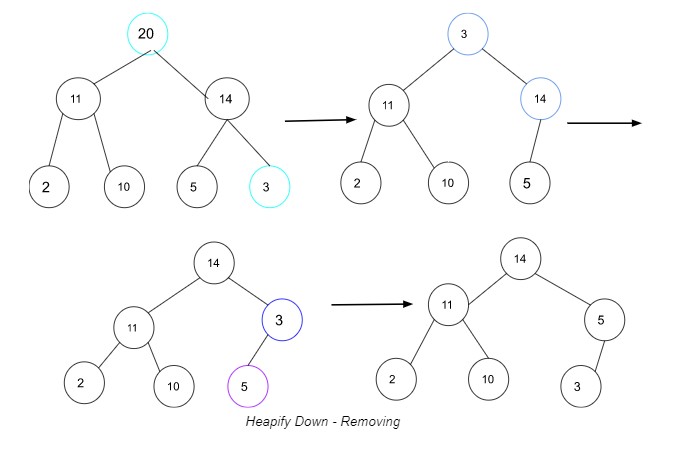 Ilustração do processo heapify down.
Ilustração do processo heapify down.
©”TNGD.com
No exemplo acima, você troca o valor raiz original 20 por 3 – o filho mais à direita. Tendo 3 como a nova raiz, compare seu valor com o valor filho 14 e, como é maior que 3, troque-os para fazer 14 a nova raiz. Em seguida, compare 3 com seu novo filho 5 e, como 5 é maior que 3, troque-os para que 5 seja o novo valor pai. Como não há outros filhos para comparar com 3, a pilha agora está balanceada.
Etapa 4: Repita
você precisará repetir o procedimento de troca da raiz e da última elemento, retirando o maior valor e reequilibrando o heap, desde que a estrutura de dados contenha um tamanho maior que 1. Quando esse critério for atendido, você terá um conjunto de valores classificados.
Complexidade de classificação de heap
Complexidade de tempo
Aqui está a complexidade de tempo do Heap Sort no melhor caso, caso médio e pior caso.
Best Case Complexity: Ocorre quando a matriz já está classificada, ou seja, nenhuma classificação é necessária. O(n log n) é a complexidade de tempo de melhor caso da classificação de heap.Complexidade média de caso: ocorre quando os elementos na matriz não são organizados em uma ordem ascendente ou descendente adequada, resultando em uma ordem confusa. O(n log n) é a complexidade de tempo médio do heap sort.Pior caso de complexidade: Isso acontece quando você precisa classificar os elementos da matriz na ordem inversa, o que significa que, se os elementos estiverem inicialmente em ordem decrescente ordem, você precisará classificá-los em ordem crescente. O(n log n) é a complexidade de tempo de pior caso da classificação de heap.
Complexidade de espaço
A complexidade de espaço da classificação de heap é O(1)
Como o algoritmo de classificação de heap é implementado?
Veja como a classificação de heap é implementada na linguagem de programação Java.
//Para empilhar uma subárvore. Aqui “i” é o índice do nó raiz em arr[] e “x” é o tamanho do heap
public class HeapSort {
public static void sort(int[] arr) {
int x=arr.length;
//reorganizar array (Build heap)
for (int i=x/2 – 1; i >=0; i–)
heapify(arr, x, i);
//extrai um elemento um a um da pilha
for (int i=x – 1; i > 0; i–) {
//move a raiz inicial para o final
int temp=arr[0];
arr[0]=arr[i];
arr[i]=temp;
//chama a função de máximo heapify no heap reduzido
heapify(arr, i, 0);
}
}
static void heapify(int[] arr, int x, int i) {
int maior=i;//inicializar o maior como raiz
int l=2 * i + 1;//esquerda
int r=2 * i + 2;//direita
//se o filho esquerdo for maior que a raiz
if (l x && arr[l] > arr[maior])
maior=l;
//se o filho certo for maior que o maior até agora
if (r x && arr[r] > arr[maior])
maior=r;
//se o maior não for a raiz
if (maior !=i){
int swap=arr[i];
arr[i]=arr[maior];
arr[maior]=troca;
//empilha repetidamente a subárvore afetada
heapify(arr, x, maior);
}
}
//uma função para imprimir uma matriz de tamanho x
static void printArray(int[]) {
int x=arr.length;
for (int i=0; i x; ++i)
System.out.print(arr[i] + ” “);
System.out.println();
}
//Código do driver
public static void main (String[] args) {
int[] arr={ 13, 12, 14, 6, 7, 8 };
sort(arr);
System.out.println(“Matriz classificada é”);
printArray(arr);
}
}
Saída
Esta é a matriz de números inteiros classificados em ordem crescente.
A matriz classificada é
6, 7, 8, 12, 13, 14
Prós e contras do algoritmo de classificação de heap
Prós
Eficiência: Este algoritmo de classificação é muito eficiente, pois o tempo necessário para classificar um heap aumenta logaritmicamente, enquanto em outros algoritmos o tempo cresce exponencialmente mais lento à medida que os itens de classificação aumentam.Simplicidade: Comparado a outros algoritmos igualmente eficientes, é mais simples, pois não usa princípios avançados de ciência da computação, como recursão.Uso de memória: a classificação de pilha usa memória mínima para manter a lista inicial de itens a serem classificados , e nenhum espaço de memória adicional é necessário para funcionar.
Desvantagens
Caro: a classificação de heap é cara.Instável: a classificação de heap não é confiável, pois pode reorganizar a ordem relevante dos elementos.Ineficiente: Ao lidar com dados altamente complexos, o Heap Sort não é muito eficiente.
Aplicações de Heap Sorting
Você pode ter encontrado o algoritmo de Dijkstra, que usa heap sort para determinar o caminho mais curto. Na estrutura de dados, a classificação de heap permite a recuperação rápida do menor (mais curto) ou maior (mais longo) valor. Ele tem várias aplicações, incluindo determinar a ordem nas estatísticas, gerenciar filas de prioridade no algoritmo de Prim (também conhecido como árvore geradora mínima) e realizar codificação Huffman ou compactação de dados.
Da mesma forma, vários sistemas operacionais usam o Heap algoritmo de ordenação para tarefas e gerenciamento de processos, pois é baseado em uma fila de prioridade.
Em um cenário real, a ordenação por heap pode ser aplicada em uma loja de cartão SIM, onde temos uma longa fila de clientes esperando para ser atendido. Os clientes que precisam pagar suas contas podem ser priorizados, pois seu trabalho leva o mínimo de tempo. Essa abordagem economizará tempo para muitos clientes e evitará atrasos desnecessários, levando a uma experiência mais eficiente e satisfatória para todos.
Resumo
Cada algoritmo de classificação ou pesquisa tem suas vantagens e desvantagens , e a classificação de heap não é exceção. No entanto, as desvantagens do Heap Sort são relativamente mínimas. Por exemplo, não requer nenhum espaço de memória adicional além do que já está alocado.
O tempo é outro fator. Descobriu-se que a complexidade de tempo é determinada usando nlog(n), mas a classificação do heap real é menor que O(nlog(n)). Isso ocorre porque a extração da classificação de heap reduz o tamanho, levando menos tempo à medida que o processo avança. Portanto, Heap Sort é amplamente considerado como um dos “melhores” algoritmos de classificação no domínio da Estrutura de Dados por vários motivos.
O que é Heap Sort e como você pode usá-lo? Perguntas frequentes (perguntas frequentes)
O que significa heapify?
Heapify é o processo de construção de uma estrutura de dados heap a partir de uma representação de matriz de um binário árvore. Este processo pode ser usado para criar um Max-Heap ou um Min-Heap. Ele começa a partir do último índice do nó não-folha na árvore binária, cujo índice é dado por n/2 – 1. O Heapify é implementado usando recursão.
Como funciona o Heap Sort?
Heap sort é um algoritmo de classificação baseado em comparação. Ele funciona movendo os maiores elementos da região não classificada para a região classificada, reduzindo assim a região não classificada. Heap sort visualiza os elementos da matriz como um heap e é conhecido por ter um tempo de execução ideal. Esse algoritmo é útil quando você deseja manter a ordem enquanto extrai o elemento mínimo ou máximo do array.
Como você “empilha” uma árvore?
Para remodelar ou amontoar uma árvore binária, você começa selecionando um nó como o nó raiz da subárvore. Em seguida, você compara o valor do nó raiz com os valores de seus nós filhos esquerdo e direito. Se algum dos nós filhos tiver um valor maior (no caso de um heap máximo) ou menor (no caso de um heap mínimo) do que o nó raiz, você troca os valores do nó raiz e do nó filho por o maior (ou menor) valor. Depois de trocar os valores, você empilha recursivamente a subárvore com raiz no nó filho até que toda a subárvore satisfaça a propriedade de heap. Você repete esse processo para cada nó na árvore até que toda a árvore satisfaça a propriedade heap.
A complexidade de tempo de heapify é O(log n), onde n é o número de nós na subárvore que está sendo heap.
O que é um heap binário?
Um heap binário é uma estrutura de dados que pode ser considerada como uma árvore binária completa onde cada nó pai é menor ou igual a seus filhos (em um heap mínimo) ou maior ou igual a seus filhos (em um heap máximo).
Quais são as vantagens do heap sort?
As vantagens do heap sort incluem sua complexidade de tempo de O(n log n), que é mais rápida do que alguns outros algoritmos de classificação populares, como o bubble sort e o insert sort. Além disso, a classificação por pilha consome pouca memória, pois requer apenas uma quantidade constante de espaço extra.
Quais são as desvantagens da classificação por pilha?
O As desvantagens do heap sort incluem sua propriedade de classificação não estável, o que significa que a ordem relativa de elementos iguais pode não ser preservada após a classificação. Além disso, o heap sort não é muito eficiente para arrays pequenos e sua natureza recursiva pode levar a um desempenho mais lento em algumas arquiteturas.