© Oselote/Shutterstock.com
O algoritmo de classificação de bolhas é um exemplo de um algoritmo de classificação simples. Esse tipo de algoritmo organiza caracteres, strings ou números em uma ordem específica determinada pelo problema que você está resolvendo com seu código.
Uma classificação geralmente é útil quando você deseja organizar os itens em ordem alfabética ou numérica. Os algoritmos de classificação são uma parte crucial da programação, e o tipo de bolha é o favorito entre os alunos devido à sua simplicidade. No entanto, não é a melhor escolha se você precisar de desempenho rápido.
Se Se você quer aprender mais sobre o algoritmo Bubble Sort e como ele funciona, você está no lugar certo. O artigo de hoje detalha como o algoritmo de classificação por bolhas funciona e mostra como implementá-lo. Vamos entrar nisso!
O que é o algoritmo Bubble Sort?
Algoritmos de classificação fornecem uma maneira de apresentar dados logicamente quando você executa seu código. Quando você está aprendendo a programar, o bubble sort é um dos primeiros algoritmos que você aprenderá porque permite que você visualize como um algoritmo de classificação funciona em um nível fundamental.
O algoritmo de classificação de bolhas é único porque só pode comparar dois conjuntos de dados adjacentes. Ele se move por toda a matriz, dicionário, lista ou string e compara cada item e classifica tudo de acordo com suas necessidades.
O algoritmo
Antes de explorarmos como criar um tipo de bolha em seu código, vejamos como funciona passo a passo:
Primeiro, identificaríamos uma coleção de dados que precisa ser classificada. Pode ser uma coleção de números, palavras ou letras que você pretende organizar de uma maneira específica. Uma função comum de um tipo de bolha seria pegar uma lista de números e ordená-los por seu valor, do menor para o maior ou do maior para o menor. O algoritmo começa no primeiro item de uma lista, que seriam os dados no índice 0. Ele compara esses dados com os dados do índice 1 para determinar se uma troca é necessária. Se uma troca for feita, temos um sinalizador que definimos, o que nos permite sair do algoritmo para torná-lo mais eficiente. Em seguida, ele compara índice 1 para o índice 2, e continua na lista até chegar ao fim. Uma vez que o algoritmo passou uma vez, ele precisa passar pelo processo novamente porque não é concluído até que nenhuma mudança precise ser feita. Isso normalmente é feito com loops aninhados que executam uma classificação de bolha em toda a lista até que um condicional, operando no sinalizador, saia depois que passamos por uma iteração completa sem alterações. Depois que esses loops aninhados forem executados, a lista classificada será estar na ordem pretendida para que você possa exibi-lo na tela ou usá-lo para outras operações em seu código.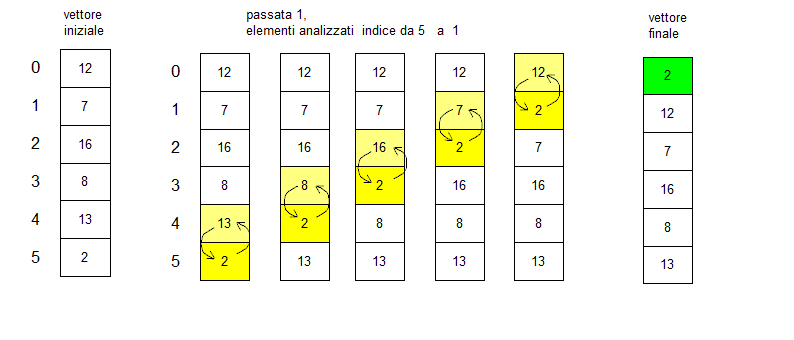 
O algoritmo Bubblesort é ilustrado com um diagrama.
©By Stefano furin – Trabalho próprio, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=37141358
Funcionamento do algoritmo Bubble Sort
Agora que cobrimos a lógica do algoritmo de ordenação de bolhas, vamos nos aprofundar em um exemplo. Vamos pegar uma lista de números que estão fora de ordem e deixar que o balão os organize em ordem crescente.
Para simplificar, usaremos uma lista de quatro números:
29, 15, 0,-5
O primeiro cálculo que o Bubble Sort faria seria verificar os valores do índice 0 e do índice 1 conforme discutimos acima. Como 29 é maior que 15, suas posições irão mudar, dando-nos esta sequência de números:
15, 29, 0,-5
Em seguida, o algoritmo compara 29 e 0. Aqui está a lista resultante:
15, 0, 29,-5
Na última vez nesta primeira iteração, o algoritmo compara 29 a-5, nos dando esta lista:
15, 0,-5, 29
Nossa lista não está exatamente onde precisamos, e a próxima iteração nos ajudará a classificar isso. Veremos a lista mudar desta forma:
0, 15,-5, 29
0,-5, 15, 29
0,-5, 15, 29
0,-5, 15, 29
Então a terceira iteração nos daria este resultado:
-5, 0, 15 , 29
-5, 0, 15, 29
-5, 0, 15, 29
-5, 0, 15, 29
Agora, como a lista está totalmente ordenada, precisaremos de uma maneira de dizer ao loop para parar de executar. Isso é para torná-lo mais eficiente. Para fazer isso, normalmente usamos uma variável booleana junto com algumas declarações condicionais para permitir que o algoritmo saia do loop uma vez que nenhuma troca tenha sido feita.
Implementação do algoritmo Bubble Sort usando um loop For
Agora, vamos lançar algum código para o algoritmo de classificação de bolhas em Python para obter uma boa compreensão de como ele funciona como um método de classificação. Aqui está como poderíamos implementá-lo com um loop for:
def bubbleSort (numArray, z): for a in range(z-1): swap=False for b in range (0, z-a-1): if numArray[b] > numArray[b+1]: swap=True numArray[b], numArray[b+1]=numArray[b+1], numArray[b] se não trocar: retorna numArray numberArray=[82, 67 , 0,-500,-80, 99, 2] x=len(numberArray) print (“Sorted Array:”) print (bubbleSort(numberArray, x))
Explicação do código
Vamos quebrar esse código passo a passo para entendermos o que está acontecendo.
Inicializando o Array
Primeiro, precisamos inicializar nosso array com um conjunto de números que gostaria de classificar (numberArray). Estes são inicializados deliberadamente em ordem aleatória para demonstrar como funciona o algoritmo de ordenação de bolhas. Em seguida, inicializamos uma variável que hospeda a contagem de itens que temos no array (x). Usaremos essa variável posteriormente para controlar quantas vezes iteramos no loop.
Definindo o algoritmo Bubble Sort
Dois valores são passados para o algoritmo, que é definido como bubbleSort. O primeiro valor é o próprio array. Então também passamos o comprimento do array. Dentro do algoritmo, eles são reatribuídos como numArray e z, respectivamente.
O loop que usamos para executar o bubble sort irá iterar um certo número de vezes, mas nem sempre é necessário que ele siga seu curso. Portanto, devemos primeiro configurar uma variável booleana no início do loop for externo que mudará de False para True no loop interno se uma troca for feita durante nosso algoritmo de classificação.
Como falamos sobre anteriormente, um algoritmo de classificação de bolha compara dois valores adjacentes para determinar se a matriz precisa ser alterada. Então, configuramos uma condicional para determinar qual valor é o mais alto. Se o valor da primeira variável for maior, ela trocará de lugar com o item adjacente no array. E, como uma troca foi feita, também definiremos o valor booleano (swap) como True para não sairmos do loop ainda.
Depois que o loop interno tiver passado pelo array na primeira vez, o valor booleano será definido como True, então vamos para o loop externo na segunda vez, definindo o booleano (swap) como False novamente para iniciar todo o processo. Este booleano deve ser reinicializado a cada vez porque queremos que nosso algoritmo seja capaz de sair na primeira vez que passarmos pelo loop interno uma vez sem uma troca. Você pode passar por todo o processo sem uma condição de saída, mas seu programa será executado mais rapidamente com ela implementada.
Visitando os intervalos
O algoritmo de classificação por bolhas continuará esse processo até que Passamos por uma iteração completa do loop interno sem fazer uma troca. Na sintaxe do loop for, o intervalo informa ao loop quando iniciar, parar e quantos passos devem ser incrementados. Ele pode receber três parâmetros, mas precisa apenas de um-em que ponto o loop for deve parar.
Em nosso loop for externo, precisamos apenas dizer onde parar, que é no último índice da matriz. Temos que usar z-1 como o intervalo lá porque o índice começa numerando em 0 em vez de 1. Portanto, se deixássemos em z, ele iria mais uma vez do que precisávamos.
Em nosso for, temos dois parâmetros porque queremos dizer onde começar — no primeiro índice, 0 — e onde parar. Paramos um pouco antes do loop for externo porque não precisamos verificar os itens restantes no array.
Atualizando o array
A instrução if cria uma condição para determinar se os dois itens adjacentes na matriz precisarem trocar de posição. Como estamos classificando os números em ordem crescente, se o primeiro número for maior que o segundo número comparado, esse primeiro número precisa mover uma casa para a direita, o que significa que o segundo número precisa mover uma casa para a esquerda, pois é menor.
Essa troca pode acontecer de algumas maneiras diferentes, mas a maneira mais rápida e fácil de fazer isso é atribuir os valores aos itens adjacentes ao mesmo tempo. Isso é feito com a seguinte instrução: numArray[b], numArray[b+1]=numArray[b+1], numArray[b]. Um método alternativo seria criar uma variável temporária para conter um dos valores que precisam ser movidos enquanto o outro é movido com uma atribuição simples. Mas, como isso requer mais código, é muito mais eficiente realizar quando atribuímos os dois ao mesmo tempo.
Saída de resultados
Quando o método bubbleSort sai do método aninhado for loops e retorna ao programa principal, ele envia o array resultante para a instrução print da qual chamamos o método e exibe os resultados na tela, nos dando um array com sete itens classificados em ordem crescente por valor numérico.
A matriz classificada que receberíamos de nosso exemplo:
[-500,-80, 0, 2, 67, 82, 99]
Melhores e piores casos de uso do Bubble Sort Algoritmo
O algoritmo de classificação por bolhas funciona eficientemente quando temos um número limitado de itens de dados que precisamos organizar em uma determinada ordem. Quando você aumenta ou adiciona muitos pontos de dados, o tipo de bolha começa a ter problemas. Se você precisa de um algoritmo mais eficiente, há muitas opções. Você pode procurar mesclar classificação e classificação rápida, ambas significativamente mais rápidas.
Vamos observar a complexidade de tempo e espaço para ter uma ideia do desempenho.
Complexidade de tempo do algoritmo Bubble Sort
(N representa o número de itens no conjunto de dados.)
O melhor caso existe quando a matriz já está classificada e não precisa fazer nenhuma alteração. No entanto, antes do início do algoritmo de classificação, o programa não sabe disso, portanto, deve seguir as etapas para classificar a matriz pelo menos uma vez.
Isso não é comum ao lidar com dados que você precisa classificar. Muitas vezes, estamos trabalhando com dados inseridos por um usuário ou extraídos de outro método executado pelo programa. E não é a maneira mais eficiente de projetar um programa que exija que o usuário insira dados em ordem alfabética ou numérica.
Complexidade espacial do algoritmo Bubble Sort
O algoritmo de ordenação de bolhas não tem uma grande necessidade de espaço. Porque, no máximo, estamos apenas adicionando um booleano para verificar trocas e variáveis temporárias para manter os dados enquanto trocamos, se necessário. Por esse motivo, a complexidade do espaço não muda quando usamos conjuntos maiores de dados.
Resumo
O algoritmo de classificação por bolhas pode ser eficiente quando você deseja apenas classificar pequenas quantidades de dados. Mas realmente não é o mais eficiente e não é o ideal devido ao seu desempenho. Em vez disso, é mais útil como uma ferramenta de aprendizado para programadores iniciantes aprenderem como o computador executa algoritmos. Se você estiver fazendo um curso de estruturas de dados e algoritmos, terá que dominar este. Depois de compreender os fundamentos dos algoritmos de classificação, você pode evoluir para algoritmos mais eficientes.
O que é o algoritmo de classificação por bolhas e como ele funciona? (com exemplos) FAQs (perguntas frequentes)
O que é o algoritmo de classificação por bolhas?
Um algoritmo de classificação por bolhas é um algoritmo de classificação simples que compara dois valores adjacentes e faz uma troca com base em uma condição configurada em nosso código. Ele normalmente usa um loop while ou um loop for para percorrer cada conjunto de itens adjacentes até atingir o final do conjunto de dados. No entanto, requer mais de uma iteração do conjunto de dados completo para classificar os dados em ordem crescente ou decrescente.
Quais são as limitações do algoritmo de classificação por bolhas?
Quando temos grandes conjuntos de dados, o algoritmo de classificação por bolhas não é o melhor uso do poder de nosso computador. Outros algoritmos de classificação seriam escolhas melhores porque provavelmente não levariam tanto tempo para executar o algoritmo.
Qual é a complexidade de tempo do algoritmo de classificação por bolhas?
A complexidade de tempo varia de 0 (N) a 0 (N^2), onde o melhor cenário existe quando o conjunto de dados já está classificado. N representa o número de itens no conjunto de dados, portanto, a complexidade do tempo pode aumentar muito ao trabalhar com grandes coleções de dados.
Qual é a complexidade do espaço do algoritmo de ordenação de bolhas?
A complexidade do espaço, independentemente do tamanho do nosso conjunto de dados, é O(1), o que significa que permanece a mesma. Em teoria, se você tivesse um conjunto de dados de 200 itens, ocuparia a mesma quantidade de espaço que um com 100.
Quando o algoritmo de ordenação por bolhas deve ser usado?
Por ser mais eficaz com pequenos conjuntos de dados, o algoritmo de classificação por bolhas é mais útil em ambientes educacionais, quando os programadores iniciantes estão aprendendo como codificar algoritmos de classificação.
O que Existem diferentes maneiras de implementar o algoritmo de classificação de bolhas?
Como precisamos iterar todo o conjunto de dados para executar um algoritmo de classificação de bolhas, ele geralmente é implementado com loops-um loop for ou um loop while.
Quais são as alternativas para o algoritmo de classificação por bolhas?
Existem vários algoritmos que podemos usar para executar uma classificação. A seguir estão alguns dos métodos de classificação mais usados: classificação por seleção, classificação por inserção, classificação por balde, classificação por heap e classificação por mesclagem.