© Song_about_summer/Shutterstock.com
Al buscar a través de gráficos o estructuras de datos de árboles, dos algoritmos populares son la búsqueda primero en profundidad (DFS) y la búsqueda primero en amplitud (BFS). Ambos tienen el mismo propósito de encontrar un camino o recorrer un gráfico; sin embargo, DFS vs. BFS difieren en cuanto a su enfoque y eficiencia.
DFS es recursivo, atraviesa profundamente el gráfico y retrocede cuando llega a callejones sin salida, mientras que BFS visita iterativamente todos los nodos adyacentes antes de avanzar. Este artículo contrastará DFS y BFS describiendo las diferencias clave, así como los pros y los contras asociados con cada enfoque.
DFS vs. BFS: Comparación lado a lado
DFS vs. BFS: ¿Cuál es la diferencia?
A primera vista, Breadth-First Search (BFS) y Depth-First Search ( DFS) los algoritmos parecen similares. BFS atraviesa según la anchura del árbol, mientras que DFS sigue la profundidad. Ambos comparten un objetivo común: buscar a través de gráficos para localizar un nodo o ruta individual. Por lo tanto, las diferencias clave entre ellos se analizarán más adelante.
Aproximación y orden transversal
DFS (búsqueda primero en profundidad) y BFS (búsqueda primero en amplitud) son dos algoritmos ampliamente utilizados. para atravesar gráficos y árboles. Ambos algoritmos visitan cada nodo o vértice del gráfico o árbol; sin embargo, su orden de recorrido y enfoque varía.
DFS adopta un enfoque de profundidad primero, atravesando cada rama por turno hasta que alcanza la profundidad de cada uno. En otras palabras, explora lo más posible a lo largo de cada rama antes de retroceder. El orden transversal utilizado por DFS es LIFO (Último en entrar, primero en salir), lo que significa que utiliza una estructura de datos de pila para almacenar los nodos visitados.
Por el contrario, BFS adopta un enfoque de amplitud primero; visita todos los nodos a la profundidad actual antes de pasar a los que se encuentran a mayor profundidad. Es decir, analiza cada nodo en cada nivel antes de avanzar hacia abajo. Además, su orden transversal es FIFO (First In First Out), que utiliza una estructura de datos de cola para almacenar los nodos visitados.
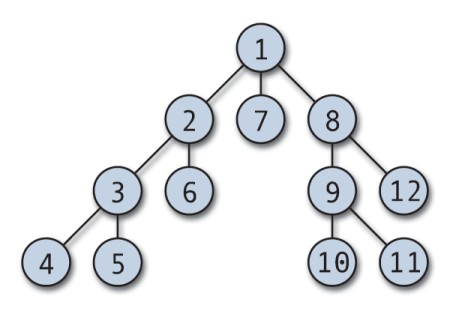El algoritmo DFS buscará lo más abajo posible en cada rama antes de retroceder.
©Wolfram Esser/CC BY-SA 3.0 – Licencia
Complejidad de tiempo y espacio
Otra diferencia significativa entre DFS y BFS es su complejidad de tiempo y espacio. La complejidad temporal de DFS es O(V+E), donde V es el número de vértices y E es el número de aristas en un gráfico o árbol. Además, su complejidad espacial también supera a O(V+E) ya que todos los nodos visitados deben almacenarse en una pila hasta llegar a sus respectivas hojas.
Por el contrario, BFS tiene una complejidad temporal de O(V+E) , similar a DFS; sin embargo, su complejidad espacial es O(V), ya que almacena todos los nodos visitados en una matriz. Por lo tanto, BFS puede requerir más memoria que DFS cuando se trata de gráficos o árboles grandes.
Casos de uso y aplicaciones
DFS y BFS tienen usos y aplicaciones distintos. DFS se emplea a menudo cuando el espacio de búsqueda es grande y profundo, con el objetivo de explorar cualquier camino dado antes de retroceder. También puede ser beneficioso cuando se trata de encontrar una solución en juegos o acertijos donde la respuesta puede estar ubicada en lo más profundo del espacio del acertijo.
BFS, por otro lado, se emplea a menudo cuando se busca en un espacio grande y espacio de búsqueda poco profundo para identificar el camino más corto entre dos nodos o vértices. También determina la distancia más cercana entre dos nodos de red o ubicaciones en un mapa geográfico.
Integridad y optimización
Los algoritmos de búsqueda deben cumplir dos requisitos esenciales: integridad y optimización. La completitud se refiere a si el algoritmo puede garantizar la búsqueda de una solución, si existe, mientras que la optimización implica encontrar el camino más corto u óptimo hacia esa solución.
DFS no es perfecto ni óptimo, ya que puede atascarse en un bucle infinito o fallar en encontrar el camino más corto. DFS podría atascarse si un ciclo en su gráfico o árbol no logra rastrear los nodos visitados. Además, DFS puede encontrar rutas subóptimas para resolver problemas.
Sin embargo, BFS es completo y óptimo. Garantiza encontrar una solución si existe, así como encontrar el camino más corto en ella. Después de explorar todos los nodos en un nivel de profundidad antes de pasar a otro, BFS se asegura de encontrar el camino más corto. No obstante, BFS puede tardar más que DFS en algunos casos, especialmente cuando se trata de gráficos o árboles profundos o angostos.
Gestión de la memoria
Otro factor crucial al seleccionar entre DFS y BFS es la memoria. gestión. La administración de memoria se refiere a cómo un algoritmo usa la memoria y cuánto espacio es necesario para almacenar los nodos visitados.
DFS usa una pila para almacenar los nodos visitados, pero los espacios de búsqueda o los gráficos grandes pueden causar problemas. En tales casos, DFS puede quedarse sin memoria y no encontrar una solución óptima; los gráficos o árboles densos requieren más memoria debido a los ciclos frecuentes.
BFS se basa en una estructura de datos de cola para almacenar los nodos visitados, lo que garantiza que no se quede sin memoria. Sin embargo, en ciertas circunstancias, BFS puede usar más memoria que DFS, especialmente cuando el gráfico o árbol es ancho y poco profundo o tiene muchas ramas. BFS también podría requerir más recursos si hay muchos nodos o la estructura es escasa.
Complejidad de implementación
La complejidad de implementación de un algoritmo se refiere a qué tan fácil o difícil es ejecutarlo. Esto depende del lenguaje de programación utilizado, las estructuras de datos disponibles y cualquier lógica necesaria para una finalización exitosa.
DFS suele ser más fácil de implementar que BFS, ya que solo necesita una estructura de datos de pila y una función o bucle recursivo. DFS se puede implementar utilizando un sencillo algoritmo de búsqueda en profundidad que visita cada nodo antes de explorar cada rama por turno. Además, es más sencillo de implementar en lenguajes de programación recursivos como Python, donde la recursión es algo natural.
BFS, en por otro lado, requiere una estructura de datos de cola y un bucle. Para implementarlo de manera eficiente, BFS utiliza un algoritmo de búsqueda primero en amplitud que visita todos los nodos en una profundidad antes de pasar al siguiente. Sin embargo, implementar BFS en lenguajes de programación recursivos como Python puede ser más desafiante ya que requieren un bucle real en lugar de una simple recursividad.
Aplicaciones
DFS y BFS tienen aplicaciones distintas en varios dominios. DFS se emplea comúnmente en gráficos por computadora, inteligencia artificial y rastreo web para ofrecer modelos e imágenes 3D mediante la exploración del espacio 3D para representar objetos. La inteligencia artificial usa DFS para árboles de decisión o árboles de juegos, evaluando cada movimiento posible para explorar las ramas del árbol, mientras que los rastreadores web usan DFS para rastrear la web y explorar enlaces en las páginas.
BFS ha sido ampliamente utilizado en la red enrutamiento, algoritmos de ruta más corta y rompecabezas. En el enrutamiento de redes, encuentra el camino más corto entre dos nodos explorando todos los caminos potenciales hasta encontrar el más corto. BFS también juega un papel en los algoritmos de ruta más corta como el de Dijkstra o A* que garantiza encontrar la ruta más corta; De manera similar, al resolver acertijos como el Cubo de Rubik usando BFS, puedes determinar la solución más corta que resuelve el acertijo.
Usar BFS para resolver el cubo de Rubik determinará la solución más rápida para resolver el rompecabezas.
©gd_project/Shutterstock.com
Espacio de búsqueda
El espacio de búsqueda es el conjunto de todos los estados o configuraciones posibles que un algoritmo puede explorar para encontrar su solución. Se puede representar como un gráfico o árbol, donde cada nodo representa un estado o configuración, y cada borde significa una transición entre ellos.
DFS investiga el espacio de búsqueda de manera profunda, explorando cada rama en la medida de lo posible. como sea posible antes de retroceder y explorar otras ramas. Este enfoque funciona mejor para espacios de búsqueda grandes y profundos en los que la solución puede estar en lo más profundo. Desafortunadamente, DFS puede atascarse en un bucle infinito si hay un bucle infinito presente y no realiza un seguimiento de los nodos visitados.
BFS atraviesa el espacio de búsqueda de manera amplia, explorando todos los nodos a la vez. profundidad antes de pasar a la siguiente. Es ideal para espacios de búsqueda grandes o poco profundos donde la solución puede estar cerca de la raíz. BFS garantiza encontrar la ruta más corta a esa solución, pero puede requerir más memoria y ser más lento en algunos casos que DFS.
Estrategia de búsqueda
Una estrategia de búsqueda se refiere a un algoritmo que decide qué nodo para explorar a continuación. Factores como el costo, la heurística o la aleatoriedad pueden guiar este proceso de toma de decisiones.
DFS emplea una estrategia de búsqueda en profundidad, en la que explora cada rama en la mayor medida posible antes de regresar y explorar otras ramas. DFS no utiliza ningún costo o heurística al seleccionar qué nodo explorar a continuación; por lo tanto, puede explorar caminos subóptimos. En ciertos casos, DFS también puede depender de la aleatoriedad, como la búsqueda de árbol de Monte Carlo.
BFS generalmente usa una estrategia de búsqueda en amplitud, explorando todos los nodos en una profundidad antes de continuar con el siguiente. Por el contrario, emplea una estrategia de búsqueda de costos uniforme que prioriza los nodos con el costo más bajo. En ciertos casos, BFS también puede depender de heurísticas como el algoritmo A*, que utiliza el costo y la distancia estimada para decidir qué nodo explorar a continuación.
DFS vs. BFS: 10 datos que debe conocer
DFS significa Búsqueda en primer lugar en profundidad, mientras que BFS significa Búsqueda en primer lugar en amplitud. DFS atraviesa un gráfico o árbol en un movimiento hacia la profundidad, mientras que BFS se mueve de acuerdo con la amplitud del árbol. Para realizar un seguimiento de los nodos visitados durante el recorrido DFS, utilizan una pila, mientras que con BFS, utiliza una cola. DFS se puede emplear para la clasificación topológica, la detección de ciclos y la búsqueda de componentes fuertemente conectados en gráficos; mientras que BFS tiene como objetivo encontrar la ruta más corta entre dos nodos. DFS ocupa menos espacio, mientras que BFS requiere más, ya que almacena todos los nodos en el nivel actual antes de pasar al siguiente. DFS es más rápido cuando resuelve problemas que involucran una gran cantidad de nodos. mientras que BFS sobresale cuando se trata de grupos más pequeños. DFS atraviesa todos los nodos en un gráfico o árbol, mientras que BFS solo visita aquellos a lo largo del camino más corto. DFS usa una estrategia de búsqueda en profundidad, mientras que BFS emplea un enfoque en amplitud. encuentre la ruta más corta, mientras que BFS siempre lo hace. Además, DFS podría quedarse atascado en un ciclo infinito si su gráfico contiene ciclos; sin embargo, BFS siempre termina cuando solo quedan nodos finitos.
DFS frente a BFS: ¿Cuál es mejor?
Los algoritmos de búsqueda primero en profundidad (DFS) y búsqueda primero en amplitud (BFS) poseen cada uno sus propias ventajas y desventajas específicas, lo que los hace más adecuados para ciertos escenarios que otros.
DFS atraviesa eficientemente gráficos profundos o infinitos con baja complejidad de espacio e implementación basada en recursividad. También detecta efectivamente los ciclos en un gráfico, ya que explora cada rama antes de retroceder. DFS proporciona soluciones a problemas como encontrar componentes conectados, clasificación topológica y el rompecabezas de 8; las modificaciones son posibles.
Por el contrario, BFS es más adecuado para encontrar la ruta más corta entre dos nodos en un gráfico, ya que examina todos los nodos a esa profundidad antes de pasar al siguiente nivel. Además, se puede emplear para calcular el árbol de expansión mínimo de un gráfico y resolver problemas como Knight’s Tour.
Ambos algoritmos tienen sus propias complejidades de tiempo, y la elección entre ellos depende del problema particular y características del gráfico que se analiza. En términos generales, BFS tiene una mayor complejidad de tiempo que DFS pero garantiza la ruta más corta entre dos nodos en un gráfico no ponderado; por otro lado, DFS puede tener menor complejidad, pero no siempre puede garantizar este camino más corto.
En conclusión, la elección entre DFS y BFS depende del problema que se resuelva y del gráfico que se analice. Ambos algoritmos tienen sus puntos fuertes y débiles; por lo tanto, comprender ambos puede ayudar a seleccionar el más adecuado para un problema específico. Por lo tanto, es esencial tener ambos tipos de algoritmos en su caja de herramientas, junto con ejemplos en los que son más beneficiosos.
DFS vs. BFS: Comparación completa y 9 diferencias clave Preguntas frecuentes (Preguntas frecuentes)
¿Qué algoritmo es mejor para encontrar una ruta entre dos nodos?
BFS y DFS se pueden emplear para encontrar una ruta entre dos nodos. BFS es mejor para encontrar la ruta más corta, mientras que DFS prefiere encontrar rutas que pueden no ser las más cortas pero que pueden tener otras características deseables, como ser de tipo topológico o componente fuertemente conectado.
¿Qué algoritmo es ¿Es mejor para recorrer un gráfico disperso?
BFS es superior para recorrer un gráfico disperso, ya que explora todos los nodos en un nivel antes de continuar, lo que lo hace eficiente cuando hay pocos bordes. Por el contrario, DFS puede explorar muchos nodos no relacionados, lo que lo hace menos eficiente cuando se trabaja en gráficos dispersos.
¿Qué algoritmo es mejor para recorrer un gráfico denso?
DFS es más eficiente al atravesar un gráfico denso, ya que explora los nodos en profundidad y puede retroceder rápidamente a aquellos que aún son relevantes para la búsqueda. Sin embargo, BFS puede sondear muchos nodos irrelevantes a la vez antes de llegar al nodo deseado, lo que lo hace menos efectivo en redes densas.
¿Se pueden usar DFS y BFS para encontrar los componentes conectados de un gráfico?
Sí, tanto DFS como BFS se pueden emplear para descubrir los componentes conectados de un gráfico. DFS comienza desde un nodo y atraviesa lo más lejos posible antes de regresar y explorar otros nodos no visitados, mientras que BFS examina todos los nodos en un nivel antes de avanzar al siguiente.
¿Se pueden usar DFS y BFS para detectar ciclos en un gráfico?
Sí, tanto DFS como BFS se pueden usar para detectar ciclos en gráficos. DFS detecta ciclos al realizar un seguimiento de los nodos visitados en una lista y una pila de nodos que se están explorando; si ese mismo nodo reaparece sin ser su padre en ningún orden, entonces se considera un nuevo ciclo. De manera similar, BFS mantiene listas de nodos visitados y una cola activa de nodos que se están explorando; si un nodo visitado anteriormente reaparece sin ser su propio hijo dentro de esta última cola, se marca como potencialmente dañino.
¿Se pueden usar DFS y BFS para encontrar el tipo topológico de un gráfico acíclico dirigido ( DAG)?
Sí, tanto DFS como BFS se pueden emplear para determinar el tipo topológico de un DAG. Con DFS, esto se hace manteniendo un índice de los nodos visitados, así como una pila continua de los que se están explorando. Una vez que se han explorado todos los hijos de cada nodo, se agregan al ordenamiento topológico; De manera similar, en BFS, también hay un índice que realiza un seguimiento de los nodos visitados junto con una cola en curso que espera la exploración; cuando se han explorado todos los padres de un nodo, también se incluye en la ordenación topológica.
¿Se pueden usar DFS y BFS para encontrar la ruta más corta en un gráfico ponderado?
BFS se puede emplear para encontrar la ruta más corta en un gráfico no ponderado, mientras que el algoritmo de Dijkstra se emplea para gráficos ponderados. Sin embargo, DFS también puede tener éxito cuando los pesos no son negativos y la búsqueda se limita a un componente conectado.