© pinkeyes/Shutterstock.com
El algoritmo de Dijkstra es solo un ejemplo de lo que llamamos algoritmo de ruta más corta. En pocas palabras, estos son algoritmos que se utilizan para encontrar la distancia (o camino) más corta entre los vértices de un gráfico.
Si bien la ruta más corta se puede definir de varias formas, como tiempo, costo o distancia, generalmente se refiere a la distancia entre nodos. Si quieres saber más sobre cómo funciona el algoritmo de Dijkstra y para qué puedes usarlo, estás en el lugar correcto.

¿Qué es el algoritmo de Dijkstra?
En términos simples, el algoritmo de Dijkstra es un método para encontrar el camino más corto entre nodos en un gráfico. Se designa un nodo de origen y luego se calcula la distancia entre este nodo y todos los demás nodos utilizando el algoritmo.
A diferencia de otros algoritmos de ruta más corta, el de Dijkstra solo puede funcionar con gráficos ponderados no negativos. Es decir, gráficos donde el valor de cada nodo representa alguna cantidad, como el costo o la distancia, y todos los valores son positivos.
El algoritmo
Antes de sumergirnos en cómo implementar el algoritmo de Dijkstra usando código, repasemos los pasos involucrados:
Primero, inicializamos una cola de prioridad vacía; llamemos a esto”Q”. Esta es la forma más eficiente de usar el algoritmo, ya que garantiza que siempre seleccionemos el siguiente vértice más cercano al nodo de origen. Dado que aún no conocemos las distancias de cada vértice al nodo de origen, inicializamos todas las distancias de los vértices hasta el infinito. La distancia del vértice de origen, o nodo de origen, también se establece en 0, ya que este es nuestro punto de partida. Luego, el nodo de origen se agrega a la cola de prioridad con una prioridad de 0. Para comenzar, el vértice con el valor más pequeño distancia se elimina de la cola. Este vértice se llama”u”y los vértices vecinos se designan como”v”. Se calcula la distancia desde el nodo de origen a cada v a u, y si la distancia es menor que la distancia actual a v, la distancia se actualiza. Una vez que se calcula v, se inserta en la cola de prioridad con su prioridad establecida en equivalente a su distancia desde el vértice fuente. Esto asegura que los vértices con distancias más pequeñas se prioricen primero, manteniendo la eficiencia del algoritmo al considerar primero los vértices no visitados más cercanos.
Funcionamiento del algoritmo de Dijkstra
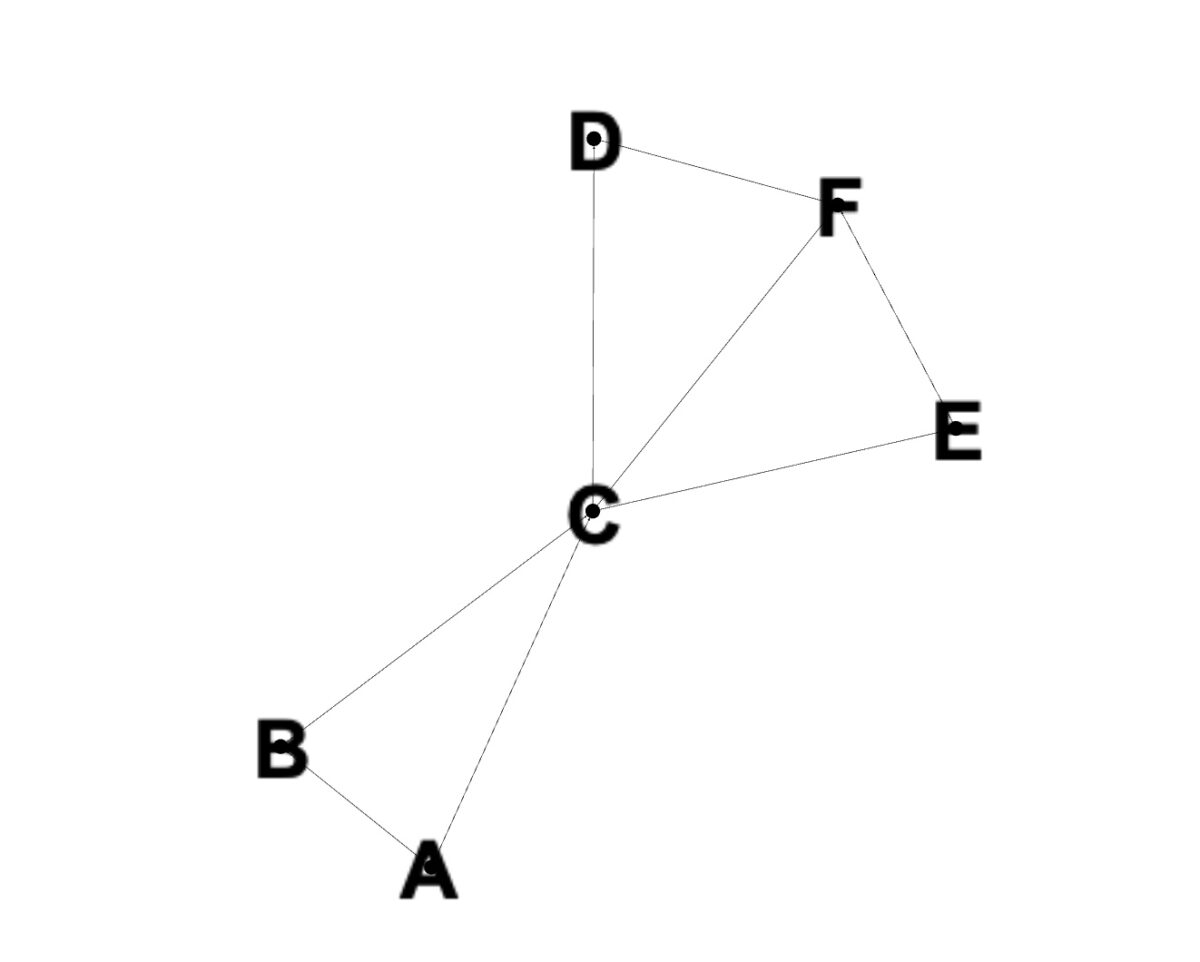 Vértices A a F.
Vértices A a F.
©”TNGD”.com
Ahora que hemos cubierto los conceptos básicos detrás del algoritmo de Dijkstra, echemos un vistazo a cómo funcionaría con un ejemplo. Primero, tome un gráfico con nodos dispuestos de la siguiente manera:
Tenemos vértices A a F, que están conectados entre sí a través de varios caminos. Estas conexiones también se conocen como bordes. Si elegimos A como nuestro vértice inicial, todos los valores de ruta para los otros nodos se establecen en infinito, como se discutió anteriormente.
Luego vamos a cada vértice y actualizamos su longitud de ruta. Si la distancia calculada al nodo adyacente es menor que la distancia actual a este vértice, la distancia se actualiza.
Si establecemos la prioridad de cada vértice igual a su distancia desde la fuente, evitamos visitar los nodos dos veces. Al visitar un nodo no visitado, buscamos primero la longitud de ruta más corta. Este proceso se repite hasta que se ha visitado cada nodo y se calcula la distancia desde el nodo de origen.
Implementación del algoritmo de Dijkstra usando un montón
Es hora de implementar algo de código para el algoritmo de Dijkstra en Python y ver cómo funciona esto. Comenzaremos usando una implementación simple de una cola de prioridad, conocida como montón. El código se puede representar de la siguiente manera:
import heapq import sys def dijkstra_heap(adj_matrix, fuente): num_vertices=len(adj_matrix) distancias=[sys.maxsize] * num_vertices distancias[fuente]=0 visitadas=[Falso] * num_vertices heap=[(0, source)] while heap: current_distance, current_vertex=heapq.heapppop(heap) visitó[current_vertex]=True para vecino_vértice en rango(num_vértices): peso=adj_matrix[actual_vértice][vecino_vértice] si no se visitó [vértice_vecino] y peso !=0: distancia=distancia_actual + peso si distancia distancias[vértice_vecino]: distancias[vértice_vecino]=distancia heapq.heappush(montón, (distancia, vértice_vecino)) return distancias adj_matrix=[ [0, 2, 2 , 0, 0, 0], [2, 0, 2, 0, 0, 0], [2, 2, 0, 2, 2, 6], [0, 0, 2, 0, 2, 2], [0, 0, 2, 2, 0, 2], [0, 0, 6, 2, 2, 0] ] distancias=dijkstra_heap(adj_matrix, 0) print(di posturas)
Explicación del código
Vamos a desglosar este código paso a paso para que podamos entender lo que está pasando.
Importación de módulos
En primer lugar, estamos importando los módulos”heapq”y”sys”. El primer módulo nos permite usar la estructura de datos del montón, mientras que el segundo nos permite usar el valor entero máximo. Esto es necesario porque estamos inicializando las distancias de los vértices hasta el infinito.
Definiendo el algoritmo de Dijkstra
A continuación, definimos”dijkstra_heap”como una función con dos argumentos:”adj_matrix”y”fuente”. Estos son una representación del grafo como una matriz de adyacencia y el índice del nodo fuente, respectivamente.
Visitando los nodos
En este bloque, estamos calculando el número de vértices. Luego, estamos inicializando las distancias desde el vértice de origen hasta cada vértice de destino hasta el infinito, como se mencionó anteriormente. La distancia del nodo de origen también se establece en cero.
Luego se crea una lista, llamada”visitado”, que se inicializa en”Falso”. Esto significa que los nodos inicialmente se consideran no visitados hasta que hayamos calculado la distancia entre ellos y la fuente. También se crea una cola de prioridad, denominada”montón”, con el vértice inicial y la distancia desde el nodo de origen designados como una tupla.
Actualización de las longitudes de ruta más cortas
A continuación, tener un bucle”while”que se ejecuta hasta que la cola está vacía. La primera línea toma el vértice del montón que tiene la distancia más corta desde el vértice de origen, y la segunda línea marca el vértice como visitado una vez que se calcula esta distancia.
Seguimos esto con un bucle”for”. , que itera sobre todos los vecinos del vértice que nos preocupa actualmente. Se recupera el peso de cada borde y se comprueba si se han visitado los nodos vecinos y si los pesos son distintos de cero. Luego, la distancia al nodo vecino se calcula usando la distancia desde la fuente hasta el nodo actual.
Tenemos otra declaración”si”, que verifica si la distancia calculada es más corta que la distancia más corta actual en nuestro lista de”distancias”. Si es así, la siguiente línea actualiza este valor. Finalmente, el vértice vecino, así como su distancia desde el origen, se agregan al montón.
Resultados
Después de que finaliza este proceso, las distancias desde el nodo de origen hasta todos los demás nodos del gráfico regresan a la consola.
El penúltimo bloque de código simplemente representa el gráfico que estamos viendo como una matriz de adyacencia, donde el valor en la celda {i, j} representa el peso del borde que conecta los dos vértices.
El código final simplemente le dice al sistema que calcule las distancias de ruta más cortas y luego las imprima en la consola.
Implementación del código
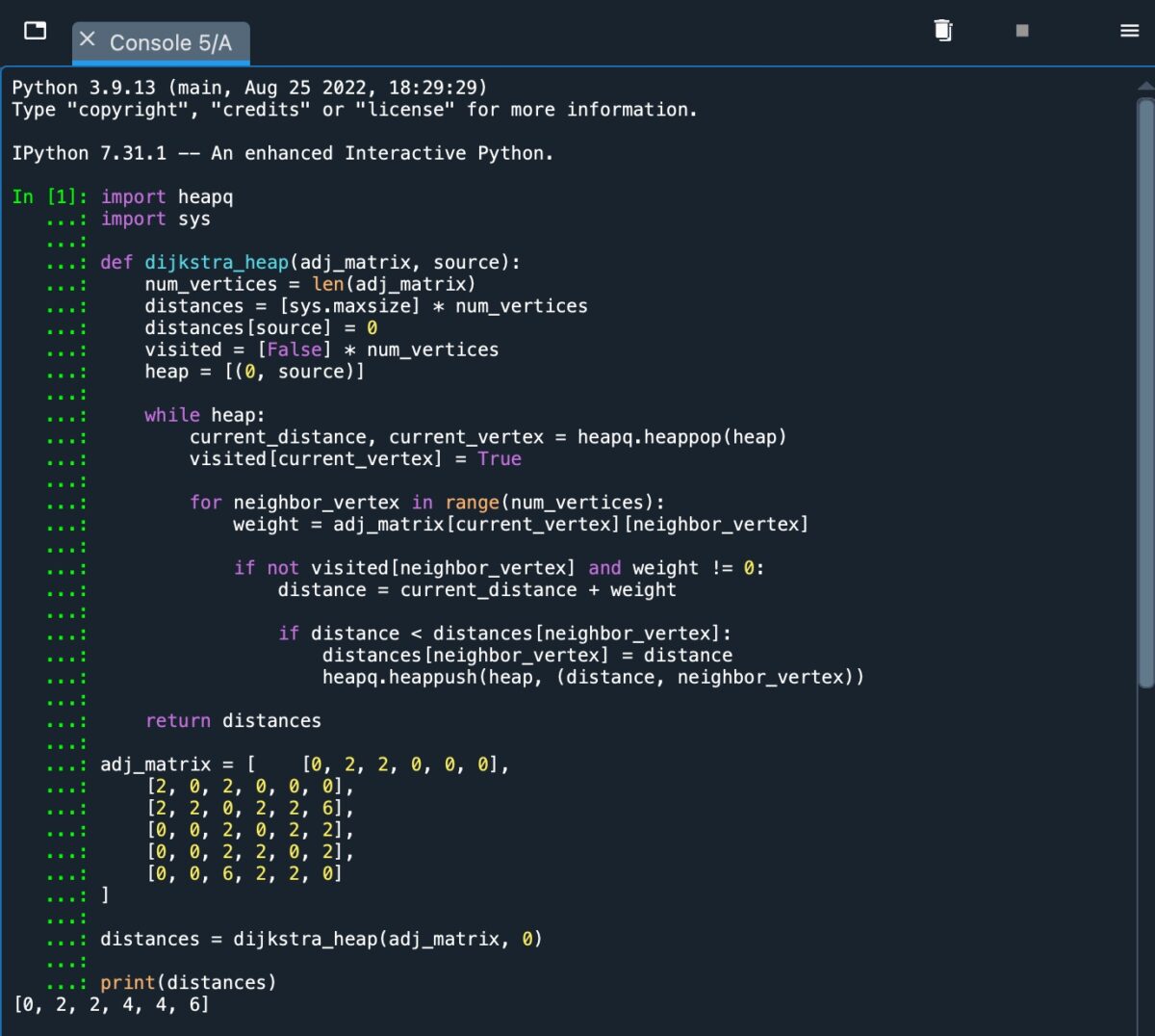 La implementación simple de un heap.
La implementación simple de un heap.
©”TNGD”.com
Como podemos ver en la captura de pantalla, recibimos una salida de [0, 2, 2, 4, 4, 6], que representa la distancia de ruta más corta desde el nodo de origen A hasta los nodos B, C, D, E y F.
Mejor y peor uso Casos del algoritmo de Dijkstra
En términos generales, el algoritmo de Dijkstra se considera eficiente, aunque algunos algoritmos pueden funcionar mejor en casos especializados. Dicho esto, veamos la complejidad de tiempo y espacio del algoritmo de Dijkstra en el mejor, promedio y peor de los casos.
Complejidad de tiempo del algoritmo de Dijkstra
Por lo general, sólo tenemos una complejidad para cada caso. Pero, con el algoritmo de Dijkstra, la situación no es tan clara. Esto se debe a que puede implementar el algoritmo de diferentes maneras, principalmente mediante el uso de una cola de prioridad.
Al usar una cola de prioridad, puede usar un método de almacenamiento dinámico binario o un método de almacenamiento dinámico de Fibonacci. En general, el montón de Fibonacci conduce a un rendimiento más eficiente y a una mejor complejidad temporal en el peor de los casos de O((E + V) log V), donde E es el número de aristas y V es el número de vértices.
Si no está utilizando una cola de prioridad y el gráfico es denso, la complejidad del peor de los casos podría ser tan ineficiente como O (V2 log V).
Con respecto al caso promedio , la complejidad del tiempo es un poco más favorable. El caso promedio se refiere a cuando se usa una cola de prioridad para calcular las distancias mínimas a cada vértice.
El mejor caso, en términos estrictos, es uno inusual. Probablemente no te molestarías en usar el algoritmo para resolverlo. Esto se debe a que, en el mejor de los casos, el vértice de origen es el mismo que el de destino. Esto significa que la iteración finaliza después de solo un ciclo.
La complejidad es, de hecho, idéntica a la del caso promedio. Pero como los valores de E y V son iguales a 1, esto se simplifica a O(1). Si está utilizando un montón para implementar su algoritmo, entonces la complejidad del mejor de los casos cambia a O (E * log V). Esto se debe a que habrá un máximo de vértices O(E) en su cola.
Complejidad espacial del algoritmo de Dijkstra
Al igual que con la complejidad del tiempo, la complejidad del espacio del algoritmo depende de su implementación. Si usa una lista de adyacencia para representar su gráfico y un montón de Fibonacci o un montón normal, la complejidad es igual a O(V+E). Esto se debe a que la distancia del vértice desde el origen, así como los bordes entre los vértices, deben almacenarse en la memoria.
Sin embargo, si usa una matriz de adyacencia, la complejidad se reduce a O( V2). Esto se debe a que necesita almacenar las distancias de los vértices, así como una matriz V * V para representar los bordes.
Conclusión
Para resumir, el algoritmo de Dijkstra es uno de los muchos algoritmos utilizados para calcular las longitudes de ruta más cortas en un gráfico y es muy útil. Si bien hay muchas formas de implementar el algoritmo, usar una cola de prioridad de alguna descripción suele ser la mejor opción.
De estos métodos, usar un montón de Fibonacci tiende a ser el más eficiente, particularmente para gráficos grandes. Sin embargo, para gráficos más pequeños, una cola de prioridad más simple puede ser más que suficiente.
A continuación
Explicación del algoritmo de ruta más corta de Dijkstra, con ejemplos Preguntas frecuentes
¿Qué es el algoritmo de Dijkstra?
El algoritmo se utiliza para calcular las longitudes de ruta más cortas entre los nodos de un gráfico. Es un método iterativo que comienza con la distancia más corta desde el nodo de origen, luego actualiza la distancia a los nodos vecinos a medida que avanza.
¿Cuáles son las limitaciones del algoritmo de Dijkstra?
El algoritmo no puede manejar bordes de peso negativos, lo que dará como resultado resultados incorrectos.
¿Cuál es la complejidad temporal del algoritmo de Dijkstra?
La complejidad del tiempo depende de si está utilizando una cola de prioridad y de cómo la está implementando. En el mejor de los casos, donde solo se necesita una iteración, la complejidad es O(1).
De lo contrario, el mejor de los casos es O(E* log V) u O(E + V log V) , dependiendo de si está utilizando un montón estándar o un montón de Fibonacci.
En cualquier caso, las complejidades para el promedio y el peor de los casos son las mismas. El peor de los casos puede ser equivalente a O(V2 log V) si no está utilizando una cola de prioridad en absoluto.
¿Cuál es la complejidad espacial del algoritmo de Dijkstra?
Depende de la implementación, pero puede ser desde O(V2) hasta O(V + E).
¿Puedes usar el algoritmo de Dijkstra en un gráfico que tiene ciclos?
Sí, siempre que ninguno de los bordes de peso sea negativo.
¿Cuáles son las diferentes formas de implementar el algoritmo de Dijkstra?
Puede usar una cola de prioridad, como un montón o un montón de Fibonacci. Generalmente, un montón de Fibonacci conduce a resultados más eficientes con gráficos más grandes.
¿Cuáles son las alternativas al algoritmo de Dijkstra?
Otros algoritmos de ruta más corta incluyen el A * algoritmo, algoritmo Bellman-Ford y algoritmo Floyd-Warshall. A* tiende a ser más rápido pero requiere más memoria.
Bellman-Ford y Floyd-Warshall pueden manejar bordes de peso negativo a diferencia de Dijkstra, pero ambos son más ineficientes que Dijkstra: tienen complejidades de tiempo de O(VE ) y O(V3) respectivamente.