© TippaPatt/Shutterstock.com
Los informáticos suelen utilizar gráficos para representar datos. Los gráficos pueden representar varias relaciones, desde mapas y compuestos químicos hasta relaciones sociales y redes informáticas. Podemos usar muchos algoritmos con gráficos, como el algoritmo de Dijkstra, la Depth-First Search (DFS) y el algoritmo Breadth-First Search (o BFS). Si bien puede usar ambos algoritmos para recorrer los nodos de un gráfico, BFS es mejor para gráficos no ponderados. En este artículo, vamos a explorar cómo funciona BFS y sus aplicaciones.
¿Qué es BFS?
BFS es un algoritmo de búsqueda. El algoritmo comienza su recorrido en el nodo de origen y luego visita los nodos vecinos. Después de esto, el algoritmo elige el nodo más cercano en el siguiente nivel de profundidad y luego visita los nodos no explorados al lado de este, y así sucesivamente. Dado que el algoritmo BFS visita los nodos en cada nivel antes de pasar al siguiente nivel, de ahí proviene el nombre”Breadth-first”. Nos aseguramos de que solo visitamos cada nodo una vez mediante el seguimiento de los nodos visitados y no visitados. Puede usar BFS para calcular distancias de ruta, al igual que con el algoritmo de Dijkstra.
El algoritmo detrás de BFS
Podemos representar el algoritmo básico con el siguiente pseudocódigo:
BFS(graph, start): cola=[inicio] visitado=establecer (inicio) mientras la cola no está vacía: nodo=dequeue (cola) proceso (nodo) para el vecino en el gráfico. vecinos (nodo): si el vecino no está visitado: visitado. agregar (vecino) enqueue(cola, vecino)
En este caso, estamos definiendo un gráfico como”gráfico”y”inicio”es el nodo de inicio.
Implementamos una estructura de cola para contener los nodos no visitados , así como un conjunto”visitado”para contener los nodos visitados.
El bucle”while”continúa hasta que la cola está vacía e inicia el procesamiento de los nodos nivel por nivel. La función”eliminar la cola”elimina el primer nodo de la cola a medida que se visita.
La función”procesar”realiza alguna función deseada en el nodo, como actualizar la distancia a sus vecinos o imprimir datos para la consola.
El ciclo”for”itera sobre todos los vecinos del nodo actual, verificando si el nodo ya ha sido visitado. Si no, se agrega a la cola usando la función”poner en cola”. En esencia, los nodos en cada nivel se almacenan en la cola, con sus vecinos agregados para ser visitados en el siguiente nivel de profundidad. Esto nos permite determinar la ruta más corta entre el nodo de origen y todos los demás nodos del gráfico.
Funcionamiento de BFS
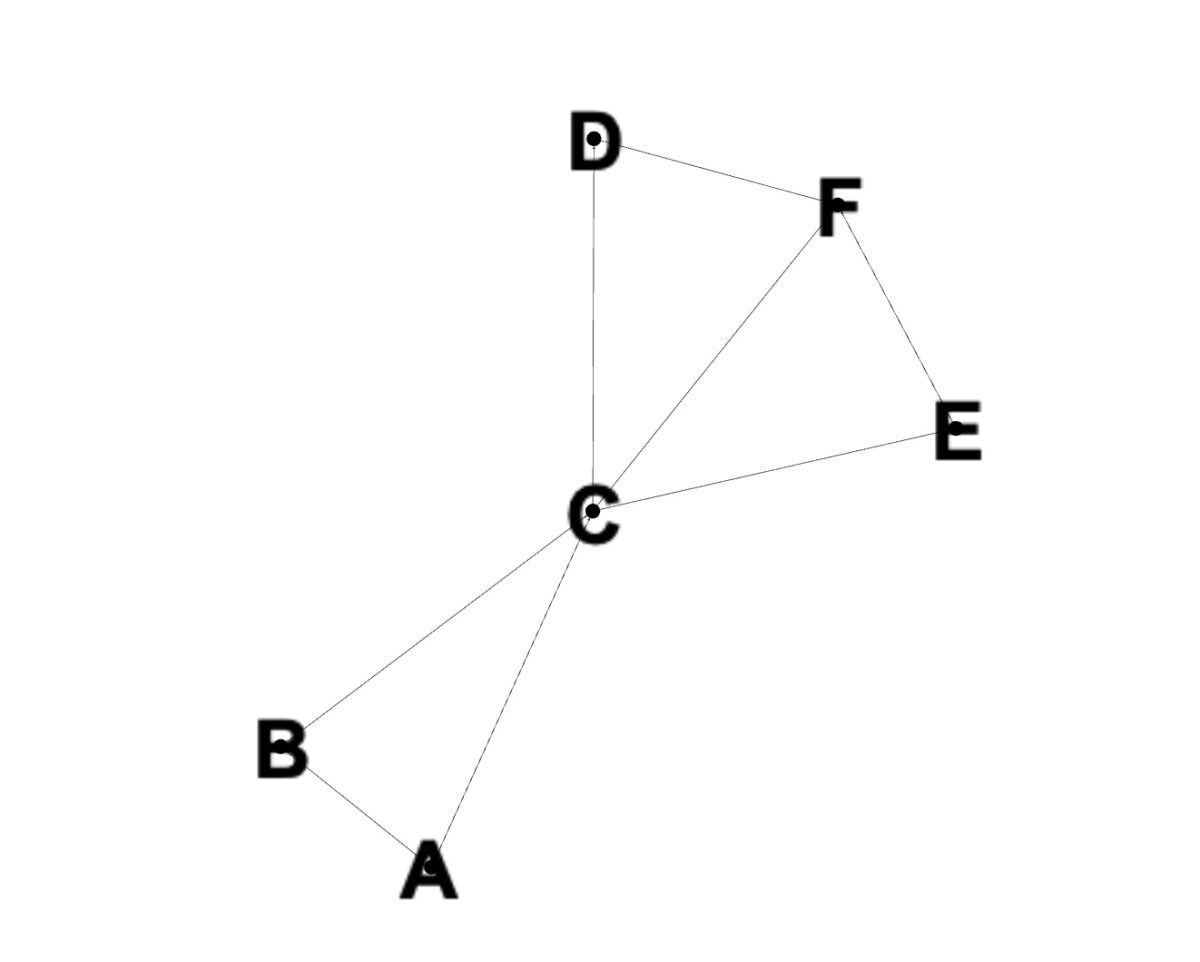Usaremos este gráfico para los siguientes ejemplos de código.
©”TNGD”.com
Con los conceptos básicos explicados, es hora de ver cómo funciona BFS en la práctica. Vamos a ilustrar esto usando un gráfico con los nodos A, B, C, D, E y F, como se muestra en la imagen. El siguiente código muestra cómo implementar BFS para este gráfico usando el lenguaje de programación Python.
from collections import defaultdict, deque def bfs(graph, start): queue=deque([start])visited=set([start] ) while cola: nodo=cola.popleft() print(nodo) para el vecino en el gráfico[nodo]: si el vecino no está visitado: visitado.agregar(vecino) cola.agregar(vecino) gráfico=predeterminadodict(lista) bordes=[ (“A”,”B”),”A”,”C”), (“B”,”C”), (“C”,”D”), (“C”,”E”), (“C”,”F”), (“D”,”F”), (“E”,”F”) para borde en bordes: gráfico[borde[0]].append(borde[0]) gráfico[ edge[1]].append(edge[0]) bfs(graph,”A”)
Explicación del código
Primero, estamos importando las clases”defaultdict”y”deque”desde el módulo “colecciones”. Estos se utilizan para crear un diccionario con valores clave predeterminados y para crear una cola que permita agregar y eliminar elementos.
A continuación, estamos definiendo la función”bfs”con dos argumentos,”graph”y”comenzar”. Tomamos el argumento”gráfico”como un diccionario con los vértices como claves y los vértices vecinos como valores. Aquí, “inicio” se refiere al nodo de origen, donde comienza el algoritmo.
“queue=deque([start])” crea una cola con el nodo de origen como único elemento, y “visited=set ([inicio])” crea un conjunto de nodos visitados con el nodo de origen como único elemento.
El bucle “while” continúa hasta que la cola está vacía. “node=queue.popleft()” elimina el elemento más a la izquierda de la cola y lo almacena en la variable “node”. “print(node)” imprime estos valores de nodo.
El ciclo “for” itera sobre cada nodo vecino. “si vecino no visitado” comprueba si el vecino ha sido visitado.”visited.add(neighbor)”agrega al vecino a la lista de visitas, y”queue.append(neighbor)”agrega al vecino al extremo derecho de la cola.
Después de esto, creamos un valor predeterminado diccionario llamado”gráfico”, y definir los bordes del gráfico. El ciclo”for”itera sobre cada borde. “graph[edge[0]].append(edge[1])” agrega el segundo elemento del borde como vecino del primer elemento, y el primer elemento del borde como vecino del segundo. Esto construye el gráfico.
Finalmente, llamamos a la función”bfs”en”graph”, con el nodo fuente como”A”.
Implementación de código
Así es como se ve el algoritmo BFS cuando implementado y ejecutándose a través de un gráfico conectado.
©”TNGD”.com
En la captura de pantalla, podemos ver la salida [A, B, C, D, E F]. Esto es lo que esperaríamos ya que BFS explora los nodos en cada nivel de profundidad antes de pasar al siguiente. Volviendo al gráfico, vemos que B y C se agregarán a la cola y se visitarán primero. Se visita B y luego se agregan A y C a la cola. Como ya se visitó A, se visita C a continuación y se elimina A. Después de esto, los vecinos de C, D, E y F, se agregan a la cola. Luego se visitan y se imprime la salida.
Uso de BFS para gráficos desconectados
Usamos BFS para un gráfico conectado anteriormente. Sin embargo, también podemos usar BFS cuando los nodos no están todos conectados. Vamos a utilizar los mismos datos del gráfico, ya que el algoritmo modificado se puede ilustrar con cualquier tipo de gráfico. El código modificado es:
from collections import defaultdict, deque def bfs(graph, start): queue=deque([start]) visited=set([start]) while queue: node=queue.popleft() print (nodo) para el vecino en el gráfico[nodo]: si el vecino no está visitado: visitado.añadir(vecino) cola.agregar(vecino) para el nodo en gráfico.keys(): si el nodo no está visitado: cola=deque([nodo ]) visitado.agregar(nodo) while cola: nodo=cola.popleft() print(nodo) para vecino en gráfico[nodo]: si el vecino no está visitado: visitado.agregar(vecino) cola.agregar(vecino) gráfico=predeterminadodict(lista) bordes=[(“A”,”B”), (“A”,”C”), (“B”,”C”), (“C”,”D”), (“C”,”E”), (“C”,”F”), (“D”,”F”), (“E”,”F”)] para borde en bordes: gráfico[borde[0]]. agregar (borde [1]) gráfico [borde [1]]. agregar (borde [0]) bfs(graph,”A”)
Hemos usado un bucle”for”adicional. El ciclo itera sobre todos los nodos usando el método “graph.keys()”. BFS inicia una nueva cola si encuentra un nodo no visitado y funciona de forma recursiva. Al hacer esto, visitamos todos los nodos desconectados. Vea la imagen a continuación para ver una ilustración.
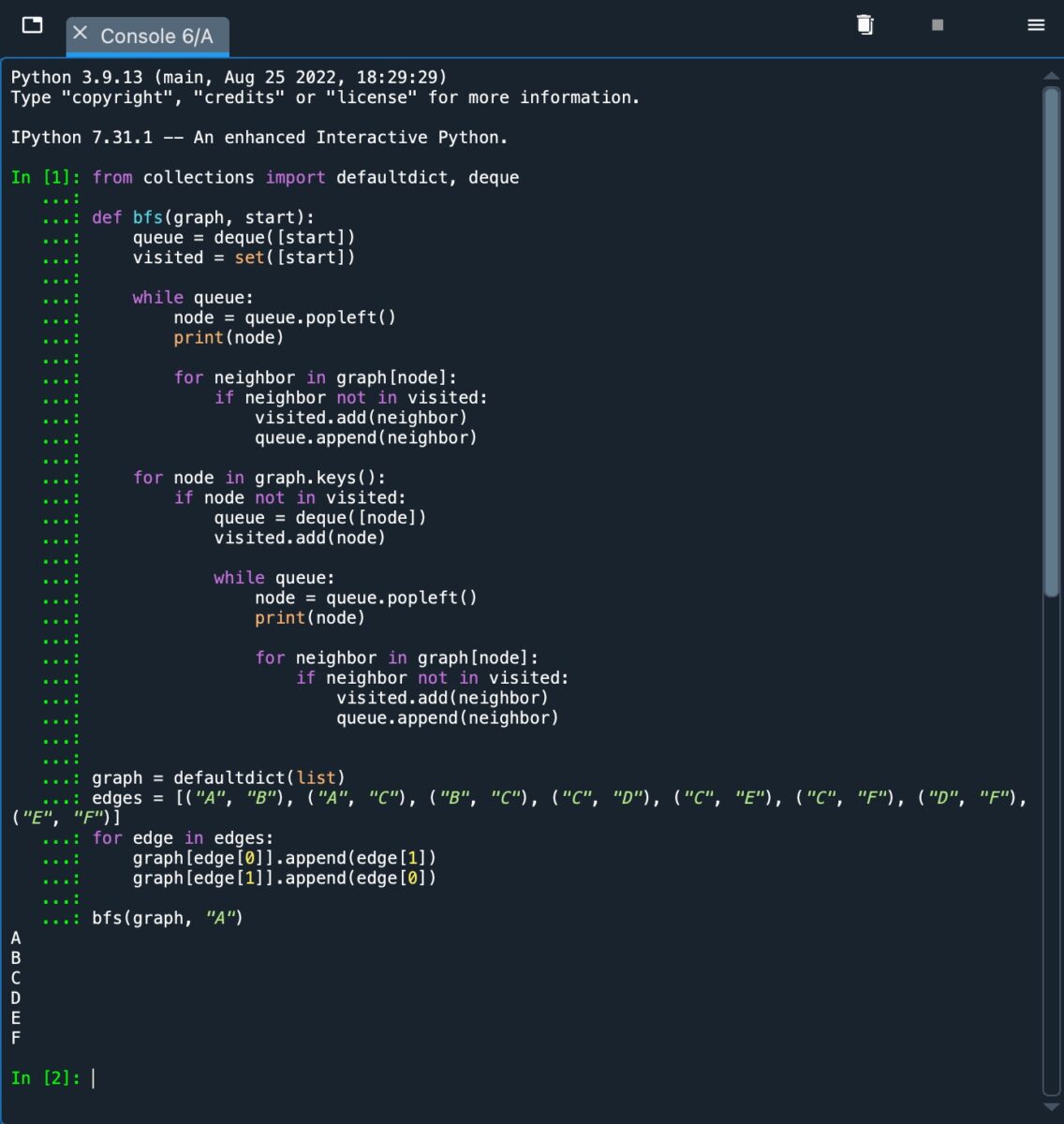Este es un ejemplo del algoritmo BFS cuando se implementa y se ejecuta a través de un gráfico desconectado.
©”TNGD”.com
Mejores y peores casos de uso para BFS
Ahora que sabemos cómo funciona BFS, debemos observar la complejidad de tiempo y espacio del algoritmo para tener una idea de sus mejores y peores casos de uso.
Complejidad de tiempo de BFS
Podemos ver que la complejidad temporal es la misma en todos los casos, y es igual a O(V + E), donde V es el número de vértices y E es el número de aristas. En el mejor de los casos, donde solo tenemos un nodo, la complejidad será O(1), porque V=1 y E=0. En el promedio y en el peor de los casos, el algoritmo visita todos los nodos a los que puede llegar desde el nodo de origen. , por lo que la complejidad depende de la estructura y el tamaño del gráfico en ambos casos.
Complejidad espacial de BFS
Nuevamente, vemos que la complejidad es la misma para todos los casos. El algoritmo visita cada nodo sin importar la estructura del gráfico. Por lo tanto, la complejidad depende de la cantidad de vértices en el gráfico.
Resumen
BFS es una forma de atravesar los nodos en un gráfico, calcular las distancias de las rutas y explorar las relaciones entre nodos. Es un algoritmo muy útil para explorar sistemas de redes y detectar ciclos de gráficos. BFS es relativamente fácil de implementar tanto para gráficos conectados como desconectados. Una ventaja es que la complejidad de tiempo y espacio es la misma para todos los casos.
Búsqueda primero en amplitud (BFS) para gráficos: explicación, con ejemplos Preguntas frecuentes (FAQ)
¿Qué es BFS?
BFS es un algoritmo que se utiliza para atravesar árboles o gráficos, generalmente aquellos que representan redes como redes sociales o informáticas. También puede detectar ciclos de gráficos o si un gráfico es bipartito, así como calcular las distancias de ruta más cortas. Primero en amplitud significa que cada nodo se explora en un nivel de profundidad particular antes de pasar al siguiente.
¿Cuál es la complejidad temporal de BFS?
La la complejidad temporal de BFS es O(V + E) en todos los casos.
¿Cuál es la complejidad espacial de BFS?
La complejidad espacial de BFS es O(V) en todos los casos.
¿Cuándo debería usar BFS?
Si necesita calcular la distancia de ruta más corta o explorar todos los vértices en un gráfico no ponderado.
¿Cómo se implementa BFS?
Por lo general, implementamos BFS utilizando una estructura de datos de cola y un conjunto para realizar un seguimiento de los nodos visitados y no visitados. El nodo de origen se agrega a la cola y se marca como visitado. Luego, el algoritmo opera recursivamente en los nodos vecinos, agregando y eliminando nodos a medida que avanza para garantizar que ningún nodo se visite dos veces.
¿Cómo se compara BFS con el algoritmo de Dijkstra?
Estos algoritmos se pueden usar para calcular las distancias de ruta más cortas, pero BFS funciona con gráficos no ponderados. Por el contrario, el algoritmo de Dijkstra funciona con gráficos ponderados.
¿Cómo se compara DFS con BFS?
Ambos se usan para recorrer un gráfico, pero difieren en como hacen esto Mientras que BFS busca cada nodo en un nivel de profundidad determinado antes de continuar, DFS visita los nodos a la mayor profundidad posible antes de volver a sí mismo para explorar otra rama. DFS generalmente usa una estructura de datos de pila en lugar de una cola.