© Oselote/Shutterstock.com
El algoritmo de clasificación de burbujas es un ejemplo de un algoritmo de clasificación simple. Este tipo de algoritmo organiza caracteres, cadenas o números en un orden específico determinado por el problema que está resolviendo con su código.
Una ordenación suele ser útil cuando desea organizar los elementos alfabéticamente o en orden numérico.. Los algoritmos de clasificación son una parte crucial de la programación, y la clasificación de burbujas es una de las favoritas entre los estudiantes debido a su simplicidad. Sin embargo, no es la mejor opción si necesita un rendimiento rápido.
Si desea obtener más información sobre el algoritmo de clasificación de burbujas y cómo funciona, está en el lugar correcto. El artículo de hoy desglosará cómo funciona el algoritmo de clasificación de burbujas y le mostrará cómo implementarlo. ¡Empecemos!
¿Qué es el algoritmo de ordenación de burbujas?
Los algoritmos de ordenación le brindan una manera de presentar los datos de forma lógica cuando ejecuta su código. Cuando está aprendiendo a programar, la clasificación de burbujas es uno de los primeros algoritmos que aprenderá porque le permite visualizar cómo funciona un algoritmo de clasificación en un nivel básico.
El algoritmo de clasificación de burbujas es único porque solo puede comparar dos conjuntos de datos adyacentes. Se mueve a través de toda la matriz, el diccionario, la lista o la cadena, compara cada elemento y ordena todo según sus requisitos.
El algoritmo
Antes de explorar cómo crear una clasificación de burbuja en su código, veamos cómo funciona paso a paso:
Primero, identificaríamos una colección de datos que necesita ordenarse. Esto puede ser una colección de números, palabras o letras que pretende organizar de una manera particular. Una función común de una ordenación de burbujas sería tomar una lista de números y ordenarlos por su valor, ya sea de menor a mayor o de mayor a menor. El algoritmo comienza en el primer elemento de una lista, que serían los datos en el índice 0 Compara esos datos con los datos en el índice 1 para determinar si es necesario un cambio. Si se realiza un cambio, tenemos un indicador que establecemos, que nos permite salir del algoritmo para hacerlo más eficiente. índice 1 al índice 2, y continúa a través de la lista hasta que llega al final. Una vez que el algoritmo ha pasado una vez, debe pasar por el proceso nuevamente porque no termina hasta que no se necesitan cambios. Esto generalmente se logra con bucles anidados que ejecutan una ordenación de burbuja a través de toda la lista hasta que un condicional, que opera en la bandera, sale una vez que hemos pasado por una iteración completa sin cambios. Una vez que esos bucles anidados se han ejecutado, la lista ordenada estar en el orden previsto para que pueda mostrarlo en la pantalla o usarlo para otras operaciones en su código.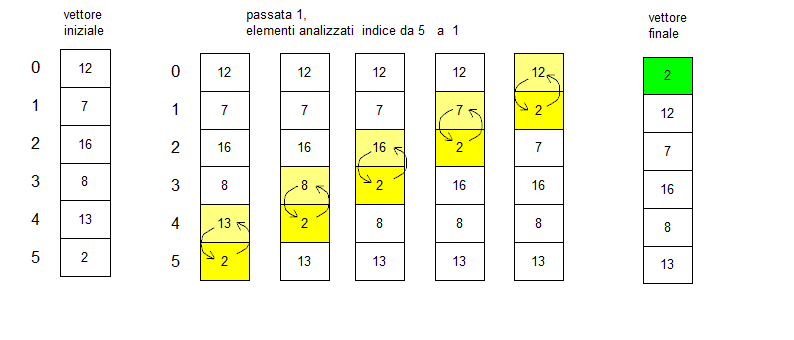 
El algoritmo de clasificación de burbujas se ilustra con un diagrama.
©Por Stefano furin – Trabajo propio, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=37141358
Funcionamiento del algoritmo Bubble Sort
Ahora que hemos cubierto la lógica del algoritmo de clasificación de burbujas, profundicemos en un ejemplo. Tomaremos una lista de números que están fuera de orden y dejaremos que la burbuja los organice en orden ascendente.
Para hacerlo simple, usaremos una lista de cuatro números:
29, 15, 0,-5
El primer cálculo que haría la ordenación de burbuja sería verificar los valores de índice 0 e índice 1 como discutimos anteriormente. Dado que 29 es mayor que 15, sus posiciones cambiarán, dándonos esta secuencia de números:
15, 29, 0,-5
A continuación, el algoritmo compara 29 y 0. Aquí está la lista resultante:
15, 0, 29,-5
La última vez en esta primera iteración, el algoritmo compara 29 con-5, dándonos esta lista:
15, 0,-5, 29
Nuestra lista no está exactamente donde necesitamos que esté, y la próxima iteración nos ayudará a resolver eso. Veremos cambiar la lista de esta forma:
0, 15,-5, 29
0,-5, 15, 29
0,-5, 15, 29
0,-5, 15, 29
Entonces la tercera iteración nos daría este resultado:
-5, 0, 15 , 29
-5, 0, 15, 29
-5, 0, 15, 29
-5, 0, 15, 29
>
Ahora, debido a que la lista está completamente ordenada, necesitaremos una forma de decirle al ciclo que deje de ejecutarse. Esto es para hacerlo más eficiente. Para hacer eso, normalmente usamos una variable booleana junto con algunas declaraciones condicionales para permitir que el algoritmo salga del bucle una vez que no se hayan realizado cambios.
Implementación del algoritmo de ordenación de burbujas usando un bucle For
Ahora, introduzcamos algo de código para el algoritmo de clasificación de burbujas en Python para obtener una buena comprensión de cómo funciona como método de clasificación. Así es como lo implementaríamos con un ciclo for:
def bubbleSort (numArray, z): for a in range(z-1): swap=False for b in range (0, z-a-1): if numArray[b] > numArray[b+1]: swap=True numArray[b], numArray[b+1]=numArray[b+1], numArray[b] si no swap: return numArray numberArray=[82, 67 , 0,-500,-80, 99, 2] x=len(matriz de números) print (“matriz ordenada:”) print (clasificación de burbujas(matriz de números, x))
Explicación del código
Desglosemos este código paso a paso para que podamos entender lo que está pasando.
Inicializar la matriz
Primero, necesitamos inicializar nuestra matriz con un conjunto de números que me gustaría ordenar (numberArray). Estos se inicializan deliberadamente en orden aleatorio para demostrar cómo funciona el algoritmo de clasificación de burbujas. A continuación, inicializamos una variable que alberga el recuento de elementos que tenemos en la matriz (x). Usaremos esta variable más adelante para controlar cuántas veces iteramos a través del bucle.
Definir el algoritmo de clasificación de burbujas
Se pasan dos valores al algoritmo, que se define como bubbleSort. El primer valor es la propia matriz. Luego también pasamos la longitud de la matriz. Dentro del algoritmo, estos se reasignan como numArray y z, respectivamente.
El ciclo que usamos para ejecutar la ordenación de burbujas iterará una cierta cantidad de veces, pero no siempre es necesario que siga su curso. Por lo tanto, primero debemos configurar una variable booleana al comienzo del ciclo for externo que cambiará de Falso a Verdadero en el ciclo interno si se realiza un intercambio durante nuestro algoritmo de clasificación.
Como hablamos anteriormente, un algoritmo de clasificación de burbujas compara dos valores adyacentes para determinar si es necesario cambiar la matriz. Entonces, configuramos un condicional para determinar qué valor es el más alto. Si el valor de la primera variable es más alto, cambiará de lugar con el elemento adyacente en la matriz. Y, dado que se ha realizado un intercambio, también estableceremos el valor booleano (intercambio) en Verdadero para que no salgamos del ciclo todavía.
Una vez que el ciclo interno haya pasado por la matriz la primera vez, el valor booleano se establecerá en True, por lo que entramos en el ciclo externo la segunda vez, configurando el valor booleano (swap) en False nuevamente para comenzar todo el proceso. Este booleano debe reinicializarse cada vez porque queremos que nuestro algoritmo pueda salir la primera vez que pasemos por el ciclo interno una vez sin un intercambio. Puede pasar por todo el proceso sin una condición de salida, pero su programa se ejecutará más rápido si se implementa.
Visitando los rangos
El algoritmo de clasificación de burbujas continuará con este proceso hasta que He pasado por una iteración completa del ciclo interno sin hacer un intercambio. En la sintaxis del ciclo for, el rango le dice al ciclo cuándo comenzar, detenerse y cuántos pasos incrementar. Puede tomar tres parámetros, pero solo necesita uno: en qué punto debe detenerse el bucle for.
En nuestro bucle for externo, solo necesitamos decirle dónde detenerse, que es en el último índice de la matriz. Tenemos que usar z-1 como el rango allí porque el índice comienza a numerarse en 0 en lugar de 1. Entonces, si dejamos en z, iría una vez más de lo necesario.
En nuestro for loop, tenemos dos parámetros porque queremos decirle dónde comenzar, en el primer índice, 0, y dónde detenerse. Nos detenemos un poco antes que el bucle for externo porque no necesitamos verificar los elementos restantes en la matriz.
Actualización de la matriz
La instrucción if crea una condición para determinar si los dos elementos adyacentes en la matriz necesitan cambiar sus posiciones. Dado que estamos clasificando los números en orden ascendente, si el primer número es mayor que el segundo número comparado, entonces ese primer número debe moverse un lugar a la derecha, lo que significa que el segundo número debe moverse un lugar a la izquierda ya que es más pequeño
Este cambio puede ocurrir de diferentes maneras, pero la forma más rápida y sencilla de hacerlo es asignar los valores a los elementos adyacentes al mismo tiempo. Esto se logra con la siguiente declaración: numArray[b], numArray[b+1]=numArray[b+1], numArray[b]. Un método alternativo sería crear una variable temporal para contener uno de los valores que deben moverse mientras el otro se mueve con una asignación simple. Pero, dado que esto requiere más código, es mucho más eficiente de lograr cuando asignamos ambos al mismo tiempo.
Resultados
Cuando el método bubbleSort sale del anidado for loops y regresa al programa principal, envía la matriz resultante a la declaración de impresión desde la que llamamos al método y muestra los resultados en la pantalla, dándonos una matriz con siete elementos ordenados en orden ascendente por valor numérico.
La matriz ordenada que obtendríamos de nuestro ejemplo:
[-500,-80, 0, 2, 67, 82, 99]
Mejores y peores casos de uso de la ordenación de burbuja Algoritmo
El algoritmo de clasificación de burbujas funciona de manera eficiente cuando tenemos un número limitado de elementos de datos que necesitamos organizar en un orden determinado. Cuando aumenta la escala o agrega demasiados puntos de datos, la ordenación de burbujas comienza a tener problemas. Si necesita un algoritmo más eficiente, hay muchas opciones. Puede buscar combinar ordenación y ordenación rápida, las cuales son significativamente más rápidas.
Veamos la complejidad de tiempo y espacio para tener una idea del rendimiento.
Complejidad de tiempo del algoritmo de clasificación de burbujas
El algoritmo de clasificación de burbujas no tiene una gran necesidad de espacio. Porque, a lo sumo, solo agregamos un valor booleano para verificar los intercambios y las variables temporales para almacenar datos mientras intercambiamos si es necesario. Por esta razón, la complejidad del espacio no cambia cuando usamos conjuntos de datos más grandes.
Conclusión
El algoritmo de ordenación de burbujas puede ser eficiente cuando solo desea ordenar pequeñas cantidades de datos. Pero realmente no es el más eficiente, y no es ideal debido a su rendimiento. En cambio, es más útil como herramienta de aprendizaje para que los programadores principiantes aprendan cómo la computadora ejecuta algoritmos. Si estás tomando un curso de estructuras de datos y algoritmos, tendrás que dominar este. Una vez que comprenda los conceptos básicos de los algoritmos de clasificación, puede pasar a otros más eficientes.
¿Qué es el algoritmo de clasificación de burbujas y cómo funciona? (Con ejemplos) Preguntas frecuentes (FAQ)
¿Qué es el algoritmo de clasificación de burbujas?
Un algoritmo de clasificación de burbujas es un algoritmo de clasificación simple que compara dos valores adyacentes y realiza un cambio basado en una condición establecida en nuestro código. Por lo general, utiliza un ciclo while o un ciclo for para iterar a través de cada conjunto de elementos adyacentes hasta que llega al final del conjunto de datos. Sin embargo, requiere más de una iteración del conjunto de datos completo para clasificar los datos en orden ascendente o descendente.
¿Cuáles son las limitaciones del algoritmo de clasificación de burbujas?
Cuando tenemos grandes conjuntos de datos, el algoritmo de clasificación de burbujas no es el mejor uso de la potencia de nuestra computadora. Otros algoritmos de clasificación serían mejores opciones porque es probable que no tomen tanto tiempo para ejecutar el algoritmo.
¿Cuál es la complejidad temporal del algoritmo de clasificación de burbujas?
La complejidad del tiempo varía de 0 (N) a 0 (N^2), donde existe el mejor de los casos cuando el conjunto de datos ya está ordenado. N representa la cantidad de elementos en el conjunto de datos, por lo que la complejidad del tiempo puede aumentar mucho cuando se trabaja con grandes colecciones de datos.
¿Cuál es la complejidad espacial del algoritmo de clasificación de burbujas?
La complejidad del espacio, sin importar cuán grande sea nuestro conjunto de datos, es O(1), lo que significa que permanece igual. En teoría, si tuviera un conjunto de datos de 200 elementos, ocuparía la misma cantidad de espacio que uno con 100.
¿Cuándo se debe usar el algoritmo de clasificación de burbujas?
Debido a que es más efectivo con pequeños conjuntos de datos, el algoritmo de clasificación de burbujas es más útil en entornos educativos, cuando los programadores principiantes están aprendiendo por primera vez a codificar algoritmos de clasificación.
Qué Cuáles son las diferentes formas de implementar el algoritmo de clasificación de burbujas?
Debido a que necesitamos iterar a través de todo el conjunto de datos para ejecutar un algoritmo de clasificación de burbujas, generalmente se implementa con bucles, ya sea un bucle for o un bucle while.
¿Cuáles son las alternativas al algoritmo de clasificación de burbujas?
Hay varios algoritmos que podemos usar para realizar una clasificación. Los siguientes son algunos de los métodos de clasificación más utilizados: clasificación por selección, clasificación por inserción, clasificación por depósito, clasificación por montón y clasificación por fusión.
By Maxwell Gaven
Ich habe 7 Jahre im IT-Bereich gearbeitet. Es macht Spaß, den stetigen Wandel im IT-Bereich zu beobachten. IT ist mein Job, Hobby und Leben.