En realidad, hay dos formas de implementar la ordenación por fusión: el enfoque de arriba hacia abajo y el enfoque de abajo hacia arriba. Es un buen momento para brindar una breve descripción general de estos procesos.
El enfoque de arriba hacia abajo
Como sugiere el nombre, este algoritmo comienza en la parte superior con la matriz inicial, divide el matriz por la mitad, ordena recursivamente estos subarreglos (es decir, dividiéndolos y repitiendo el proceso) y luego combina los resultados en una matriz ordenada.
El enfoque ascendente
Por otro lado, el enfoque ascendente se basa en un método iterativo. Comienza con una matriz de un solo elemento y luego combina los elementos de cada lado mientras los ordena. Estas matrices combinadas y ordenadas se fusionan y ordenan hasta que solo queda un elemento en la matriz ordenada. La principal diferencia es que, mientras que el enfoque de arriba hacia abajo ordena cada subarreglo de forma recursiva, el enfoque de abajo hacia arriba divide el arreglo en arreglos singulares. Luego, cada matriz se ordena y fusiona iterativamente.
Funcionamiento de Merge Sort
Después de esto, sería útil un ejemplo práctico de cómo se usa merge sort.
Digamos que tener una matriz, arr. Arr=[37, 25, 42, 2, 7, 89, 14].
Primero, verificamos si el índice izquierdo de la matriz es menor que el índice derecho. Si esto es cierto, se calcula el punto medio. Esto es igual a “(start_index” + (“end_index”-1))/2, que, en este caso, es 3. Por lo tanto, el elemento en el índice 3 es el punto medio, que es 2.
De esta forma, este arreglo de 7 elementos se ha dividido en dos arreglos de tamaño 4 y 3 para los subarreglos izquierdo y derecho respectivamente:
Array izquierdo=[37, 25, 42, 2]
Arreglo derecho=[7, 89, 14]
Continuamos calculando el punto medio nuevamente y dividiendo los arreglos en dos hasta que la división ya no sea posible. El resultado final es:
[37], [25], [42], [2], [7], [89], [14]
Y luego, puede comenzar a fusionar y ordenar estos subarreglos como tales:
[25, 37], [2, 42], [7,89], [14]
Estos subarreglos luego se fusionan y ordenados nuevamente para dar:
[2, 25, 37, 45] y [7, 14, 89]
Finalmente, estos subarreglos se fusionan y ordenan para dar el orden final array:
[2, 7, 14, 25, 37, 45, 89]
Implementación de Merge Sort
Hasta ahora, hemos cubierto cómo el algoritmo de ordenación por combinación funciona, los pasos involucrados y el trabajo detrás de él con un ejemplo. Entonces, finalmente es hora de ver cómo implementar este algoritmo usando código. Con fines ilustrativos, utilizaremos el lenguaje de programación Python. El proceso puede describirse usando el siguiente código:
def mergeSort(arr): if len(arr) > 1: mid=len(arr)//2 L=arr[:mid] R=arr[mid: ] mergeSort(L) mergeSort(R) i=j=k=0 while i len(L) y j len(R): si L[i]=R[j]: arr[k]=L[i] i +=1 else: arr[k]=R[i] j +=1 k +=1 while i len(L): arr[k]=L[i] i +=1 k +=1 while j len( R): arr[k]=R[j] j +=1 k +=1 def imprimirLista(arr): for i in range(len(arr)): imprimir(arr[i], end=””) imprimir () if__name__==’__main__’: arr=12, 11, 13, 5, 6, 7] print(“La matriz dada es”, end=”\n”) printList(arr) mergeSort(arr) print(“Ordenados array is”, end=”\n”) printList(arr)
Esto parece mucho código, pero es manejable si lo desglosamos.
Explicación de la código
Primero, estamos definiendo la función mergeSort como una función de la matriz”arr”.
La primera declaración”si”verifica si la longitud de la matriz es mayor que 1. Si es así, podemos proceder a dividir la matriz.
Luego, calculamos el punto medio de la matriz y lo dividimos en dos subarreglos,”L”y”R”.
La función mergeSort se llama recursivamente en L y R, dividiéndolos hasta que cada subarreglo solo contiene un elemento.
En este punto, tres variables se inicializan a cero=i, j y k. Los dos primeros son los índices inicial y final del subarreglo que se está operando. “k” es una variable que realiza un seguimiento de la posición actual en la matriz.
La siguiente parte, que comienza con la instrucción “while”, es la sección principal del algoritmo. El algoritmo se itera sobre L y R, comparando los elementos en i y j y copiando el elemento más pequeño a la matriz. Junto con k, estas variables de índice se incrementan, según el operador de incremento”=-“.
La siguiente sección de declaraciones”while”dicta que los elementos restantes en las dos matrices se copian en la matriz inicial.
Ya casi terminamos. A continuación, definimos la función de lista de impresión como una función de la matriz”arr”.
Por último, usamos la línea”if_name_==’_main_'”para garantizar que el código solo se ejecute cuando se ejecute el script. se ejecuta directamente, y no cuando se importa.
La matriz original se imprime como”La matriz dada es”, y la matriz ordenada final se imprime como”La matriz ordenada es”. La última línea imprime esta matriz ordenada, después de que la matriz inicial se haya combinado según el código anterior.
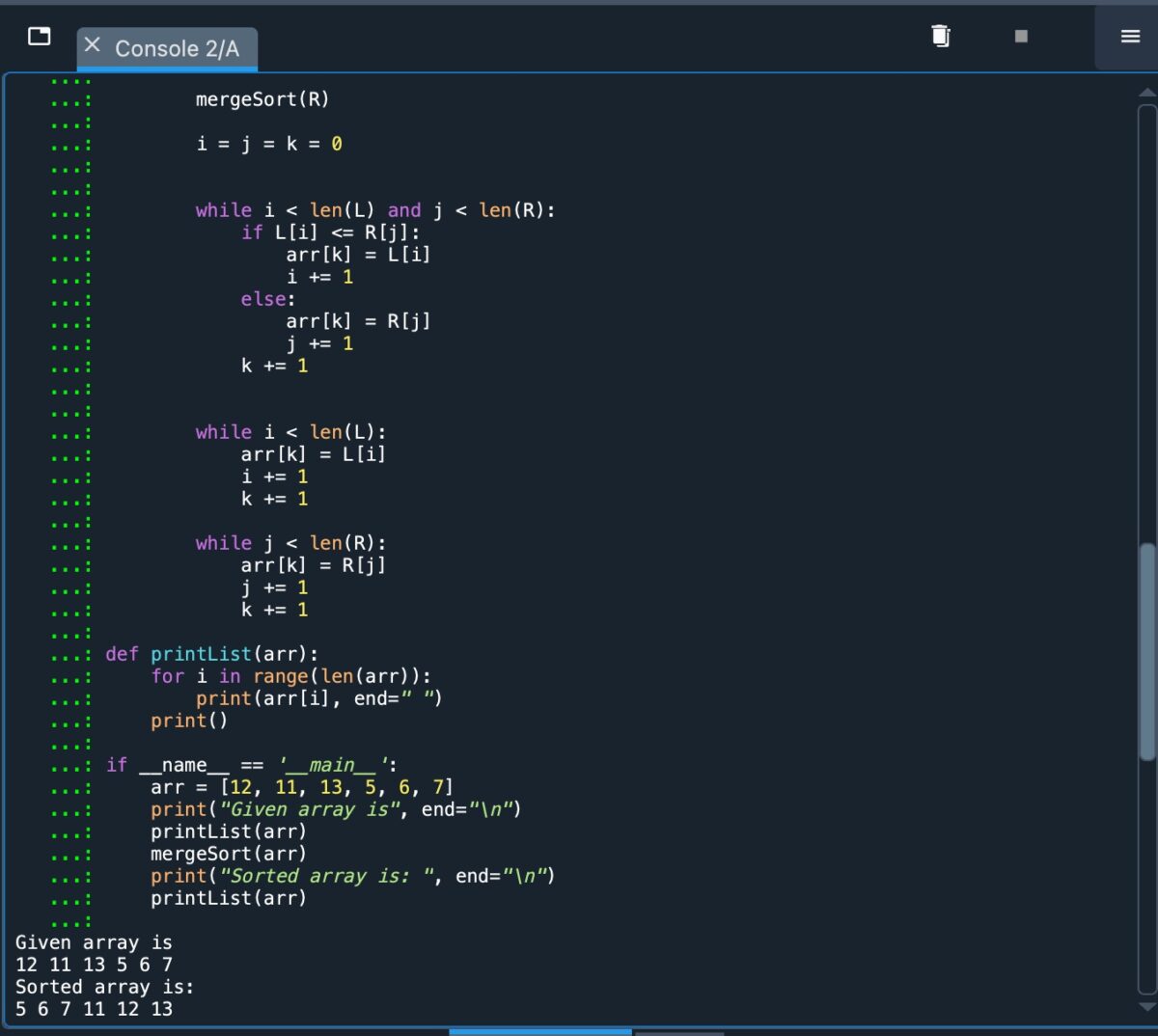
Para concluir, a continuación se muestra una captura de pantalla que muestra la implementación de este código en Python:
Código de Python para el algoritmo de clasificación por fusión.
©”TNGD”.com
Mejores y peores casos de uso de clasificación por inserción
La clasificación por fusión es un algoritmo simple, pero, como con cualquier algoritmo , tiene sus mejores casos de uso y sus peores casos. Estos se ilustran a continuación en términos de complejidad de tiempo y complejidad de espacio.
Complejidad de tiempo con clasificación por inserción
La complejidad de tiempo en cada caso se puede describir en la siguiente tabla:
El mejor de los casos se refiere a cuando la matriz está parcialmente ordenada, el caso promedio se refiere a cuando la matriz está desordenada y el peor de los casos se refiere a cuando la matriz está en orden ascendente o descendente, y desea lo contrario. Como tal, esto requeriría la mayor clasificación.
Afortunadamente, la clasificación por fusión tiene la misma complejidad de tiempo en cada caso, de O(n log n). Esto se debe a que, en cada caso, cada elemento necesita ser copiado y comparado. Esto conduce a una dependencia logarítmica del tamaño de entrada, ya que el arreglo se divide recursivamente hasta que cada subarreglo contiene un elemento. En lo que respecta a los algoritmos de clasificación, la complejidad temporal de la clasificación por combinación es mejor que la de otros, como la clasificación por inserción y la clasificación por selección. Como tal, la clasificación por fusión es uno de los mejores algoritmos de clasificación para trabajar con grandes conjuntos de datos.
A continuación, examinaremos la complejidad espacial de la clasificación por fusión.
Complejidad espacial de la clasificación por fusión
En comparación con otros algoritmos de ordenación, la complejidad espacial de la ordenación por fusión no funciona tan bien Esto se debe a que, en lugar de una complejidad de O(1) (donde el uso de la memoria es constante y solo se almacena una variable temporal), la ordenación por combinación tiene una complejidad de espacio de O(n), donde n es el tamaño de entrada. En el peor de los casos, se deben crear n/2 matrices temporales, cada una con un tamaño de n/2. Esto significa que hay un requisito de espacio de O(n2/4) u O(n2). Pero, en el promedio y en el mejor de los casos, la cantidad de arreglos necesarios es log(n) base 2, lo que significa que la complejidad es proporcional a n. En general, la complejidad de la ordenación por combinación es relativamente buena y el algoritmo es adecuado para grandes conjuntos de datos, pero el uso de la memoria es más significativo que otros métodos.
Conclusión
En conclusión, Se han explicado las ventajas y desventajas del algoritmo de ordenación por combinación, junto con cómo funciona el algoritmo, ilustrado con ejemplos. Merge sort es un algoritmo de clasificación adecuado para grandes conjuntos de datos, incluso si su uso de memoria es relativamente alto. En resumen, es un algoritmo relativamente simple de entender y excelente para implementar en muchos entornos.