© whiteMocca/Shutterstock.com
Los algoritmos de clasificación generalmente se dividen en dos campos: fáciles de implementar o más rápidos de ejecutar. La ordenación rápida cae principalmente en la última categoría. Continúe leyendo para descubrir cómo implementar este algoritmo y las mejores situaciones para usarlo.
¿Qué es la clasificación rápida?
La clasificación rápida es un algoritmo de clasificación que se utiliza para organizar matrices de datos. Se basa esencialmente en el principio conocido como divide y vencerás. Este es el método por el cual dividimos un problema más grande y complejo en subproblemas más simples. Estos subproblemas luego se resuelven y las soluciones se combinan para encontrar la solución al problema original.
El algoritmo detrás de la ordenación rápida
Esto no es exactamente cómo implementar la ordenación rápida, pero da una idea de cómo funciona.
//i-> Índice inicial, j–> Índice final Quicksort(array, i, j) { if (i j) { pIndex=Partition(A, i, j) Quicksor(A,i, pIndex-1) Quicksort(A,pIndex+1, end) } }
Primero, definimos el ordenamiento rápido como una función de una matriz con un elemento inicial y un elemento final. La declaración”si”verifica que la matriz tenga más de un elemento.
En este caso, llamamos a la función”partición”, que nos da el índice del elemento”pivote”. Esto separa la matriz en dos subarreglos, con elementos más pequeños y más grandes que el pivote respectivamente.
La función se llama recursivamente en cada subarreglo, hasta que cada subarreglo solo tiene un elemento. Luego se devuelve la matriz ordenada y se completa el proceso.
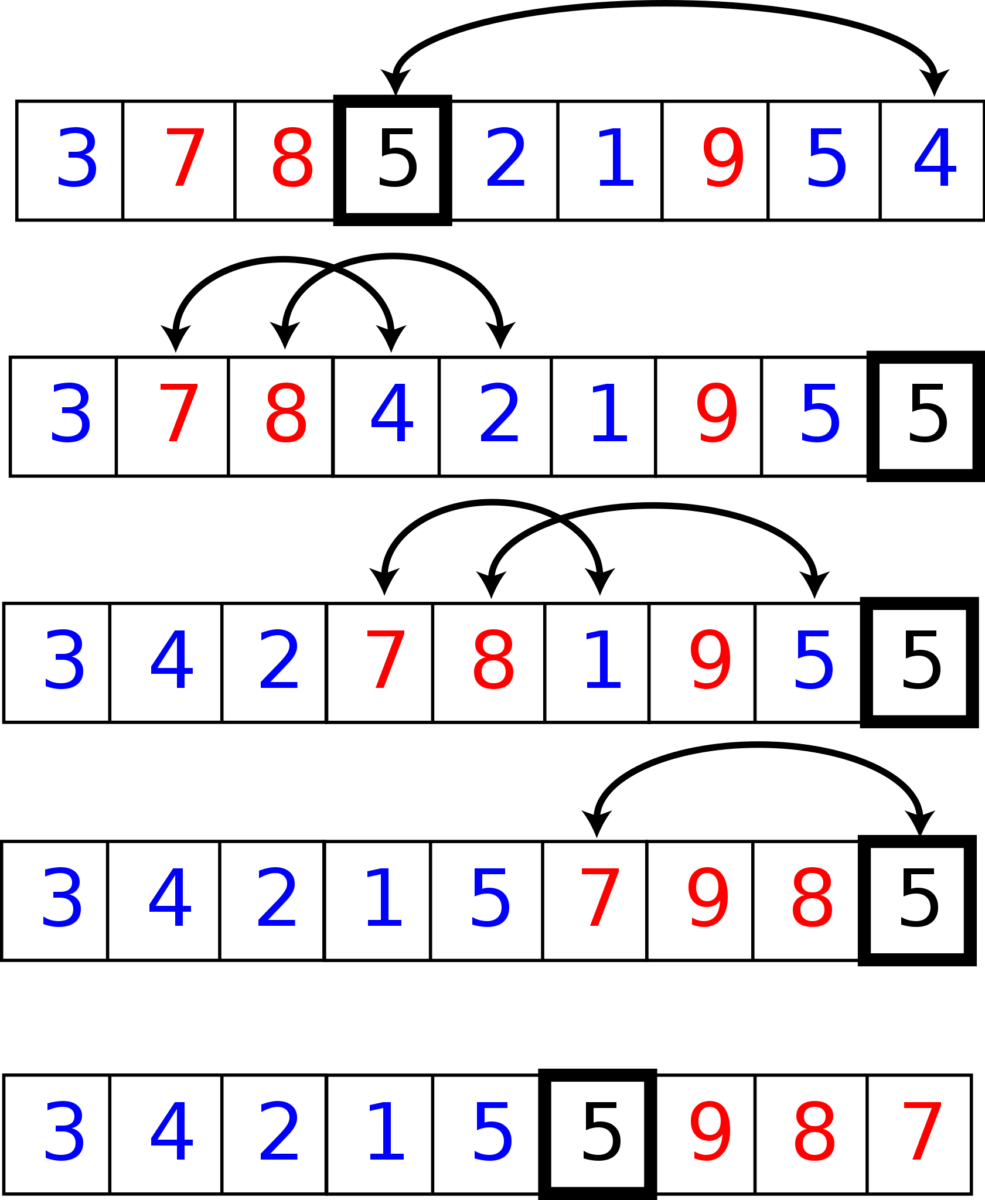 En este ejemplo, el elemento encuadrado es el elemento pivote, los elementos azules son iguales o más pequeños y los elementos rojos son mayores.
En este ejemplo, el elemento encuadrado es el elemento pivote, los elementos azules son iguales o más pequeños y los elementos rojos son mayores.
©Dcoetzee/Public Domain – Licencia
Un ejemplo de clasificación rápida
Como con la mayoría de las cosas, rápido ordenar se explica mejor usando un ejemplo para ilustrar.
Tomemos la siguiente matriz: [56, 47, 98, 3, 6, 7, 11]
Tenemos índices del 0 al 6 (recuerde que el primer elemento es el índice 0, no el 1).
Tomando el último elemento como el pivote, la matriz se reorganiza para que los elementos más pequeños que el pivote estén a la izquierda, y los elementos más grandes están a la derecha. Esto se hace inicializando las variables i y j a 0. Si arr[j], o el elemento actual, es más pequeño que el pivote, lo intercambiamos con arr[i] y lo hacemos de forma incremental. Luego, el pivote se intercambia con arr[i] para que este elemento esté en su posición ordenada.
Esto da los subarreglos [6, 7, 3] y [56, 47, 98]. El índice del elemento pivote ahora es 3 en lugar de 6.
Se llama a la ordenación rápida, que ordena el subarreglo izquierdo alrededor del elemento pivote, 3, ordenando los subarreglos [6] y [7].
Luego llamamos a la ordenación rápida recursivamente en el subarreglo derecho, de modo que se clasifique en [47, 56, 98].
Finalmente, los subarreglos se combinan para dar el arreglo ordenado: [3, 6, 7, 11, 47, 56, 98].
Implementación
Ahora que hemos cubierto la base detrás del ordenamiento rápido, implementémoslo usando Python. El código que usamos puede describirse como tal:
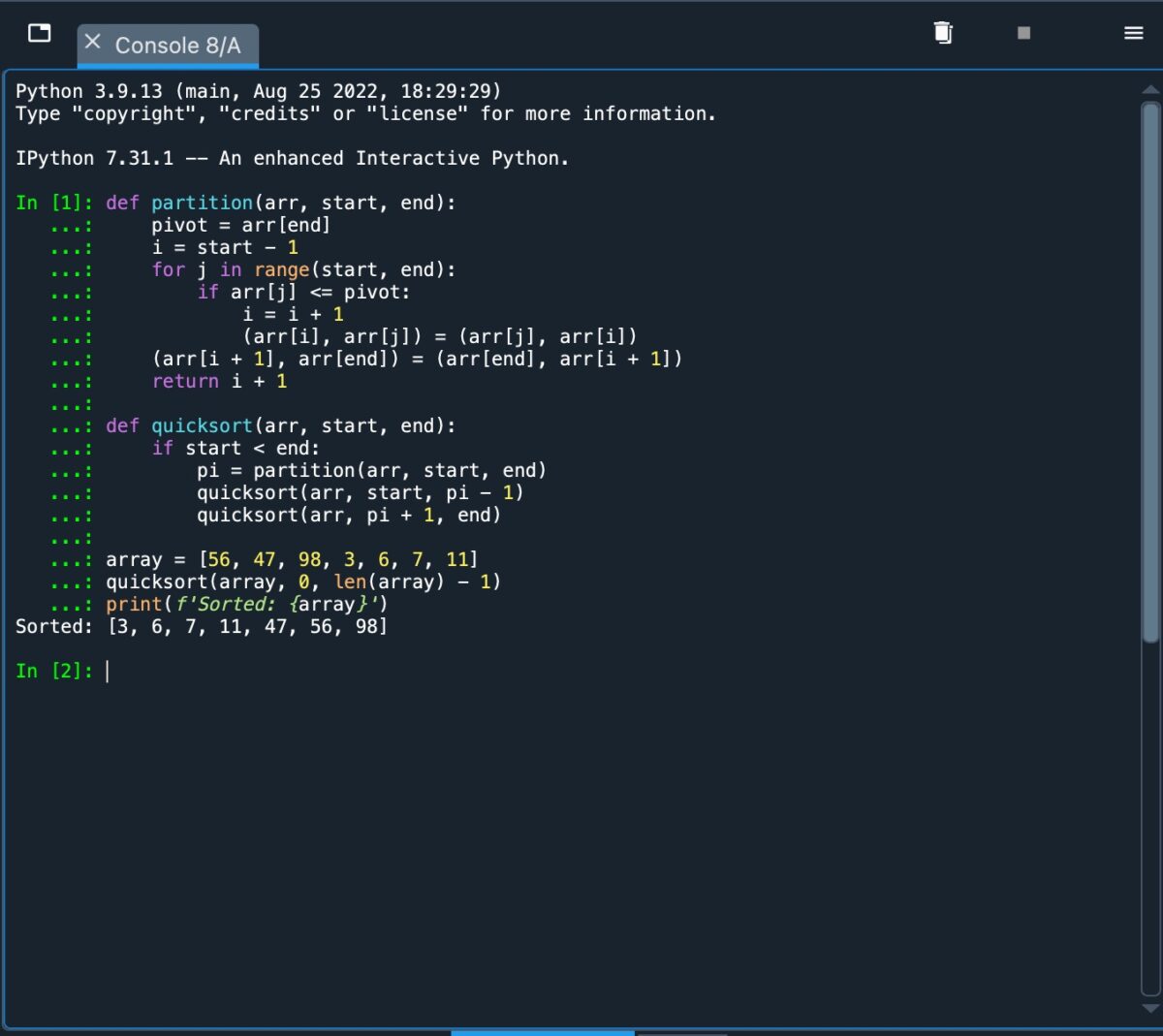
def partición(arr, inicio, final): pivote=arr[final] i=inicio-1 for j in range(inicio, final): if arr[j]=pivote: i=i + 1 (arr[i], arr[j]=(arr[j], arr[i]) (arr[i + 1], arr[fin])=(arr[fin], arr[i + 1]) return i + 1 def ordenaciónrápida(arr, inicio, fin): if inicio fin: pi=partición(arr, inicio, fin) ordenaciónrápida(arr, inicio, pi-1) ordenaciónrápida(arr, pi + 1, fin) matriz=[56, 47, 98, 3, 6, 7, 11] ordenación rápida (matriz, 0, len (matriz)-1) impresión (f’Ordenado: {matriz}’)
Primero , estamos definiendo una función de partición como una función de una matriz, con un índice inicial y final.
El valor de pivote se establece en el último elemento de la matriz, y i se inicializa al inicio índice, menos 1.
El bucle”for”itera sobre la matriz, desde el índice inicial hasta el índice final menos 1.
La declaración”if”intercambia el elemento actual, j, con el valor en el índice i si j es menor que o eq ual al pivote. Luego se incrementa la variable i.
Después de esto, el pivote se intercambia con el elemento en el índice i+1. Esto significa que todos los elementos a la izquierda del pivote son menores o iguales que él, y los elementos a la derecha son mayores que él.
Entonces se devuelve el índice del valor del pivote.
“Quicksort” se define como una función de la matriz, y la matriz se verifica para asegurarse de que tiene más de un elemento.
Luego se llama a la función de “partición”, con el índice valor establecido en”pi”. La ordenación rápida se llama recursivamente en los subarreglos izquierdo y derecho, hasta que cada subarreglo solo contiene un elemento.
Finalmente, se crea un arreglo ordenado y se imprime usando la función”imprimir”.
 La ordenación rápida se llama recursivamente a la izquierda y los subarreglos correctos, hasta que cada subarreglo solo contenga un elemento.
La ordenación rápida se llama recursivamente a la izquierda y los subarreglos correctos, hasta que cada subarreglo solo contenga un elemento.
©”TNGD”.com
Mejores y peores casos de uso de clasificación rápida
Si bien la teoría detrás de la clasificación rápida puede Parece complicado al principio, el algoritmo tiene muchas ventajas y generalmente es bastante rápido. Echemos un vistazo a la complejidad temporal y espacial de la ordenación rápida.
Complejidad temporal de la ordenación rápida
La tabla resume la complejidad temporal de la ordenación rápida.
El mejor caso es cuando la partición está equilibrada, donde el pivote está cerca o es igual al valor medio. Como tal, ambos subarreglos tienen un tamaño similar y se realizan n operaciones en cada nivel. Esto lleva a una complejidad de tiempo logarítmica.
Cuando el elemento pivote está relativamente cerca, este es el caso promedio. La complejidad del tiempo es la misma que en el mejor de los casos, ya que las matrices tienen aproximadamente el mismo tamaño.
Sin embargo, el peor de los casos convierte la complejidad del tiempo en tiempo cuadrático. Esto se debe a que la matriz está muy desequilibrada, donde el pivote está cerca del elemento mínimo o máximo. Esto provoca una situación en la que los subarreglos tienen un tamaño muy desigual, y uno contiene solo un elemento. Como tal, hay n niveles de recursividad, así como n operaciones, lo que lleva a una dependencia cuadrática del tamaño de entrada.
Complejidad espacial de ordenación rápida
Otro factor a considerar es el espacio complejidad de tipo rápido. Esto se puede resumir así:
La complejidad del espacio para la ordenación rápida es la misma para el mejor y el promedio casos. Esto se debe a que el algoritmo tiene log n niveles recursivos, y cada llamada recursiva usa una cantidad constante de espacio de memoria. Como tal, el espacio de memoria total es proporcional a la profundidad del árbol de recursividad.
Sin embargo, en el peor de los casos, la complejidad del espacio cambia a O(n). Debido a que el árbol de recurrencia está significativamente desequilibrado, lo que significa que hay n llamadas recursivas.
Conclusión
En general, la ordenación rápida es, como sugiere el nombre, una forma muy eficiente de ordenar una matriz, particularmente los grandes. Una vez que se comprende el proceso, es relativamente fácil de implementar y modificar. Es útil en una amplia gama de escenarios y funciona como una buena base para algoritmos de clasificación más complejos.
A continuación…
¿Qué es la clasificación rápida y cómo funciona? (Con ejemplos) Preguntas frecuentes (FAQ)
¿Qué es la clasificación rápida?
La clasificación rápida es un algoritmo de clasificación para clasificar matrices de datos. Funciona seleccionando un elemento pivote y dividiendo la matriz en dos subarreglos, uno con elementos más pequeños que el pivote y otro con elementos más grandes. Este proceso se repite recursivamente hasta que cada subarreglo se ordena y contiene solo un elemento. Luego, las matrices se combinan para dar una matriz ordenada.
¿La ordenación rápida es un algoritmo estable?
La ordenación rápida suele ser un algoritmo inestable. Esto significa que es posible que el orden relativo de elementos iguales no se conserve en el resultado final.
¿Cómo se elige el elemento pivote con clasificación rápida?
Puede elegir el primer o el último elemento, o hacer una elección aleatoria. Con conjuntos de datos especialmente grandes, aleatorizar la elección generalmente conduce a un buen rendimiento.
¿Cuál es la complejidad temporal de la ordenación rápida?
El mejor caso y el promedio es O(n log n), mientras que el peor de los casos es O(n2).
¿Cuál es la complejidad del espacio de clasificación rápida?
La mejor y los casos promedio son O(log n), mientras que el peor de los casos es O(n).
¿Cuáles son los mejores casos para usar ordenación rápida?
La ordenación rápida se puede usar para muchos tipos de matrices, pero a veces, las alternativas como la ordenación en montón o la ordenación por combinación pueden funcionar mejor, dadas ciertas restricciones. Por lo general, aquí es donde necesita un algoritmo estable como la ordenación por combinación, o donde el tiempo es un factor. Por ejemplo, la complejidad de tiempo del caso más desfavorable de la ordenación en montón es tan buena como la complejidad de tiempo de caso promedio para la ordenación rápida. Los algoritmos más simples, como la selección o la ordenación por inserción, también pueden ser más rápidos para conjuntos de datos pequeños.