© Song_about_summer/Shutterstock.com
Lors de la recherche dans des graphiques ou des structures de données arborescentes, deux algorithmes populaires sont Depth-First Search (DFS) et Breadth-First Search (BFS). Les deux ont le même objectif de trouver un chemin ou de parcourir un graphe ; cependant, DFS et BFS diffèrent en termes d’approche et d’efficacité.
DFS est récursif, traverse profondément le graphique et revient en arrière lorsqu’il atteint des impasses, tandis que BFS visite de manière itérative tous les nœuds adjacents avant d’avancer. Cet article mettra en contraste DFS et BFS en décrivant les principales différences ainsi que les avantages et les inconvénients associés à chaque approche.
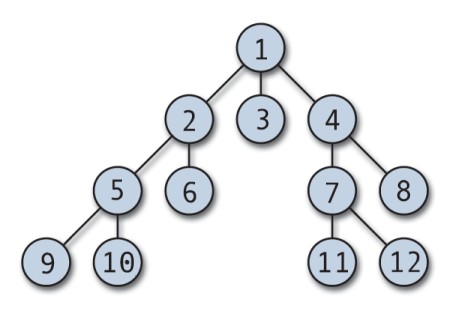
L’algorithme DFS recherchera aussi loin que possible dans chaque branche avant de revenir en arrière.
©Wolfram Esser/CC BY-SA 3.0-Licence
Complexité temporelle et spatiale
Une autre différence significative entre DFS et BFS est leur complexité spatio-temporelle. La complexité temporelle de DFS est O(V+E), où V est le nombre de sommets et E est le nombre d’arêtes dans un graphe ou un arbre. De plus, sa complexité spatiale dépasse également O(V+E) puisque tous les nœuds visités doivent être stockés sur une pile jusqu’à atteindre leurs feuilles respectives.
Contrairement, BFS a une complexité temporelle de O(V+E) , similaire à DFS ; cependant, sa complexité spatiale est O(V), car il stocke tous les nœuds visités dans un tableau. Par conséquent, BFS peut nécessiter plus de mémoire que DFS lorsqu’il s’agit de grands graphiques ou d’arbres.
Cas d’utilisation et applications
DFS et BFS ont des utilisations et des applications distinctes. DFS est souvent utilisé lorsque l’espace de recherche est large et profond, l’objectif étant d’explorer aussi loin qu’avant le retour en arrière. Cela peut également être bénéfique lorsque vous essayez de trouver une solution dans des jeux ou des puzzles où la réponse peut être située au plus profond de l’espace du puzzle.
BFS, d’autre part, est souvent utilisé lors de la recherche d’un grand et espace de recherche peu profond pour identifier le chemin le plus court entre deux nœuds ou sommets. Il détermine également la distance la plus proche entre deux nœuds de réseau ou emplacements sur une carte géographique.
Exhaustivité et Optimalité
Les algorithmes de recherche doivent répondre à deux exigences essentielles : l’exhaustivité et l’optimalité. L’exhaustivité indique si l’algorithme peut garantir la recherche d’une solution s’il en existe une, tandis que l’optimalité implique de trouver le chemin le plus court ou le plus optimal vers cette solution.
DFS n’est pas parfait ou optimal, car il peut rester bloqué dans un boucle infinie ou échouer à trouver le chemin le plus court. DFS peut se bloquer si un cycle de son graphique ou de son arbre ne parvient pas à suivre les nœuds visités. De plus, DFS peut trouver des chemins sous-optimaux pour résoudre des problèmes.
Cependant, BFS est complet et optimal. Il garantit de trouver une solution s’il en existe une, ainsi que de trouver le chemin le plus court. Après avoir exploré tous les nœuds à un niveau de profondeur avant de passer à un autre, BFS s’assure qu’il trouve le chemin le plus court. Néanmoins, BFS peut prendre plus de temps que DFS dans certains cas, en particulier lorsqu’il s’agit de graphiques ou d’arbres profonds ou étroits.
Gestion de la mémoire
Un autre facteur crucial lors du choix entre DFS et BFS est la mémoire. gestion. La gestion de la mémoire fait référence à la façon dont un algorithme utilise la mémoire et à la quantité d’espace nécessaire pour stocker les nœuds visités.
DFS utilise une pile pour stocker les nœuds visités, mais de grands espaces de recherche ou des graphiques peuvent causer des problèmes. Dans de tels cas, DFS peut manquer de mémoire et ne pas trouver de solution optimale ; les graphiques ou les arbres denses nécessitent plus de mémoire en raison des cycles fréquents.
BFS s’appuie sur une structure de données de file d’attente pour stocker les nœuds visités, garantissant qu’il ne manque pas de mémoire. Cependant, dans certaines circonstances, BFS peut utiliser plus de mémoire que DFS, en particulier lorsque le graphe ou l’arbre est large et peu profond ou comporte de nombreuses branches. BFS peut également nécessiter plus de ressources s’il y a de nombreux nœuds ou si la structure est clairsemée.
 Un algorithme BFS recherche tous les nœuds à une profondeur avant de passer aux nœuds à la profondeur suivante.
Un algorithme BFS recherche tous les nœuds à une profondeur avant de passer aux nœuds à la profondeur suivante.
©Alexander Drichel/CC BY-SA 3.0 – Licence
Complexité de la mise en œuvre
La complexité de la mise en œuvre d’un algorithme fait référence à la facilité ou à la difficulté de son exécution. Cela dépend du langage de programmation utilisé, des structures de données disponibles et de toute logique nécessaire pour une exécution réussie.
DFS est généralement plus facile à mettre en œuvre que BFS car il n’a besoin que d’une structure de données de pile et d’une fonction ou d’une boucle récursive. DFS peut être mis en œuvre à l’aide d’un algorithme de recherche en profondeur simple qui visite chaque nœud avant d’explorer chaque branche à tour de rôle. De plus, il est plus simple à mettre en œuvre dans les langages de programmation récursifs tels que Python, où la récursivité vient naturellement.
BFS, sur d’autre part, nécessite une structure de données de file d’attente et une boucle. Pour l’implémenter efficacement, BFS utilise un algorithme de recherche en largeur qui visite tous les nœuds à une profondeur avant de passer au suivant. Cependant, l’implémentation de BFS dans des langages de programmation récursifs comme Python peut être plus difficile car ils nécessitent une vraie boucle plutôt qu’une simple récursivité.
Applications
DFS et BFS ont des applications distinctes dans divers domaines. DFS est couramment utilisé dans l’infographie, l’intelligence artificielle et l’exploration Web pour proposer des modèles et des images 3D en explorant l’espace 3D pour restituer des objets. L’intelligence artificielle utilise DFS pour les arbres de décision ou les arbres de jeu-évaluant chaque mouvement possible pour explorer les branches de l’arbre-tandis que les robots d’exploration Web utilisent DFS pour explorer le Web et explorer les liens sur les pages.
BFS a été largement utilisé dans le réseau routage, algorithmes de chemin le plus court et puzzles. Dans le routage réseau, il trouve le chemin le plus court entre deux nœuds en explorant tous les chemins potentiels jusqu’à trouver le plus court. BFS joue également un rôle dans les algorithmes de chemin le plus court comme Dijkstra ou A* qui garantit de trouver le chemin le plus court ; de même, lors de la résolution d’énigmes telles que Rubik’s Cube à l’aide de BFS, vous devez déterminer la solution la plus courte qui résout l’énigme.
 L’utilisation de BFS pour résoudre le Rubik’s Cube déterminera la solution la plus rapide pour résoudre le puzzle.
L’utilisation de BFS pour résoudre le Rubik’s Cube déterminera la solution la plus rapide pour résoudre le puzzle.
©gd_project/Shutterstock.com
Espace de recherche
L’espace de recherche est l’ensemble de tous les états ou configurations possibles qu’un algorithme peut explorer pour trouver sa solution. Il peut être représenté sous la forme d’un graphique ou d’un arbre, où chaque nœud représente un état ou une configuration, et chaque arête signifie une transition entre eux.
DFS étudie l’espace de recherche en profondeur d’abord, explorant chaque branche aussi loin que possible avant de revenir en arrière et d’explorer d’autres branches. Cette approche fonctionne mieux pour les espaces de recherche vastes et profonds où la solution peut se trouver en profondeur. Malheureusement, DFS peut rester bloqué dans une boucle infinie si une boucle infinie est présente et qu’il ne garde pas une trace des nœuds visités.
BFS parcourt l’espace de recherche d’abord en largeur, explorant tous les nœuds à la fois profondeur avant de passer au suivant. Il est idéal pour les espaces de recherche larges ou peu profonds où la solution peut être proche de la racine. BFS garantit de trouver le chemin le plus court vers cette solution mais peut prendre plus de mémoire et être plus lent dans certains cas que DFS.
Stratégie de recherche
Une stratégie de recherche fait référence à un algorithme qui décide quel nœud à explorer ensuite. Des facteurs tels que le coût, l’heuristique ou le caractère aléatoire peuvent guider ce processus de prise de décision.
DFS utilise une stratégie de recherche en profondeur d’abord, dans laquelle il explore chaque branche dans la mesure du possible avant de revenir et d’explorer d’autres branches. DFS n’utilise aucun coût ou heuristique lors de la sélection du nœud à explorer ensuite ; ainsi, il peut explorer des chemins sous-optimaux. Dans certains cas, DFS peut également s’appuyer sur le caractère aléatoire, comme Monte Carlo Tree Search.
BFS utilise généralement une stratégie de recherche en largeur d’abord, explorant tous les nœuds à une profondeur avant de passer au suivant. À l’inverse, il utilise une stratégie de recherche de coût uniforme qui donne la priorité aux nœuds avec le coût le plus bas. Dans certains cas, BFS peut également s’appuyer sur des heuristiques comme l’algorithme A*, qui utilise le coût et la distance estimée pour décider quel nœud explorer ensuite.
DFS vs BFS : 10 faits à connaître
DFS signifie Depth First Search, tandis que BFS signifie Breadth First Search.DFS traverse un graphique ou un arbre dans un mouvement en profondeur, tandis que BFS se déplace en fonction de la largeur de l’arbre.Pour suivre les nœuds visités pendant la traversée DFS, ils utilisent une pile, tandis qu’avec BFS, il utilise une file d’attente. DFS peut être utilisé pour le tri topologique, la détection de cycle et la recherche de composants fortement connectés dans les graphiques ; tandis que BFS vise à trouver le chemin le plus court entre deux nœuds.DFS prend moins de place, tandis que BFS en nécessite plus car il stocke tous les nœuds au niveau actuel avant de passer au suivant.DFS est plus rapide lors de la résolution de problèmes impliquant un grand nombre de nœuds, tandis que BFS excelle lorsqu’il s’agit de groupes plus petits. DFS traverse tous les nœuds d’un graphique ou d’un arbre, tandis que BFS ne visite que ceux qui se trouvent le long du chemin le plus court. trouver le chemin le plus court, alors que BFS le fait toujours. De plus, DFS pourrait rester coincé dans une boucle infinie si votre graphique contient des cycles ; cependant, BFS se termine toujours lorsqu’il ne reste que des nœuds finis.
DFS ou BFS : lequel est le meilleur ?
Les algorithmes de recherche en profondeur (DFS) et de recherche en largeur (BFS) possèdent chacun leurs propres avantages et inconvénients, ce qui en fait un algorithme mieux adapté à certains scénarios que l’autre.
DFS traverse efficacement des graphes profonds ou infinis avec une faible complexité spatiale et une implémentation basée sur la récursivité. Il détecte également efficacement les cycles dans un graphique puisqu’il explore le plus loin possible le long de chaque branche avant de revenir en arrière. DFS fournit des solutions à des problèmes tels que la recherche de composants connectés, le tri topologique et le 8-puzzle ; des modifications sont possibles.
Inversement, BFS est plus adapté pour trouver le chemin le plus court entre deux nœuds dans un graphe, car il examine tous les nœuds à cette profondeur avant de passer au niveau suivant. De plus, il peut être utilisé pour calculer l’arbre couvrant minimum d’un graphe et résoudre des problèmes comme Knight’s Tour.
Les deux algorithmes ont leurs propres complexités temporelles, et le choix entre eux dépend du problème particulier et caractéristiques du graphique analysé. De manière générale, BFS a une complexité temporelle plus élevée que DFS mais garantit le chemin le plus court entre deux nœuds dans un graphe non pondéré ; d’autre part, DFS peut avoir une complexité moindre mais ne garantit pas toujours ce chemin le plus court.
En conclusion, le choix entre DFS et BFS dépend du problème à résoudre et du graphe analysé. Les deux algorithmes ont leurs forces et leurs faiblesses ; par conséquent, comprendre les deux peut aider à sélectionner celui qui convient le mieux à un problème spécifique. Il est donc essentiel d’avoir les deux types d’algorithmes dans votre boîte à outils, ainsi que des exemples dans lesquels ils sont les plus bénéfiques.
DFS vs BFS : comparaison complète et FAQ sur les 9 différences clés (Foire aux questions)
Quel algorithme est le meilleur pour trouver un chemin entre deux nœuds ?
BFS et DFS peuvent être utilisés pour trouver un chemin entre deux nœuds. BFS est meilleur pour trouver la route la plus courte, tandis que DFS préfère trouver des chemins qui ne sont peut-être pas les plus courts mais qui peuvent avoir d’autres caractéristiques souhaitables comme être de type topologique ou de composant fortement connecté.
Quel algorithme est mieux pour parcourir un graphe clairsemé ?
BFS est supérieur pour parcourir un graphe clairsemé car il explore tous les nœuds à un niveau avant de continuer, ce qui le rend efficace lorsqu’il y a peu d’arêtes. Au contraire, DFS peut explorer de nombreux nœuds non liés, ce qui le rend moins efficace lorsqu’il travaille dans des graphes clairsemés.
Quel algorithme est le meilleur pour parcourir un graphe dense ?
DFS est plus efficace lors de la traversée d’un graphe dense, car il explore les nœuds en profondeur et peut rapidement revenir à ceux qui sont toujours pertinents pour la recherche. Cependant, BFS peut sonder plusieurs nœuds non pertinents à la fois avant d’atteindre le nœud souhaité, ce qui le rend moins efficace dans les réseaux denses.
DFS et BFS peuvent-ils être utilisés pour trouver les composants connectés d’un graphe ?
Oui, DFS et BFS peuvent être utilisés pour découvrir les composants connectés d’un graphe. DFS commence à partir d’un nœud et traverse aussi loin que possible avant de revenir et d’explorer d’autres nœuds non visités, tandis que BFS examine tous les nœuds à un niveau avant de passer au suivant.
DFS et BFS peuvent-ils être utilisés pour détecter des cycles dans un graphique ?
Oui, DFS et BFS peuvent être utilisés pour détecter des cycles dans des graphiques. DFS détecte les cycles en gardant une trace des nœuds visités dans une liste et une pile de nœuds explorés ; si ce même nœud réapparaît sans être son parent dans aucun des deux ordres, il est alors considéré comme un nouveau cycle. De même, BFS maintient à la fois des listes de nœuds visités et une file d’attente active de nœuds explorés ; si un nœud précédemment visité réapparaît sans être son propre enfant dans cette dernière file d’attente, il est signalé comme potentiellement dommageable.
DFS et BFS peuvent-ils être utilisés pour trouver la sorte topologique d’un graphe acyclique orienté ( DAG) ?
Oui, DFS et BFS peuvent être utilisés pour déterminer le type topologique d’un DAG. Avec DFS, cela se fait en maintenant un index des nœuds visités ainsi qu’une pile continue de ceux qui sont explorés. Une fois que tous les enfants de chaque nœud ont été explorés, ils sont ajoutés au tri topologique ; de même, dans BFS, il existe également un index gardant une trace des nœuds visités ainsi qu’une file d’attente en cours qui attend l’exploration ; lorsque tous les parents d’un nœud ont été explorés, il est également inclus dans le tri topologique.
DFS et BFS peuvent-ils être utilisés pour trouver le chemin le plus court dans un graphe pondéré ?
BFS peut être utilisé pour trouver le chemin le plus court dans un graphe non pondéré, tandis que l’algorithme de Dijkstra est utilisé pour les graphes pondérés. Cependant, DFS peut également réussir lorsque les pondérations ne sont pas négatives et que la recherche est limitée à un composant connecté.