© BEST-BACKGROUNDS/Shutterstock.com
Il existe de nombreuses applications pour les listes chaînées, telles que le traitement de la musique et des images et la représentation de graphiques, d’arbres et de structures de données plus élaborées. Mais pourquoi voudriez-vous inverser une liste chaînée ? Allons-y.
Qu’est-ce qu’une liste chaînée inversée ?
Comme vous pouvez probablement le deviner, c’est une liste chaînée qui a… été inversée ! Normalement, chaque nœud pointe vers le nœud suivant dans une liste, en commençant par le nœud principal et en terminant par le nœud final. Mais, lorsque vous inversez une liste chaînée, les pointeurs sont inversés, de sorte que la tête devient la queue et la queue devient la tête. Considérons le cas simple d’une liste à 5 nœuds. Cela ressemblerait normalement à ceci :

head → node1 → node2 → node3 → node4 → node5 → tail
une fois qu’on inverse la liste, on obtient :
tail → node5 → node4 → node3 → node2 → node1 → head
Même si la liste devient plus longue et implique plus de valeurs de données, le principe reste le même.
Pourquoi voudriez-vous inverser un Liste chaînée ?
Puisqu’une liste chaînée inversée est toujours une liste chaînée, par essence, beaucoup d’applications sont similaires. En tant que telles, les listes inversées sont toujours utilisées pour implémenter d’autres structures de données, dans des piles et dans des files d’attente. Mais, il y a des utilisations uniques que les listes chaînées inverses apportent à la table:
Puisque les éléments sont inversés, nous pouvons imprimer les éléments et traiter la liste dans l’ordre inverse. Ceci est utile si vous souhaitez afficher l’historique Internet d’un navigateur. Si vous souhaitez supprimer certains éléments vers la fin de la liste, l’inverser facilite grandement la tâche. C’est parce que ces éléments sont maintenant au début de la liste. Cela peut faire gagner beaucoup de temps, surtout si la liste est importante. Vous n’avez pas besoin de parcourir toute la liste si vous inversez la liste. Parfois, nous voulons effectuer un algorithme récursif sur une liste entière, en exécutant des opérations à chaque nœud. Dans certains de ces cas, les traiter dans l’ordre inverse peut avoir plus de sens. Une autre raison d’utiliser une liste chaînée inversée est de vérifier si la liste est palindromique-cela signifie que la séquence est la même vers l’avant ou vers l’arrière. Un exemple de ceci serait le nombre 212. Quelle que soit la façon dont vous le regardez, la séquence de valeurs de données est identique.
Comment inverser une liste chaînée
Il existe généralement deux approches pour inverser une liste chaînée : l’approche itérative et l’approche récursive. Examinons-les.
L’approche itérative
Dans cette méthode, nous répétons l’exécution de l’algorithme jusqu’à ce que chaque pointeur ait été inversé. Pour ce faire, nous suivons nos nœuds à l’aide des attributs”prev”,”curr”et”next”. Nous pouvons les assigner comme tels :
while (current !=NULL) { next=current-> next current-> next=prev prev=current current=next } head_ref=prev
L’instruction”while”en gros itère sur chaque nœud qui n’est pas nul.
La ligne suivante garde une trace du nœud suivant dans la liste, afin que nous ne le perdions pas une fois que nous avons inversé les pointeurs.
Ensuite, nous définissons l’attribut”next”du nœud actuel sur le nœud précédent, en inversant les pointeurs.
La ligne suivante définit l’attribut”prev”sur le nœud précédent, en gardant une trace comme nous l’avons fait le nœud suivant.
L’avant-dernière ligne indique que le pointeur”actuel”est sur le nœud suivant, nous pouvons donc nous déplacer itérativement le long de la liste.
Enfin, nous définissons le”head_ref ” pointeur vers le dernier nœud de la liste d’origine, qui sera le premier nœud de la liste inversée. Par conséquent, nous le définissons comme le nouveau nœud principal.
Voici comment nous pouvons implémenter ce processus en Python :
nœud de classe : def __init__(self, data): self.data=data self. next=None class LinkedList : def __init__(self): self.head=None def push(self, new_data): new_node=Node(new_data) new_node.next=self.head self.head=new_node def reverse(self): prev_node=None current_node=self.head alors que current_node n’est pas None: next_node=current_node.next current_node.next=prev_node prev_node=current_node current_node=next_node self.head=prev_node def printList(self): current_node=self.head while current_node: print( current_node.data, end=””) current_node=current_node.next my_list=LinkedList() my_list.push(16) my_list.push(2) my_list.push(19) my_list.push(71) print(“Liste liée donnée”) ma_liste.printList() ma_liste.reverse () print(“\nListe chaînée inversée”) my_list.printList()
D’abord, nous définissons les classes”Node”et”LinkedList”. Ensuite, nous définissons la fonction”push”, qui sert à ajouter un nouveau nœud au début de la liste, qui est désigné comme le nœud principal.
Ensuite, nous voyons la fonction”reverse”implémentée à peu près de la même manière que décrit précédemment.
Enfin, nous définissons la fonction”printList”pour la classe”LinkedList”, qui imprime la valeur des données à chaque nœud, qui continue jusqu’à ce que le”current_node ” est égal à “Aucun”, indiquant que nous avons atteint la fin de la liste. Voir la capture d’écran pour savoir comment cela fonctionne en Python.
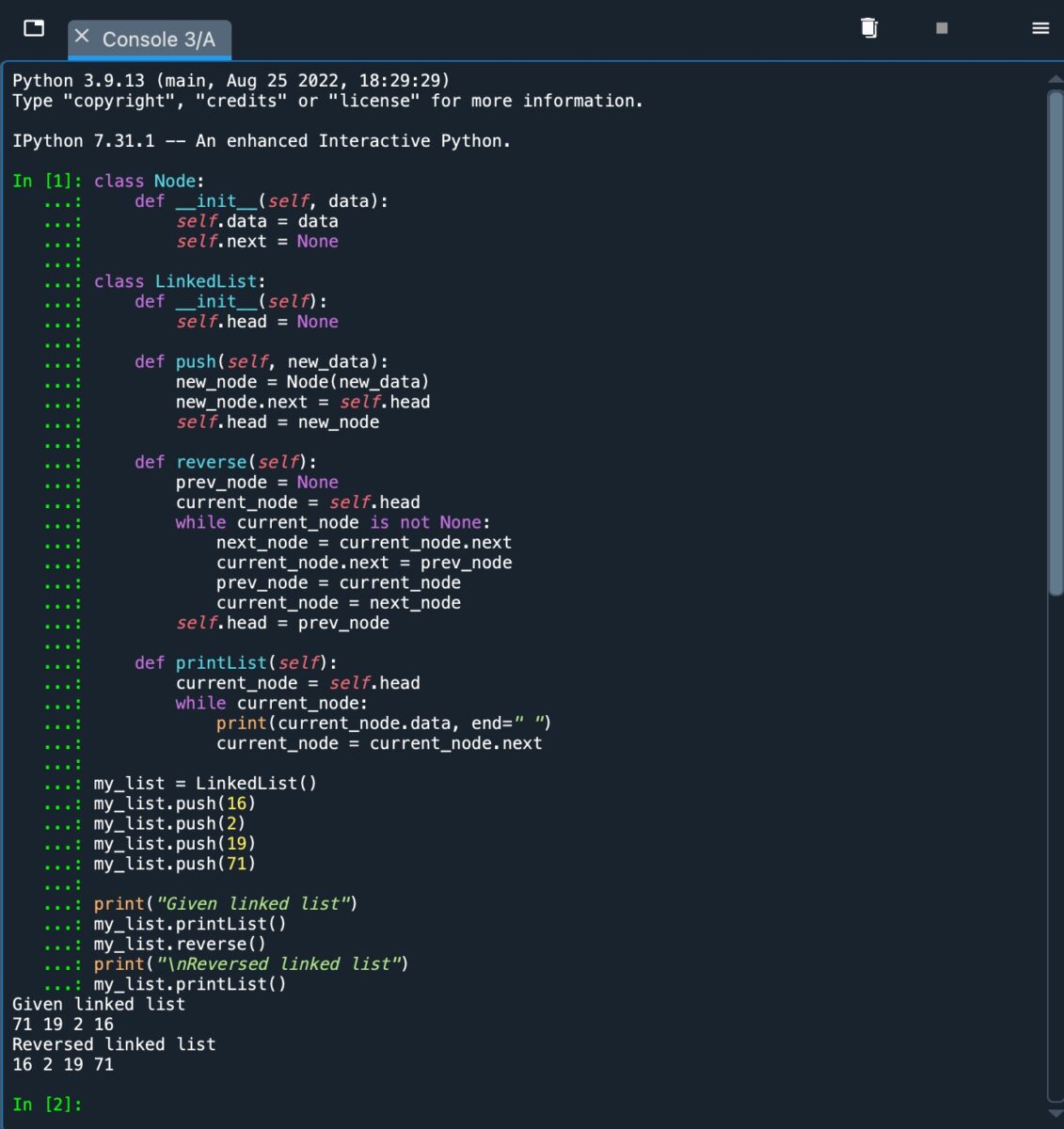 L’approche itérative pour inverser une liste chaînée, implémentée en Python.
L’approche itérative pour inverser une liste chaînée, implémentée en Python.
©”TNGD”.com
L’approche récursive
L’autre méthode d’inversion une liste chaînée est l’approche récursive. Alors que les approches itératives fonctionnent en utilisant des boucles ou des instructions répétitives pour résoudre un problème, les approches récursives exécutent la même fonction sur des exemples de plus en plus petits du même problème. Une fois ces sous-problèmes résolus, les solutions sont combinées pour donner un résultat global au problème initial. Voyons comment fonctionne la récursivité pour inverser une liste chaînée :
Tout d’abord, nous divisons la liste en deux parties, le premier nœud et la liste restante.
Ensuite, nous appelons le”reverse”pour la liste restante.
Cette liste inversée est ensuite liée au premier nœud, et le pointeur de tête d’origine est défini sur NULL. Le nouveau pointeur principal est défini sur le nouveau nœud principal et la liste est inversée.
Voici comment cela est implémenté :
nœud de classe : def__init__(self, data): self. data=data self.next=None class LinkedList : def__init__(self): self.head=None def push(self, new_data): new_node=Node(new_data) new_node.next=self.head self.head=new_node def reverse_recursive( self, current_node): si current_node est None ou current_node.next est None: return current_node rest=self.reverse_recursive(current_node.next) current_node.next.next=current_node current_node.next=None return rest def reverse(self): self. head=self.reverse_recursive(self.head) def printList(self): current_node=self.head while current_node: print(current_node.data, end=””) current_node=current_node.next print() my_list=LinkedList() my_list. push(16) ma_liste.push(2) ma_liste.push(19) ma _list.push(71) print(“Liste chaînée donnée”) my_list.printList() my_list.reverse() print(“Liste chaînée inversée (récursive) :”) my_list.printList()
Une grande partie de ce code est identique au processus itératif. La principale différence réside, sans surprise, dans la fonction inverse utilisée.
Dans ce cas, nous définissons la fonction « reverse_recursive » en fonction du nœud courant. Chaque nœud après celui-ci est inversé de manière récursive en appelant la fonction inverse avec le nœud suivant en entrée jusqu’à ce que le nœud actuel soit égal à”Aucun”. Cela se produit lorsque la fin de la liste est atteinte, ou dans le cas simple où il n’y a qu’un seul nœud dans la liste.
Ensuite, le nœud actuel est inversé en mettant à jour l’attribut « suivant » du nœud suivant au nœud courant, et l’attribut « suivant » du nœud courant à « Aucun ». Le nœud actuel devient la queue de la liste inversée.
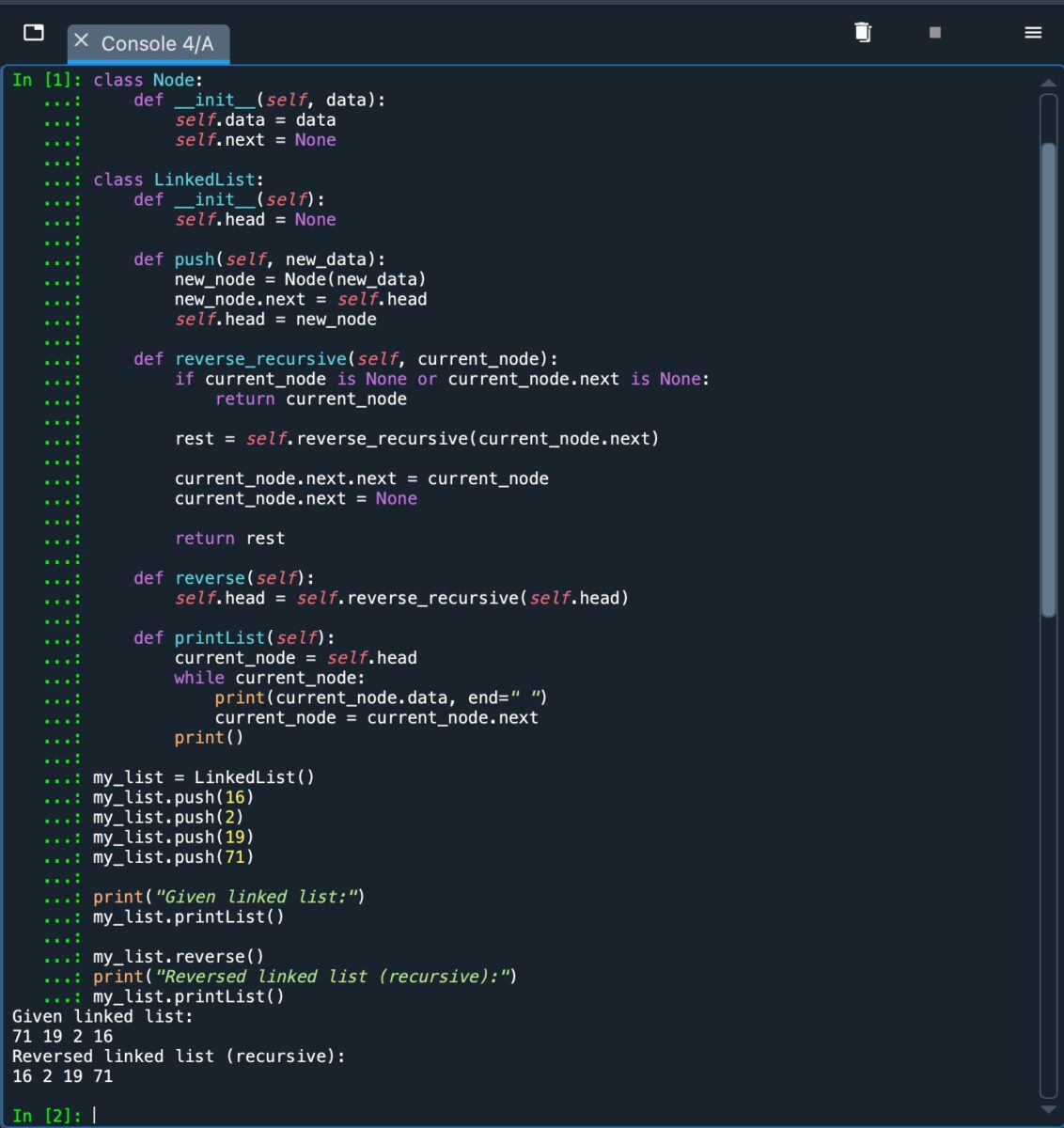 L’approche récursive pour inverser une liste chaînée, implémentée en Python.
L’approche récursive pour inverser une liste chaînée, implémentée en Python.
©”TNGD”.com
Récapitulatif
Quand vous devez inverser une liste chaînée, vous pouvez choisir entre une approche itérative et une approche récursive. Alors que les approches itératives reposent sur la répétition des mêmes instructions dans une boucle”while”pour chaque nœud, les fonctions récursives exécutent leur fonction sur des instances plus petites du même problème. Inverser une liste liée peut être utile pour détecter la palindromicité d’une liste et modifier les éléments à la fin de la liste d’origine.
Comment inverser une liste liée, avec des exemples FAQ (Foire aux questions)
Qu’est-ce qu’une liste chaînée inversée ?
Une liste chaînée inversée est une liste chaînée dont l’ordre de ses éléments est inversé, de sorte que le dernier nœud devient le premier nœud de la nouvelle liste, et les pointeurs sont inversés.
Pourquoi voudriez-vous inverser une liste liée ?
Inverser une liste peut être utile pour déterminer si une liste est palindromique, modifier les éléments à la fin de la liste d’origine (comme ils le sont maintenant au début), ou quand vous souhaitez utiliser certains algorithmes qu’il est préférable d’utiliser avec une liste inversée.
Comment pouvez-vous inverser une liste liée ?
Les moyens les plus courants d’inverser une liste liée sont les fonctions itératives ou récursives. Là où l’approche itérative fonctionne en parcourant la liste et en modifiant les pointeurs de chaque nœud, la fonction inverse récursive fonctionne en inversant la liste en dehors du nœud principal, puis en mettant à jour les pointeurs du nœud actuel.
Comment inversez-vous les listes à double lien et les listes à lien circulaire ?
Vous pouvez inverser une liste à double lien de la même manière qu’une liste à simple lien, mais vous devez mettre à jour le”suivant”et attributs”prev”de chaque nœud en conséquence. Pour les listes liées circulaires, vous devez mettre à jour l’attribut”suivant”du nœud de queue pour qu’il pointe vers le nouveau nœud principal.
Quelle est la complexité temporelle de l’inversion d’une liste liée ?
La complexité temporelle est égale à O(n), où n est le nombre de nœuds, car vous devez parcourir la liste pour inverser les pointeurs quelle que soit la méthode utilisée.
Quelle est la complexité spatiale de l’inversion d’une liste chaînée ?
La complexité spatiale est égale à O(1) en ce qui concerne l’approche itérative, puisque les variables temporaires dont vous avez besoin pour inverser la liste restent constant. Pour l’approche récursive, la complexité spatiale est égale à O(n), puisque vous devez stocker chaque appel de la fonction récursive dans une pile.