© pinkeyes/Shutterstock.com
L’algorithme de Dijkstra n’est qu’un exemple de ce que nous appelons un algorithme du plus court chemin. En un mot, ce sont des algorithmes qui sont utilisés pour trouver la distance (ou chemin) la plus courte entre les sommets d’un graphe.
Bien que le chemin le plus court puisse être défini de différentes manières, telles que le temps, le coût ou la distance, il fait généralement référence à la distance entre les nœuds. Si vous voulez en savoir plus sur le fonctionnement de l’algorithme de Dijkstra et à quoi vous pouvez l’utiliser, vous êtes au bon endroit.
Qu’est-ce que l’algorithme de Dijkstra ?
En termes simples, l’algorithme de Dijkstra est une méthode pour trouver le chemin le plus court entre les nœuds d’un graphe. Un nœud source est désigné, puis la distance entre ce nœud et tous les autres nœuds est calculée à l’aide de l’algorithme.
Contrairement à certains autres algorithmes de chemin le plus court, celui de Dijkstra ne peut fonctionner qu’avec des graphiques pondérés non négatifs. C’est-à-dire des graphiques où la valeur de chaque nœud représente une certaine quantité, telle que le coût ou la distance, et toutes les valeurs sont positives.
L’algorithme
Avant de plonger dans la façon d’implémenter l’algorithme de Dijkstra en utilisant code, passons en revue les étapes impliquées :
Tout d’abord, nous initialisons une file d’attente prioritaire vide ; appelons cela”Q”. C’est la manière la plus efficace d’utiliser l’algorithme, car il garantit que nous sélectionnons toujours le prochain sommet le plus proche du nœud source. Puisque nous ne connaissons pas encore les distances de chaque sommet au nœud source, nous initialisons toutes les distances de sommet à l’infini. La distance du sommet source, ou nœud source, est également définie sur 0 car il s’agit de notre point de départ. Le nœud source est ensuite ajouté à la file d’attente prioritaire avec une priorité de 0. Pour commencer, le sommet avec le plus petit distance est supprimée de la file d’attente. Ce sommet est appelé « u » et les sommets voisins sont désignés « v ». La distance du nœud source à chaque v à travers u est calculée, et si la distance est inférieure à la distance actuelle à v, la distance est mise à jour. Une fois que v est calculé, il est inséré dans la file d’attente prioritaire avec sa priorité définie sur équivalent à sa distance au sommet source. Cela garantit que les sommets avec des distances plus petites sont prioritaires en premier, maintenant l’efficacité de l’algorithme en considérant d’abord les sommets non visités les plus proches.
Fonctionnement de l’algorithme de Dijkstra
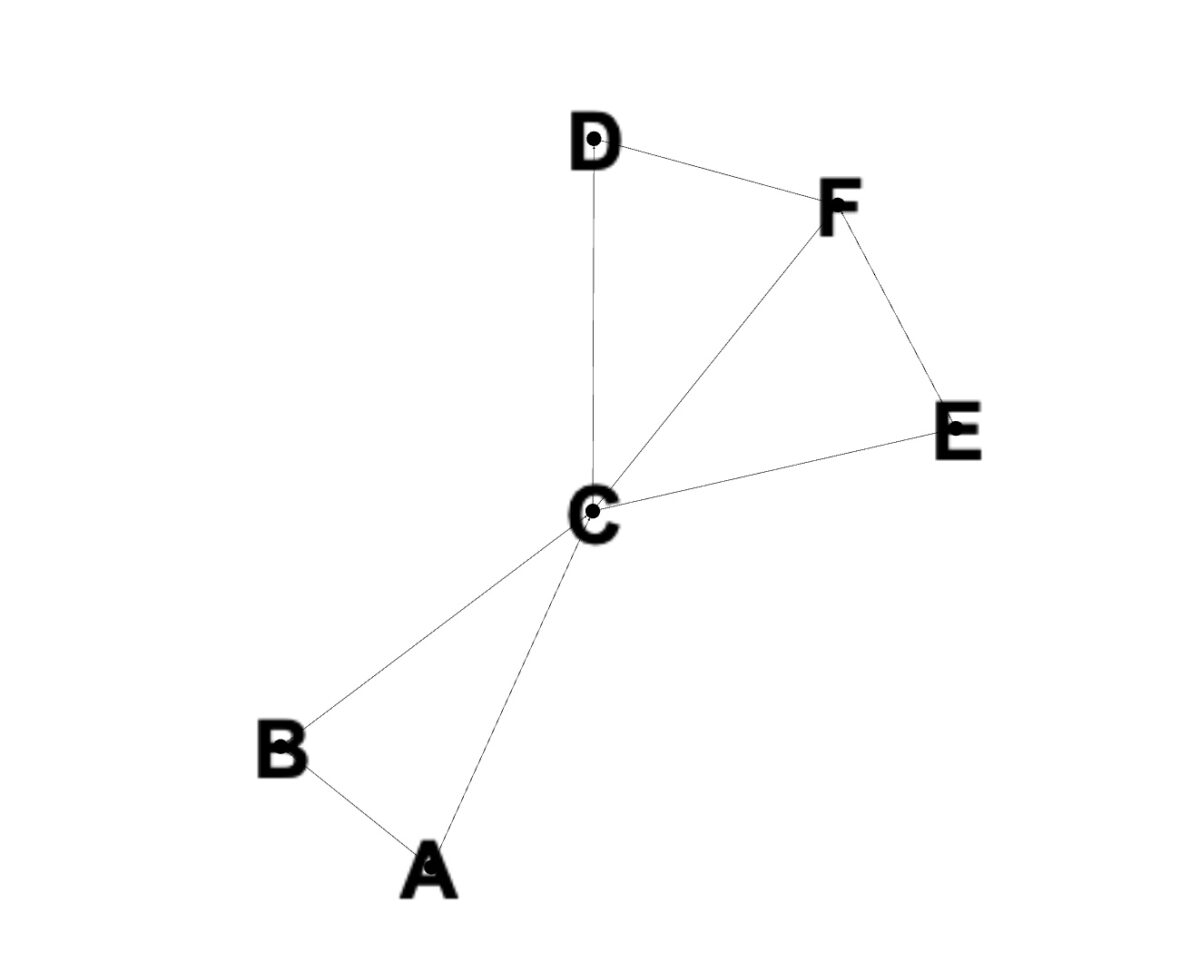Vertices A à F.
©”TNGD”.com
Maintenant que nous avons couvert les bases de l’algorithme de Dijkstra, regardons comment cela fonctionnerait avec un exemple. Prenons d’abord un graphe avec des nœuds disposés comme tels :
Nous avons des sommets A à F, qui sont connectés les uns aux autres par différents chemins. Ces connexions sont également appelées arêtes. Si nous choisissons A comme sommet de départ, toutes les valeurs de chemin pour les autres nœuds sont définies sur l’infini, comme indiqué précédemment.
Nous allons ensuite à chaque sommet et mettons à jour sa longueur de chemin. Si la distance calculée au nœud adjacent est inférieure à la distance actuelle à ce sommet, la distance est mise à jour.
Si nous définissons la priorité de chaque sommet égale à sa distance à la source, nous évitons de visiter deux fois les nœuds. Lors de la visite d’un nœud non visité, nous optons d’abord pour la longueur du chemin le plus court. Ce processus est répété jusqu’à ce que chaque nœud ait été visité et que la distance par rapport au nœud source soit calculée.
Implémentation de l’algorithme de Dijkstra à l’aide d’un tas
Il est temps d’implémenter du code pour l’algorithme de Dijkstra dans Python et voyez comment cela fonctionne. Nous allons commencer par utiliser une implémentation simple d’une file d’attente prioritaire, connue sous le nom de tas. Le code peut être représenté comme suit:
import heapq import sys def dijkstra_heap(adj_matrix, source): num_vertices=len(adj_matrix) distances=[sys.maxsize] * num_vertices distances[source]=0 visited=[False] * num_vertices heap=[(0, source)] while heap : current_distance, current_vertex=heapq.heappop(heap) visited[current_vertex]=True for neighbor_vertex in range(num_vertices) : weight=adj_matrix[current_vertex][neighbor_vertex] si non visité [neighbor_vertex] et poids !=0 : distance=current_distance + weight if distance distances[neighbor_vertex] : distances[neighbor_vertex]=distance heapq.heappush(heap, (distance, neighbor_vertex)) return distances adj_matrix=[ [0, 2, 2 , 0, 0, 0], [2, 0, 2, 0, 0, 0], [2, 2, 0, 2, 2, 6], [0, 0, 2, 0, 2, 2], [0, 0, 2, 2, 0, 2], [0, 0, 6, 2, 2, 0] ] distances=dijkstra_heap(adj_matrix, 0) print(di stances)
Explication du code
Décomposons ce code étape par étape afin que nous puissions comprendre ce qui se passe.
Importer des modules
Tout d’abord, nous importons les modules”heapq”et”sys”. Le premier module nous permet d’utiliser la structure de données du tas, tandis que le second nous permet d’utiliser la valeur entière maximale. Ceci est nécessaire car nous initialisons les distances des sommets à l’infini.
Définition de l’algorithme de Dijkstra
Ensuite, nous définissons”dijkstra_heap”comme une fonction avec deux arguments-“adj_matrix”et”source”. Il s’agit d’une représentation du graphe sous la forme d’une matrice d’adjacence et de l’index du nœud source, respectivement.
Visiter les nœuds
Dans ce bloc, nous calculons le nombre de sommets. Ensuite, nous initialisons les distances du sommet source à chaque sommet de destination à l’infini, comme mentionné précédemment. La distance du nœud source est également définie sur zéro.
Une liste est alors créée, appelée”visitée”, qui est initialisée à”Faux”. Cela signifie que les nœuds sont initialement considérés comme non visités jusqu’à ce que nous ayons calculé la distance entre eux et la source. Une file d’attente prioritaire, appelée”tas”, est également créée, avec le sommet de début et la distance depuis le nœud source désignés comme un tuple.
Mettre à jour les longueurs de chemin les plus courtes
Ensuite, nous avoir une boucle”while”qui s’exécute jusqu’à ce que la file d’attente soit vide. La première ligne prend le sommet du tas qui a la distance la plus courte du sommet source, et la deuxième ligne marque le sommet comme visité une fois cette distance calculée.
Nous suivons cela avec une boucle”for”, qui itère sur tous les voisins du sommet qui nous intéresse actuellement. Le poids de chaque arête est récupéré, et si les nœuds voisins ont été visités est vérifié ainsi que si les poids sont non nuls. La distance au nœud voisin est ensuite calculée en utilisant la distance entre la source et le nœud actuel.
Nous avons une autre instruction”if”, qui vérifie si la distance calculée est plus courte que la distance la plus courte actuelle dans notre liste”distances”. Si tel est le cas, la ligne suivante met à jour cette valeur. Enfin, le sommet voisin, ainsi que sa distance par rapport à la source, est ajouté au tas.
Sortie des résultats
Une fois ce processus terminé, les distances entre le nœud source et tous les autres nœuds du graphique sont renvoyés à la console.
L’avant-dernier bloc de code représente simplement le graphique que nous examinons sous la forme d’une matrice de contiguïté, où la valeur dans la cellule {i, j} représente le poids de l’arête qui relie les deux sommets.
Le code final indique simplement au système de calculer les distances de chemin les plus courtes, puis de les imprimer sur la console.
Implémentation du code
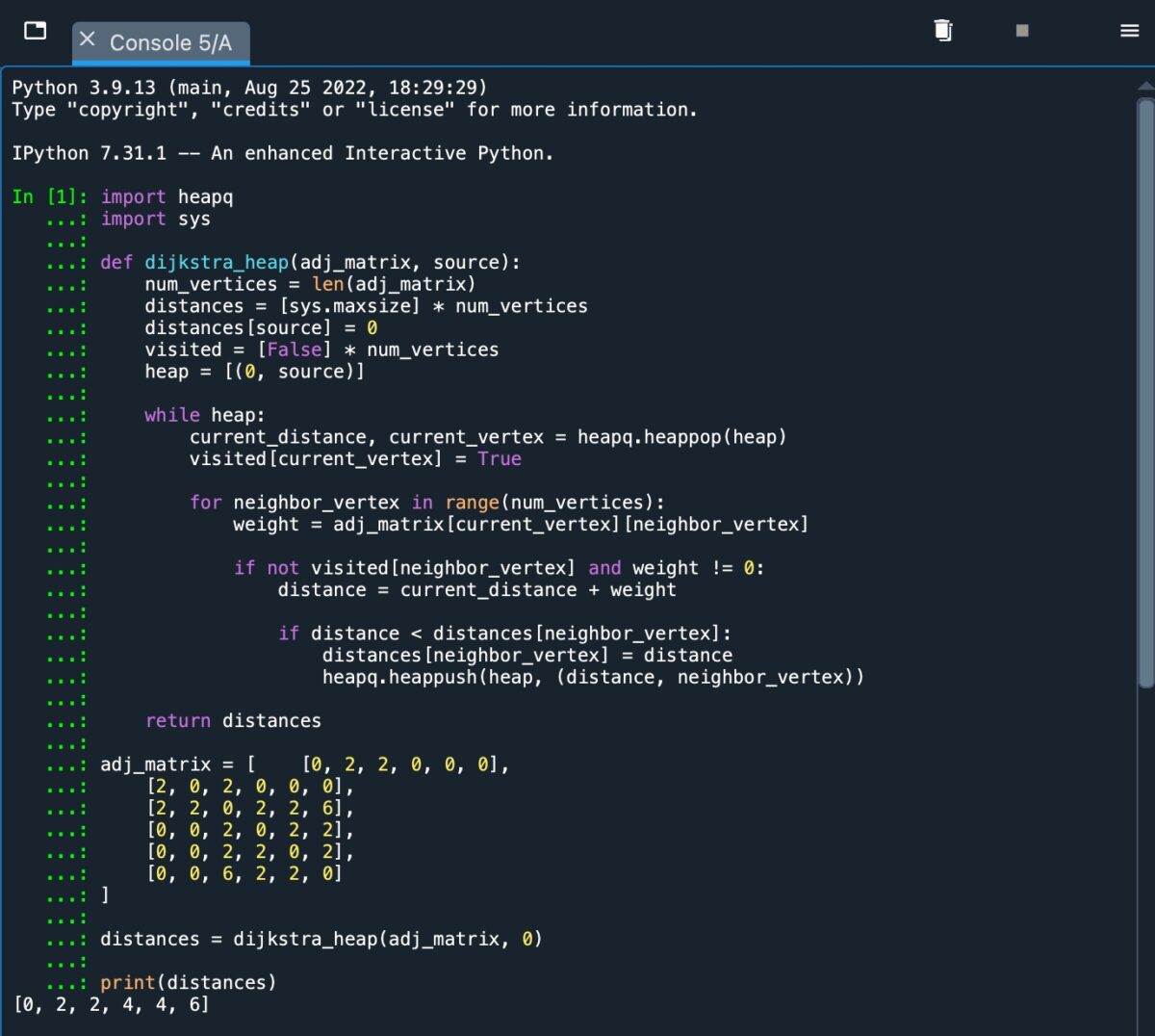La simple implémentation d’un heap.
©”TNGD”.com
Comme nous pouvons le voir sur la capture d’écran, nous recevons une sortie de [0, 2, 2, 4, 4, 6], représentant la distance du chemin le plus court du nœud source A aux nœuds B, C, D, E et F.
Meilleure et pire utilisation Cas de l’algorithme de Dijkstra
D’une manière générale, l’algorithme de Dijkstra est considéré comme efficace, bien que certains algorithmes puissent mieux fonctionner dans des cas spécialisés. Cela dit, examinons la complexité temporelle et spatiale de l’algorithme de Dijkstra dans le meilleur cas, la moyenne et le pire des cas.
Complexité temporelle de l’algorithme de Dijkstra
Habituellement, nous n’avons qu’une seule complexité pour chaque cas. Mais, avec l’algorithme de Dijkstra, la situation n’est pas aussi claire. En effet, vous pouvez implémenter l’algorithme de différentes manières, principalement en utilisant une file d’attente prioritaire.
Lorsque vous utilisez une file d’attente prioritaire, vous pouvez utiliser soit une méthode de tas binaire, soit une méthode de tas de Fibonacci. Généralement, le tas de Fibonacci conduit à des performances plus efficaces et à une meilleure complexité temporelle dans le pire des cas de O ((E + V) log V), où E est le nombre d’arêtes et V est le nombre de sommets.
Si vous n’utilisez pas de file d’attente prioritaire et que le graphe est dense, la complexité dans le pire des cas pourrait être aussi inefficace que O(V2 log V).
En ce qui concerne le cas moyen , la complexité temporelle est un peu plus favorable. Le cas moyen fait référence à l’utilisation d’une file d’attente prioritaire pour calculer les distances minimales jusqu’à chaque sommet.
Le meilleur cas, à proprement parler, est inhabituel. Vous ne prendriez probablement pas la peine d’utiliser l’algorithme pour le résoudre. En effet, le meilleur des cas serait que le sommet source soit le même que le sommet de destination. Cela signifie que l’itération se termine après une seule boucle.
La complexité est en fait identique au cas moyen. Mais comme les valeurs de E et V sont égales à 1, cela est simplifié en O(1). Si vous utilisez un tas pour implémenter votre algorithme, la complexité dans le meilleur des cas passe à O(E* log V). C’est parce qu’il y aura un maximum de sommets O(E) dans votre file d’attente.
Complexité spatiale de l’algorithme de Dijkstra
Comme pour la complexité temporelle, la complexité spatiale de l’algorithme dépend de votre implémentation. Si vous utilisez une liste de contiguïté pour représenter votre graphique et un tas de Fibonacci ou un tas régulier, la complexité est égale à O(V+E). En effet, la distance des sommets à la source, ainsi que les arêtes entre les sommets, doivent être stockées en mémoire.
Cependant, si vous utilisez une matrice d’adjacence à la place, la complexité est réduite à O( V2). En effet, vous devez stocker les distances des sommets ainsi qu’une matrice V * V pour représenter les arêtes.
Récapitulation
Pour résumer, l’algorithme de Dijkstra est l’un des nombreux algorithmes utilisés pour calculer les longueurs de chemin les plus courtes dans un graphique et est très utile. Bien qu’il existe de nombreuses façons d’implémenter l’algorithme, l’utilisation d’une file d’attente prioritaire d’une certaine description est généralement votre meilleur pari.
Parmi ces méthodes, l’utilisation d’un tas de Fibonacci tend à être la plus efficace, en particulier pour les grands graphes. Pour les graphiques plus petits, cependant, une file d’attente prioritaire plus simple peut être plus que suffisante.
Suivant
L’algorithme du plus court chemin de Dijkstra expliqué, avec des exemples FAQ (Foire aux questions)
Qu’est-ce que l’algorithme de Dijkstra ?
L’algorithme est utilisé pour calculer les longueurs de chemin les plus courtes entre les nœuds d’un graphique. Il s’agit d’une méthode itérative qui commence par la distance la plus courte du nœud source, puis met à jour la distance aux nœuds voisins au fur et à mesure.
Quelles sont les limites de l’algorithme de Dijkstra ?
L’algorithme ne peut pas gérer les fronts de poids négatifs, ce qui entraînera des résultats incorrects.
Quelle est la complexité temporelle de l’algorithme de Dijkstra ?
La complexité temporelle dépend si vous utilisez une file d’attente prioritaire et comment vous l’implémentez. Dans le meilleur des cas, où une seule itération est nécessaire, la complexité est O(1).
Sinon, le meilleur des cas est soit O(E* log V) soit O(E + V log V) , selon que vous utilisez un tas standard ou un tas de Fibonacci.
Dans les deux cas, les complexités pour les cas moyens et les pires sont les mêmes. Le pire des cas peut être équivalent à O(V2 log V) si vous n’utilisez pas du tout de file d’attente prioritaire.
Quelle est la complexité spatiale de l’algorithme de Dijkstra ?
Cela dépend de l’implémentation mais peut aller de O(V2) à O(V + E).
Pouvez-vous utiliser l’algorithme de Dijkstra sur un graphe qui a des cycles ?
Oui, tant qu’aucune des arêtes de poids n’est négative.
Quelles sont les différentes manières d’implémenter l’algorithme de Dijkstra ?
Vous pouvez utiliser une file d’attente prioritaire, telle qu’un tas ou un tas de Fibonacci. Généralement, un tas de Fibonacci conduit à des résultats plus efficaces avec des graphiques plus grands.
Quelles sont les alternatives à l’algorithme de Dijkstra ?
D’autres algorithmes de chemin le plus court incluent le A * algorithme, algorithme de Bellman-Ford et algorithme de Floyd-Warshall. A* a tendance à être plus rapide mais nécessite plus de mémoire.
Bellman-Ford et Floyd-Warshall peuvent tous deux gérer des fronts de poids négatifs contrairement à Dijkstra, mais les deux sont plus inefficaces que Dijkstra-ils ont des complexités temporelles de O(VE ) et O(V3) respectivement.