© BEST-BACKGROUNDS/Shutterstock.com
Lorsqu’il s’agit de trier un tableau de données, il existe de nombreux algorithmes de tri que vous pouvez utiliser. L’un des algorithmes les plus faciles à utiliser est le tri par insertion, en raison de sa relative simplicité et de sa nature intuitive. Lisez la suite pour découvrir exactement ce qu’est le tri par insertion, comment il est implémenté et à quoi il peut servir, avec un exemple.
Qu’est-ce que le tri par insertion ?
Le tri par insertion est un tri algorithm, l’une des méthodes que vous pouvez utiliser pour trier un tableau. La façon dont cela fonctionne n’est pas trop compliquée à comprendre et peut être largement comparée à la façon dont vous triez un jeu de cartes.
Dans Dans ce cas, nous commencerions par supposer que la première carte du jeu est déjà triée. Ensuite, nous sélectionnons une carte non triée et la trions. Cela se fait en le comparant à la première carte. Si la carte sélectionnée est supérieure à la carte triée, elle est placée à droite de la première carte. Si la carte en question est inférieure à la carte triée, elle est placée dans une position à gauche.
Ce processus se poursuit jusqu’à ce que toutes les cartes non triées soient placées dans leurs positions correctes. Le tri par insertion fonctionne de manière très similaire. Chaque valeur de données non triée est triée selon le même type de processus itératif.
Étant donné que le tri par insertion est un algorithme assez simple, il est préférable de l’utiliser pour des ensembles de données relativement petits, ainsi que pour ceux qui sont déjà quelque peu triés. De cette façon, il est connu comme un algorithme adaptatif et efficace. Ensuite, nous passerons en revue la théorie du fonctionnement du tri par insertion.
L’algorithme derrière le tri par insertion
La méthode de tri par insertion peut être représentée de manière concise avec le pseudocode suivant :
insertionSort(array) marque le premier élément comme trié pour chaque élément non trié X’extrait’l’élément X pour j-lastSortedIndex jusqu’à 0 si l’élément actuel j > X déplace l’élément trié vers la droite d’une boucle de rupture et insère X ici end insertionSort
En termes simples, cela signifie que le premier élément est supposé être trié. Chaque élément suivant est comparé au premier élément. S’il est plus petit que l’élément trié, il est déplacé vers la première ou la 0e position. S’il est supérieur, il est déplacé d’une position vers la droite. Les itérations continuent jusqu’à ce que tous les éléments aient été triés.
Le fonctionnement interne du tri par insertion
Maintenant que nous avons couvert le fonctionnement du tri par insertion et la théorie qui le sous-tend, il est temps d’illustrer le processus avec un tableau adapté. Si nous considérons l’ensemble de données suivant :
Nous pouvons supposer que le premier élément, 10, est déjà trié. Après cela, nous prenons le deuxième élément, 14, et le stockons séparément. En comparant 14 à 10, nous pouvons voir qu’il est plus grand, il conserve donc sa position de deuxième élément. Il s’agit de la première itération, appelée première passe. Le premier élément, 10, est stocké dans un sous-tableau.
Où vert=tableau trié
Pour la deuxième passe, nous passons au troisième élément, qui est 5. C’est par rapport aux éléments précédents. Nous pouvons dire qu’il est plus petit que l’élément précédent, 14, donc il échange sa place avec 14.
L’algorithme le compare ensuite aux éléments du sous-tableau trié. 5 est également inférieur à 10, il est donc déplacé au début du sous-tableau. Le tableau trié a maintenant 2 éléments-5 et 10.
Maintenant, nous passons à la troisième passe. Dans ce cas, 7 est l’élément sélectionné. C’est plus petit que 14, il est donc déplacé d’une position vers la gauche et dans le tableau trié. Ce n’est pas la bonne position, car 7 est plus petit que 10 mais plus grand que 5. Par conséquent, il est déplacé d’une autre position vers la gauche.
Pour la quatrième passe, nous regardons la quatrième élément, qui est 14. Ceci est déjà trié, donc maintenant le tableau trié comprend 5, 7, 10 et 14.
Le résultat final
Enfin, pour la cinquième passe, nous prenons le cinquième élément, qui est 1. C’est clairement plus petit que 14, donc la position est permutée. Il est également inférieur à 10, donc la position est à nouveau échangée. Cela continue deux fois de plus, car 1 est le plus petit élément du tableau. Par conséquent, nous nous retrouvons avec un tableau trié comme suit :
L’implémentation du tri par insertion
Le tri par insertion peut être implémenté avec une variété de langages de programmation, de C, C# et C++ à Java, Python, PHP et Javascript. À des fins d’illustration, nous allons travailler avec Python. L’ensemble du processus peut être représenté dans le code suivant :
def insertionSort(arr): if (n:=len(arr))=1 : return for i in range(1, n): key=arr[i ] j=i-1 tant que j >=0 et clé arr[j]: arr[j+1]=arr[j] j-=1 arr[j+1]=clé arr=[10, 14, 5, 7, 1] insertionSort(arr) print(arr)
Tout d’abord, nous définissons le tri par insertion en fonction du tableau, (arr). Ensuite, nous disons que, si le tableau est de longueur 1 ou moins, le tableau est renvoyé. Ensuite, nous définissons l’élément à la ième position d’un tableau de longueur n comme clé.
Nous mettons des contraintes sur le calcul afin que j ne soit utilisé que lorsqu’il est supérieur ou égal à l’indice 0. J est considéré comme la valeur à gauche de l’élément que nous examinons, comme par j=je-1. Si sa valeur est supérieure à la clé, sa position est décalée vers la droite.
La dernière ligne, arr[j+1]=clé, dicte que la valeur à droite de cette valeur j devient la nouvelle clé. Par conséquent, le reste des nombres est permuté si nécessaire. Ce processus se poursuit ensuite depuis le début, jusqu’à ce que tous les nombres soient correctement triés.
Tri par insertion en Python : implémentation
Voyons comment cela est implémenté en Python dans l’environnement Spyder. Nous utiliserons le même tableau que précédemment pour illustrer cela clairement. Voir le code implémenté ci-dessous :
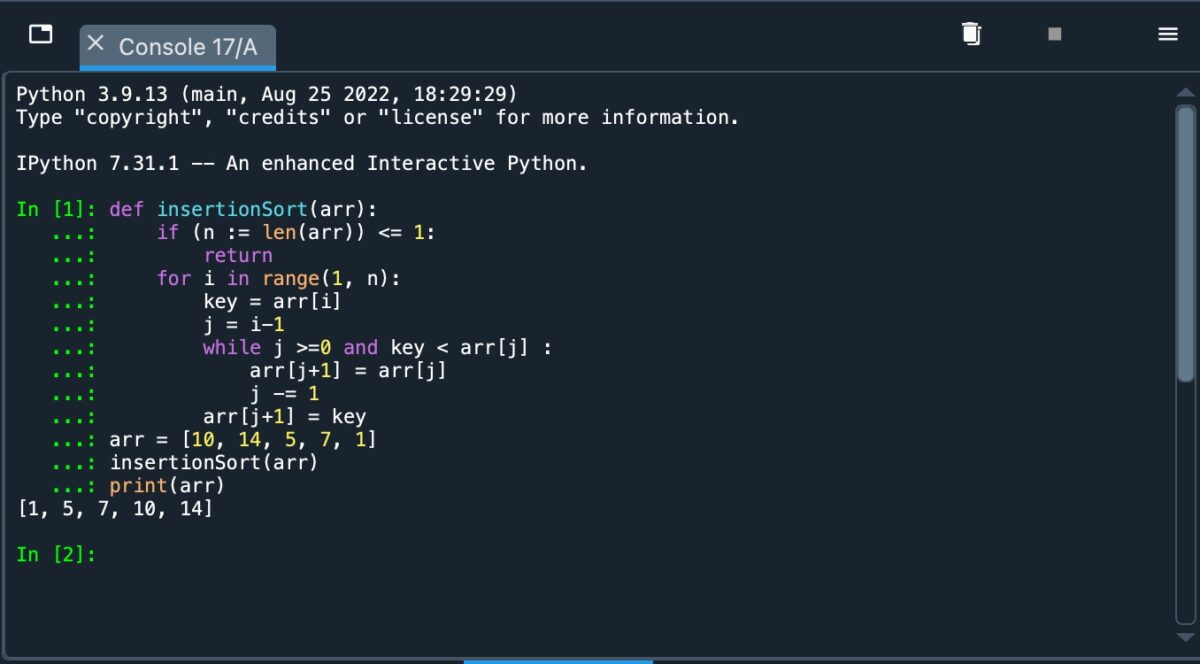Mise en œuvre du tri par insertion dans Python.
©”TNGD”.com
Un élément clé à retenir est que l’indentation est essentielle lors de l’utilisation de Python. Si l’indentation n’est pas utilisée correctement, vous recevrez un message d’erreur qui ressemble à quelque chose ci-dessous.
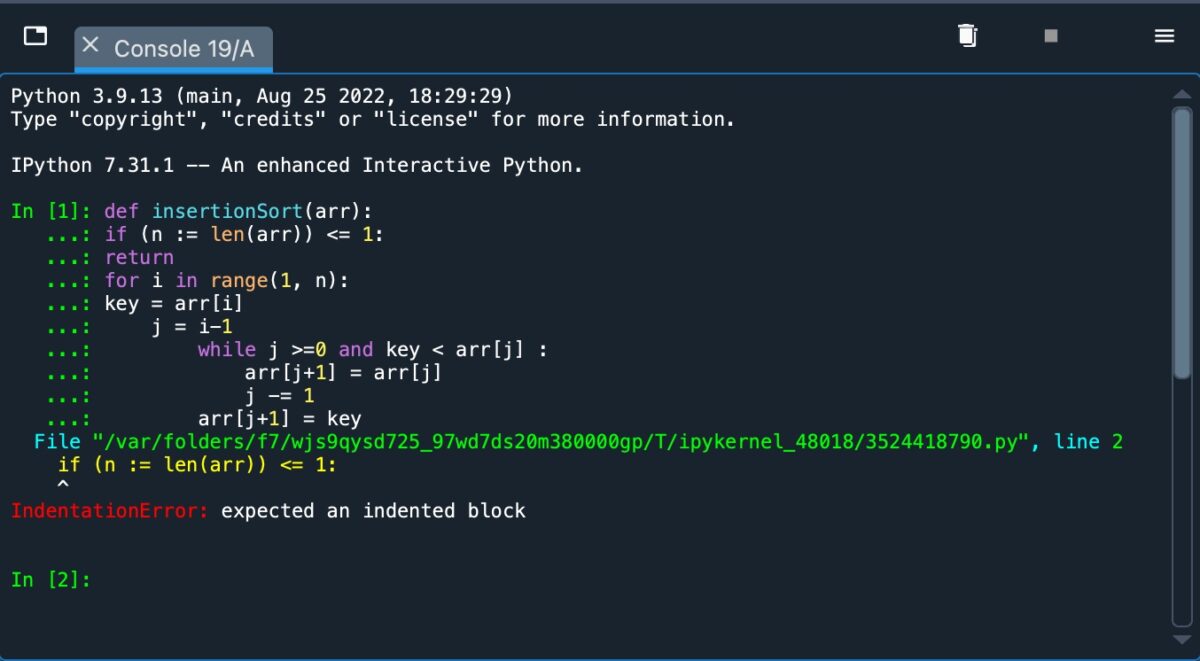Réception d’un message d’erreur.
©”TNGD”.com
Meilleurs et pires cas d’utilisation du tri par insertion
Bien que le tri par insertion soit utile à de nombreuses fins, comme avec tout algorithme, il a ses meilleurs et ses pires cas. Ceci est principalement dû à la complexité temporelle et spatiale.
Complexité temporelle avec le tri par insertion
La complexité temporelle dans chaque cas peut être décrite dans le tableau suivant :
Vous pouvez voir que, dans le meilleur des cas, la complexité temporelle est égale à O(n). Cela signifie qu’aucun tri n’est requis, car le tableau est déjà trié. Étant donné que l’algorithme doit vérifier chaque valeur dans l’ordre avant de pouvoir déterminer que le tableau est trié, la complexité temporelle est linéaire. Autrement dit, la complexité est linéairement proportionnelle à la taille de l’entrée.
Dans les cas moyens et les pires, cependant, la complexité est égale à O(n2). Un cas moyen serait celui où les éléments du tableau sont mélangés, ni ascendants ni descendants. Dans le pire des cas, les éléments devraient être triés à l’envers.
C’est parce qu’ils sont déjà dans l’ordre croissant ou décroissant et que vous avez besoin de l’ordre inverse. Ce type de complexité est appelé temps quadratique car il dépend de n2. Par exemple, si la taille de l’entrée est de 4, le nombre d’opérations serait de 16.
Complexité spatiale avec tri par insertion
L’autre type de complexité est la complexité spatiale. Il s’agit de la quantité d’espace mémoire nécessaire pour exécuter l’algorithme. Une complexité de O(1) signifie que la quantité de mémoire requise est constante, quelle que soit la taille de l’entrée.
Ceci est vrai dans le cas du tri par insertion car vous n’utilisez qu’une seule variable temporaire à chaque opération. En d’autres termes, une seule valeur est triée à la fois, donc l’utilisation de la mémoire est constante.
Il convient de noter que le tri par insertion est considéré comme un algorithme stable, ce qui signifie que l’ordre relatif des éléments avec des valeurs égales est conservé. Ceci est utile si vous devez conserver l’ordre d’éléments spécifiques ou trier des tableaux déjà partiellement triés. En effet, les éléments ne sont pas échangés avec la clé s’ils lui sont équivalents.
Récapitulatif
Nous avons expliqué ce qu’est le tri par insertion et quand il convient de l’utiliser. En plus de cela, nous avons pris en compte sa complexité temporelle et spatiale et montré sa représentation de code et son implémentation en Python. Si vous cherchez à trier un tableau relativement petit, en particulier un tableau dans lequel certains éléments sont déjà triés, le tri par insertion est l’une des meilleures méthodes à utiliser.
Suivant
Qu’est-ce que c’est Le tri par insertion et comment ça marche ? (Avec exemples) FAQ (Foire aux questions)
Qu’est-ce que le tri par insertion ?
Le tri par insertion est un algorithme qui peut être utilisé pour trier des ensembles de données dans ordre croissant ou décroissant. C’est similaire à la façon dont vous triez un jeu de cartes entre vos mains, en ce sens que le premier élément est considéré comme trié.
Chaque élément suivant est ensuite comparé au premier élément et placé dans la position correcte, soit en le laissant où il se trouve, soit en le déplaçant d’une position vers la droite. Cette opération est répétée pour chaque élément, puis le processus se poursuit depuis le début jusqu’à ce que tous les éléments soient triés.
Quand devez-vous utiliser le tri par insertion ?
Le tri par insertion est mieux utilisé pour les petits ensembles de données et ceux où les valeurs sont déjà partiellement triées.
Quels langages de programmation peuvent implémenter le tri par insertion ?
Beaucoup des langages de programmation peuvent implémenter le tri par insertion, y compris C, C++, C#, Java, Javascript, PHP et Python.
Quels sont les avantages du tri par insertion ?
Les avantages du tri par insertion sont qu’il est simple, que l’ordre relatif des clés ne change pas, qu’il est efficace pour les petits ensembles de données et qu’il peut trier une liste pendant sa réception.
Comment le tri par insertion est-il optimisé ?
Le tri par insertion est optimisé en créant un sous-tableau stocké, où les valeurs triées sont temporairement stockées. Cela signifie qu’un échange complet des éléments du tableau à chaque itération n’est pas nécessaire, car les éléments sont échangés un par un.
Combien d’itérations y a-t-il dans le tri par insertion ?
Avec un tableau de longueur n, il faut n-1 itérations pour trier l’intégralité du tableau.
Comment modifier le tri par insertion ?
Le tri par insertion peut être modifié en utilisant le tri par insertion binaire. Ceci est similaire au tri par insertion en ce sens qu’il s’agit d’un algorithme stable, mais il réduit le nombre de comparaisons à effectuer.
La complexité temporelle est réduite de O(n) à O(log n) car il utilise la recherche binaire plutôt que la recherche linéaire. Chaque valeur est comparée aux valeurs du sous-tableau trié pour déterminer quelle valeur est juste supérieure à la valeur sélectionnée. Cela réduit le nombre d’opérations.
Quels sont les inconvénients du tri par insertion ?
Le tri par insertion n’est pas approprié pour les ensembles de données particulièrement volumineux, car le la complexité temporelle dans la moyenne et le pire des cas est quadratique.
Quelles sont les alternatives au tri par insertion ?
Avec des ensembles de données volumineux et confus, des alternatives plus appropriées sont le tri rapide, le tri par fusion ou le tri par tas.
Le tri par insertion est-il un algorithme stable ?
Oui, le tri par insertion est considéré comme un algorithme de tri stable, car les éléments restent inchangés s’ils sont égaux à la clé. L’ordre des éléments est également préservé s’ils sont équivalents les uns aux autres.