De nombreux algorithmes de tri peuvent être utilisés pour trier des ensembles de données. Généralement, ces données sont présentées dans une liste ou un tableau. Parmi ces algorithmes, l’algorithme de tri par sélection est l’un des plus simples à comprendre et à mettre en œuvre. Dans cet article, nous allons expliquer la théorie du tri par sélection, son implémentation et les meilleures pratiques d’utilisation de l’algorithme.
Qu’est-ce que le tri par sélection ?
Le tri par sélection est un algorithme de tri basé sur la comparaison. Cela fonctionne en divisant le tableau en deux parties-triées et non triées. L’élément avec la plus petite valeur est sélectionné et placé à l’index 0 du sous-tableau trié. Le plus grand élément peut également être sélectionné en premier, selon que vous souhaitez que votre liste soit dans l’ordre croissant ou décroissant. Il s’agit d’un processus itératif, ce qui signifie que la méthode est répétée jusqu’à ce que tous les éléments soient placés dans le tableau trié dans leurs positions correctes. Comme vous pouvez vous y attendre, à chaque itération, la taille du sous-tableau trié augmente d’un élément, tandis que la taille du tableau non trié diminue d’un élément.
 Vous pouvez implémenter le tri par sélection avec une variété de langages de programmation, y compris C, C++, C#, PHP, Java, Javascript et Python.
Vous pouvez implémenter le tri par sélection avec une variété de langages de programmation, y compris C, C++, C#, PHP, Java, Javascript et Python.
L’algorithme derrière le tri par sélection
L’algorithme derrière le tri par sélection est assez simple et suit ces étapes :
 L’élément minimum dans le tableau non trié est trouvé et échangé avec le premier élément, dans l’index 0. Le tableau non trié est alors traversé pour trouver le nouvel élément minimum.Si un élément est plus petit que l’élément de l’index 0, les éléments sont permutés.L’élément minimum suivant dans le tableau non trié est trouvé et ajouté au sous-tableau trié, en suivant la contrainte précédente.Ce processus est répété jusqu’à ce que le tableau entier soit trié.
L’élément minimum dans le tableau non trié est trouvé et échangé avec le premier élément, dans l’index 0. Le tableau non trié est alors traversé pour trouver le nouvel élément minimum.Si un élément est plus petit que l’élément de l’index 0, les éléments sont permutés.L’élément minimum suivant dans le tableau non trié est trouvé et ajouté au sous-tableau trié, en suivant la contrainte précédente.Ce processus est répété jusqu’à ce que le tableau entier soit trié.
Fonctionnement du tri par sélection
Maintenant que nous avons couvert le fonctionnement du tri par sélection, il est temps d’illustrer cela avec un exemple.
Si nous considérons le tableau [72, 61, 59, 47, 21] :
La première passe, ou itération, du processus implique de parcourir le tableau entier de l’index 0 à l’index 4 (rappelez-vous que le premier index est défini sur 0, et non sur 1).
L’élément minimum trouvé est 21, il est donc remplacé par le premier élément, 72. Ceci est illustré ci-dessous.
[21, 61, 59, 47, 72]
où vert=élément trié
Pour la deuxième passe, nous trouvons que 47 est la deuxième plus petite valeur. Ceci est ensuite échangé avec 61.
[21, 47, 59, 61, 72]
La troisième passe détecte 59 comme étant le troisième élément, qui est déjà en position. Par conséquent, aucun échange ne se produit.
[21, 47, 59, 61, 72]
La quatrième passe trouve que 61 est le quatrième élément qui, encore une fois, est déjà en place.
[21, 47, 59, 61, 72]
La cinquième et dernière passe donne à peu près la même chose. 72 est le cinquième plus petit, ou le plus grand élément, et est dans la bonne position. Maintenant, le tableau est complètement trié par ordre croissant.
[21, 47, 59, 61, 72]
Implémentation du tri par sélection
Nous pouvons implémenter tri par sélection avec une variété de langages de programmation, y compris les plus courants-C, C++, C#, PHP, Java, Javascript et Python. Pour illustration, nous allons utiliser Python. Le code utilisé avec Python est le suivant:
def SSort(arr, size): for step in range(size): min_idx=step for i in range(step + 1, size): if arr[i] arr [min_idx] : min_idx=i (arr[step], arr[min_idx])=(arr[min_idx], arr[step]) données=[-7, 39, 0, 14, 7] taille=len(données) SSort(data, size) print(‘Ascending Sorted Array:’) print(data)
Explication du code
A ce stade, une explication du code utilisé sera utile. Tout d’abord, nous définissons la fonction”SSort”comme une fonction d’un tableau avec une taille spécifiée.
La boucle”for”dicte qu’une boucle va commencer qui itérera sur une plage de”taille”, ce qui signifie la longueur du tableau. La variable « step » indique que chaque itération prendra les valeurs 0, 1, 2… jusqu’à la taille-1.
La ligne suivante montre que la valeur initiale de « step » est égale à la variable « min_idx ». C’est un moyen de garder une trace de la position de l’élément minimum dans le tableau non trié.
La boucle”for”suivante spécifie une boucle qui itérera sur le tableau non trié, en commençant à”step + 1″. C’est parce que l’élément”step”est déjà placé dans le tableau trié. La variable”i”dans chaque itération sera équivalente à step + 1, step + 2 et ainsi de suite jusqu’à la taille-1.
L’instruction”if”qui vérifie si l’élément actuel à”i”est inférieur à l’élément minimum actuel. Si tel est le cas, l’élément minimum est mis à jour pour refléter cela.
Enfin, cette ligne plutôt compliquée a une signification simple. Une fois la boucle précédente terminée, l’élément minimum non trié est échangé avec le premier élément du tableau non trié. Cela ajoute effectivement l’élément à la fin du tableau trié.
Le code en bas dicte simplement le tableau avec lequel nous travaillons, de longueur”taille”, et appelle le tri par sélection pour travailler sur ce déployer. La sortie est ensuite imprimée avec le titre”Ascending Sorted Array”.
Chaque fois que vous utilisez Python, il est essentiel que vous utilisiez la bonne indentation pour désigner les opérations distinctes. Sinon, vous recevrez un message d’erreur et le calcul ne s’exécutera pas.
A quoi ressemble le code
Consultez la capture d’écran ci-dessous pour voir à quoi ressemble ce code lorsqu’il est implémenté dans Python.
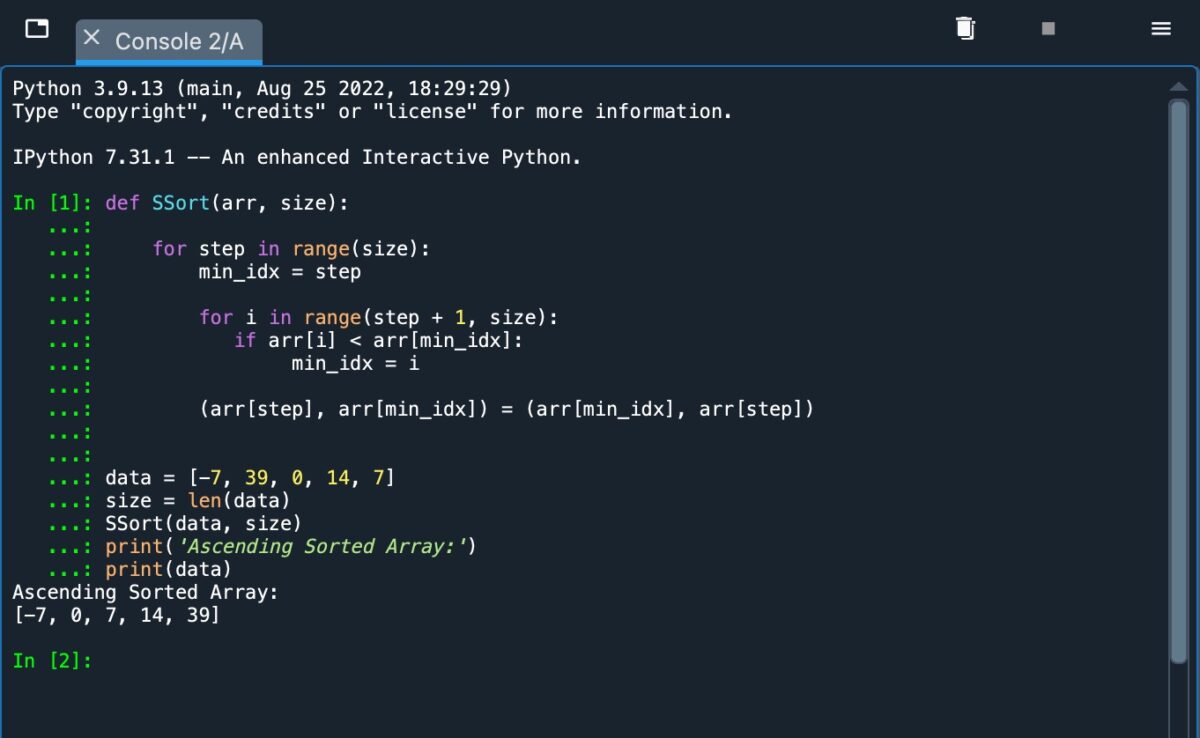 Lors de l’utilisation Python, vous devez utiliser l’indentation correcte pour désigner les opérations distinctes.
Lors de l’utilisation Python, vous devez utiliser l’indentation correcte pour désigner les opérations distinctes.
©”TNGD”.com
Les meilleurs et les pires cas d’utilisation du tri par insertion
Bien que le tri par insertion soit utile à de nombreuses fins, comme pour tout algorithme, il a ses meilleurs et ses pires cas. Cela est principalement dû à la complexité temporelle et spatiale.
Complexité temporelle avec le tri par insertion
La complexité temporelle dans chaque cas peut être décrite dans le tableau suivant :
Comme avec n’importe quel algorithme, le tri par sélection a sa propre complexité temporelle et spatiale. Cela fait essentiellement référence à la façon dont la complexité, ou la vitesse d’exécution, change dans une variété de cas. La complexité temporelle peut être résumée comme dans le tableau suivant :
Le meilleur cas fait référence au moment où le tableau est trié, le cas moyen fait référence au moment où le tableau est confus, et le pire des cas fait référence au moment où le tableau est dans l’ordre croissant ou décroissant et que vous souhaitez l’ordre opposé. En d’autres termes, ils se réfèrent au nombre d’itérations nécessaires pour terminer le processus, le pire des cas nécessitant le nombre maximum d’itérations.
Dans ce cas, la complexité temporelle est identique pour le tri par sélection dans chaque cas. En effet, l’algorithme effectue toujours le même nombre de comparaisons et d’échanges, quel que soit le tri du tableau. Par conséquent, la complexité est O(n2), également appelée temps quadratique. C’est l’une des principales raisons pour lesquelles l’algorithme n’est pas très efficace en ce qui concerne les algorithmes de tri, mais cela signifie également que l’efficacité ne dépend pas de la distribution de l’entrée.
Complexité de l’espace avec le tri par sélection
La complexité de l’espace fait référence à la quantité de mémoire nécessaire pour les calculs. Dans le cas du tri par sélection, celui-ci est égal à O(1). Cela signifie qu’une quantité constante de mémoire est requise, indépendamment de la taille de l’entrée. La seule variable temporaire stockée est”min_idx”, qui ne change pas avec l’augmentation de la taille de l’entrée.
Récapitulation
Le tri par sélection est un algorithme relativement simple mais assez inefficace pour trier les éléments dans une entrée donnée. Il convient principalement aux très petits ensembles de données et peut être implémenté avec une variété de langages de programmation. Le tri par sélection fonctionne en divisant le tableau en deux sous-tableaux, triés et non triés. Le processus parcourt ensuite un tableau pour trouver l’élément minimum et déplace cet élément vers l’index 0. Le processus est répété, trouvant les deuxième et troisième plus petits éléments et ainsi de suite et les permutant dans leurs positions d’index correctes. Cela continue jusqu’à ce que l’ensemble du tableau soit trié.
Suivant…
Explication de l’algorithme de tri de sélection, avec des exemples FAQ (Foire aux questions)
Qu’est-ce’est-ce que le tri par sélection ?
Le tri par sélection est un algorithme de tri simple qui trie un tableau d’éléments dans l’ordre croissant ou décroissant. Pour ce faire, il parcourt le tableau pour trouver l’élément minimum et l’échange avec l’élément d’index 0, dans un sous-tableau trié. Le sous-tableau non trié est ensuite traversé à nouveau, et l’élément minimum trouvé et échangé dans sa position correcte. L’algorithme itère ce processus jusqu’à ce que le tableau entier soit trié. Le tri par sélection est un algorithme de tri simple qui fonctionne en trouvant à plusieurs reprises l’élément minimum d’une partie non triée du tableau et en le plaçant au début de la partie triée du tableau. L’algorithme maintient deux sous-tableaux dans un tableau donné.
Quels sont les avantages du tri par sélection ?
Le tri par sélection est un algorithme très simple à comprendre et à mettre en œuvre , et est suffisant pour de très petits ensembles de données.
Quels sont les inconvénients du tri par sélection ?
Parce qu’il n’est pas très efficace, le tri par sélection est inadéquat pour traitant de grands ensembles de données. Son efficacité ne dépend pas de la distribution des entrées, mais cela signifie également qu’il est inefficace dans tous les cas, quel que soit le tri du tableau initial. Ce n’est pas non plus un algorithme stable, ce qui signifie que l’ordre relatif des éléments égaux peut ne pas être préservé. Dans l’ensemble, il existe des algorithmes de tri supérieurs dans la plupart des cas, qui peuvent mieux s’adapter à l’entrée en question.
Quelles sont les meilleures situations pour utiliser le tri par sélection ?
Le tri par sélection est mieux utilisé lorsque la taille de l’entrée est petite et que vous souhaitez une solution simple et relativement efficace. Étant donné que la complexité de l’espace est O (1), le tri par sélection présente des avantages si l’utilisation de la mémoire est quelque chose que vous devez surveiller. Comme il effectue toujours le même nombre d’itérations, il peut être plus performant que certains autres algorithmes lors du tri d’un tableau déjà partiellement trié, car il est préférable de prendre le même temps que de prendre plus de temps. Si vous n’avez pas besoin d’un algorithme de tri stable, le tri par sélection est un choix viable.
Quelle est la complexité temporelle du tri par sélection ?
Le temps la complexité du tri par sélection est quadratique, représentée par O(n2).
Quelle est la complexité spatiale du tri par sélection ?
La complexité spatiale est O( 1). Cela signifie qu’une quantité constante de mémoire est utilisée pour chaque itération, puisqu’une seule variable temporaire doit être stockée. Bien que l’algorithme puisse être inefficace, la complexité de l’espace signifie qu’il présente des avantages dans les situations où l’utilisation de la mémoire est limitée.
Quelles sont les alternatives au tri par sélection ?
De nombreux autres algorithmes de tri seront plus efficaces dans la plupart des cas d’utilisation. Ceux-ci incluent le tri par fusion, le tri rapide et le tri par tas. Ces algorithmes ont tendance à être plus adaptatifs et ont une bien meilleure complexité temporelle. Parmi ces alternatives, le tri par fusion est le seul algorithme stable, il est donc viable là où vous devez préserver l’ordre relatif d’éléments égaux.
Le tri par sélection est-il un algorithme stable ?
Non, ce n’est pas un algorithme stable. Cela signifie que, lors du tri d’un tableau, les éléments de valeur égale peuvent ne pas être conservés dans leur ordre d’origine après l’échange.