Il existe en fait deux façons d’implémenter le tri par fusion : l’approche descendante et l’approche ascendante. C’est le bon moment pour donner un bref aperçu de ces processus.
L’approche descendante
Comme son nom l’indique, cet algorithme commence en haut avec le tableau initial, divise le tableau en deux, trie récursivement ces sous-tableaux (c’est-à-dire en les divisant et en répétant le processus), puis fusionne les résultats dans un tableau trié.
L’approche ascendante
D’autre part, l’approche ascendante repose sur une méthode itérative. Il commence par un tableau d’un seul élément, puis fusionne les éléments de chaque côté tout en les triant. Ces tableaux combinés et triés sont fusionnés et triés jusqu’à ce qu’un seul élément reste dans le tableau trié. La principale différence est que, tandis que l’approche descendante trie chaque sous-tableau de manière récursive, l’approche ascendante décompose le tableau en tableaux singuliers. Ensuite, chaque tableau est trié et fusionné de manière itérative.
Fonctionnement du tri par fusion
Suite à cela, un exemple pratique de la façon dont le tri par fusion est utilisé serait utile.
Disons que nous avoir un tableau, arr. Arr=[37, 25, 42, 2, 7, 89, 14].
Tout d’abord, nous effectuons une vérification pour voir si l’indice de gauche du tableau est inférieur à l’indice de droite. Si cela est vrai, le point médian est calculé. Ceci est égal à”(start_index”+ (“end_index”-1))/2, qui, dans ce cas, est 3. Par conséquent, l’élément à l’index 3 est le point médian, qui est 2.
Ainsi, ce tableau de 7 éléments a été scindé en deux tableaux de taille 4 et 3 pour les sous-tableaux gauche et droit respectivement:
Tableau gauche=[37, 25, 42, 2]
Right array=[7, 89, 14]
Nous continuons en calculant à nouveau le milieu et en divisant les tableaux en deux jusqu’à ce que la division ne soit plus possible. Le résultat final est :
[37], [25], [42], [2], [7], [89], [14]
Et puis, nous peut commencer à fusionner et à trier ces sous-tableaux en tant que tels :
[25, 37], [2, 42], [7,89], [14]
Ces sous-tableaux sont ensuite fusionnés et triés à nouveau pour donner :
[2, 25, 37, 45] et [7, 14, 89]
Enfin, ces sous-tableaux sont fusionnés et triés pour donner le tri final tableau :
[2, 7, 14, 25, 37, 45, 89]
Mise en œuvre du tri par fusion
Nous avons maintenant expliqué comment l’algorithme de tri par fusion fonctionne, les étapes impliquées et le travail derrière avec un exemple. Il est donc enfin temps de voir comment implémenter cet algorithme à l’aide de code. À des fins d’illustration, nous utiliserons le langage de programmation Python. Le processus peut être décrit à l’aide du code suivant:
def mergeSort(arr): if len(arr) > 1: mid=len(arr)//2 L=arr[:mid] R=arr[mid: ] mergeSort(L) mergeSort(R) i=j=k=0 tandis que i len(L) et j len(R): si L[i]=R[j]: arr[k]=L[i] i +=1 sinon : arr[k]=R[i] j +=1 k +=1 tandis que je len(L) : arr[k]=L[i] i +=1 k +=1 tandis que j len( R): arr[k]=R[j] j +=1 k +=1 def printList(arr): for i in range(len(arr)): print(arr[i], end=””) print () if__name__==’__main__’ : arr=12, 11, 13, 5, 6, 7] print(“Le tableau donné est”, end=”\n”) printList(arr) mergeSort(arr) print(“Trié array is”, end=”\n”) printList(arr)
Cela ressemble à beaucoup de code, mais c’est gérable si nous le décomposons.
Explication du code
Tout d’abord, nous définissons la fonction mergeSort en fonction du tableau”arr”.
La première instruction”if”vérifie si la longueur du tableau est supérieure à 1. Si c’est le cas, nous pouvons procéder à la division du tableau.
Ensuite, nous calculons le milieu du tableau et le divisons en deux sous-tableaux,”L”et”R”.
La fonction mergeSort est appelée de manière récursive sur L et R, en les divisant jusqu’à ce que chaque sous-tableau ne contienne qu’un seul élément.
À ce stade, trois variables sont initialisées à zéro=i, j et k. Les deux premiers sont les indices de début et de fin du sous-réseau en cours d’opération.”k”est une variable qui garde la trace de la position actuelle dans le tableau.
La partie suivante, commençant par l’instruction”while”, est la section principale de l’algorithme. L’algorithme est itéré sur L et R, en comparant les éléments à i et j et en copiant le plus petit élément dans le tableau. Avec k, ces variables d’index sont incrémentées, selon l’opérateur d’incrémentation”=-“.
La section suivante des instructions”while”dicte que tous les éléments restants dans les deux tableaux sont copiés dans le tableau initial.
Nous avons presque terminé. Ensuite, nous définissons la fonction printlist en fonction du tableau”arr”.
Enfin, nous utilisons la ligne”if_name_==’_main_'”pour s’assurer que le code n’est exécuté que lorsque le script est s’exécute directement, et non lorsqu’il est importé.
Le tableau d’origine est imprimé sous la forme”Le tableau donné est”, et le tableau final trié est imprimé sous la forme”Le tableau trié est”. La dernière ligne imprime ce tableau trié, après que le tableau initial a été trié par fusion selon le code précédent.
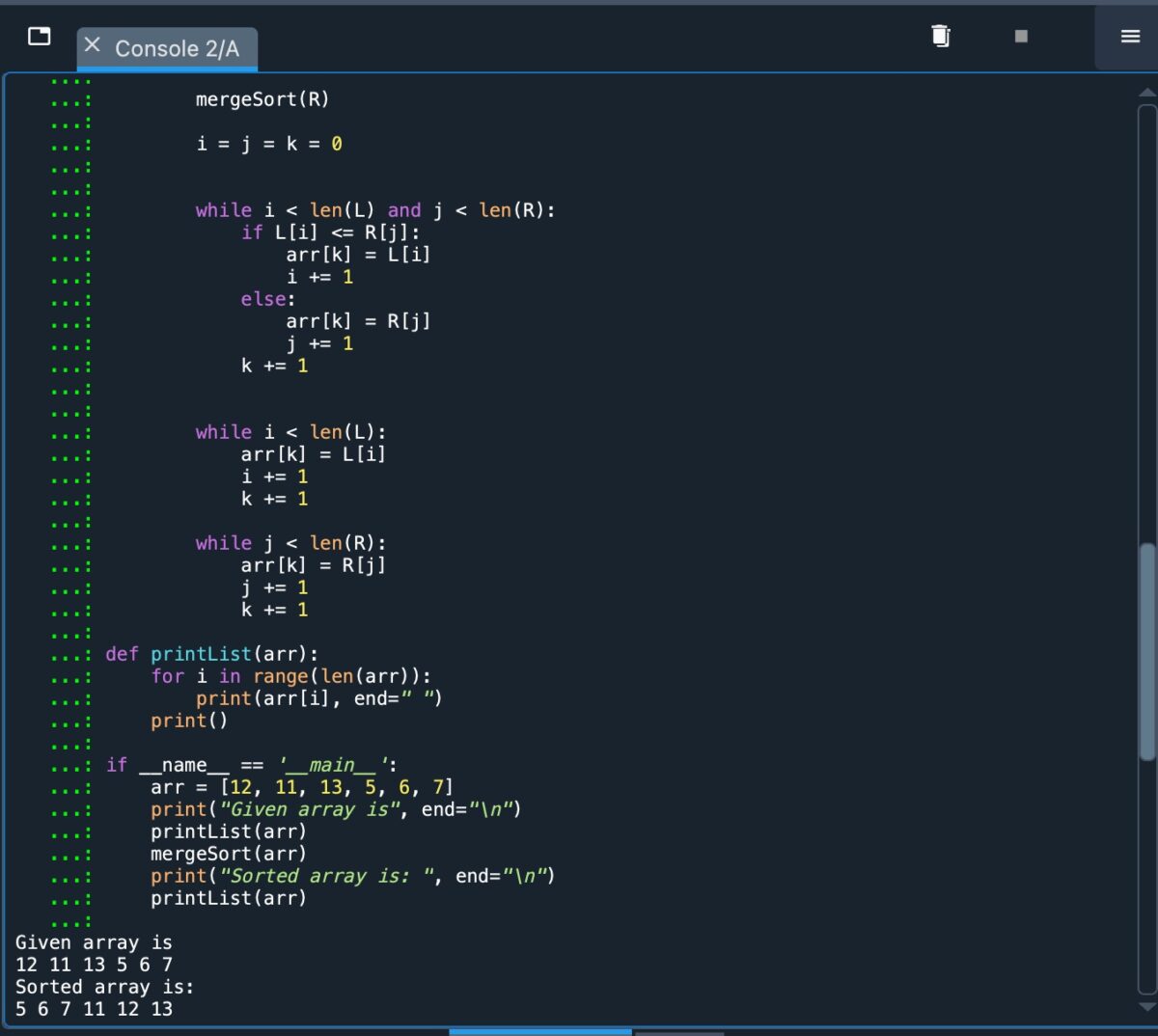
Pour conclure, voici une capture d’écran montrant ce code implémenté en Python :
Code Python pour l’algorithme de tri par fusion.
©”TNGD”.com
Les meilleurs et les pires cas d’utilisation du tri par insertion
Le tri par fusion est un algorithme simple, mais, comme pour tout algorithme , a ses meilleurs cas d’utilisation et ses pires cas. Celles-ci sont illustrées ci-dessous en termes de complexité temporelle et de complexité spatiale.
Complexité temporelle avec tri par insertion
La complexité temporelle dans chaque cas peut être décrite dans le tableau suivant :
Le meilleur cas se réfère au moment où le tableau est partiellement trié, le cas moyen se réfère au moment où le tableau est confus et le pire des cas se réfère au moment où le tableau est dans l’ordre croissant ou décroissant, et vous voulez le contraire. En tant que tel, cela nécessiterait le plus de tri.
Heureusement, le tri par fusion a la même complexité temporelle dans chaque cas, de O(n log n). En effet, dans chaque cas, chaque élément doit être copié et comparé. Cela conduit à une dépendance logarithmique sur la taille d’entrée puisque le tableau est divisé de manière récursive jusqu’à ce que chaque sous-tableau contienne un élément. En ce qui concerne les algorithmes de tri, la complexité temporelle du tri par fusion est meilleure que celle de certains autres, tels que le tri par insertion et le tri par sélection. En tant que tel, le tri par fusion est l’un des meilleurs algorithmes de tri pour travailler avec de grands ensembles de données.
Nous examinerons ensuite la complexité spatiale du tri par fusion.
Complexité spatiale du tri par fusion
Comparé à d’autres algorithmes de tri, la complexité spatiale du tri par fusion n’est pas aussi bonne C’est parce que, au lieu d’une complexité de O (1) (où l’utilisation de la mémoire est constante et une seule variable temporaire est stockée), le tri par fusion a une complexité spatiale de O (n), où n est la taille d’entrée. Dans le pire des cas, n/2 tableaux temporaires doivent être créés, chacun ayant une taille de n/2. Cela signifie qu’il y a un besoin d’espace de O(n2/4), ou O(n2). Mais, dans la moyenne et dans le meilleur des cas, le nombre de tableaux nécessaires est log(n) base 2, ce qui signifie que la complexité est proportionnelle à n. Dans l’ensemble, la complexité du tri par fusion est relativement bonne et l’algorithme convient aux grands ensembles de données, mais l’utilisation de la mémoire est plus importante que les autres méthodes.
Récapitulation
En conclusion, les avantages et les inconvénients de l’algorithme de tri par fusion ont été expliqués, ainsi que le fonctionnement de l’algorithme, illustré par des exemples. Le tri par fusion est un algorithme de tri approprié pour les grands ensembles de données, même si son utilisation de la mémoire est relativement élevée. En bref, c’est un algorithme relativement simple à comprendre et excellent à mettre en œuvre dans de nombreux environnements.