© whiteMocca/Shutterstock.com
Les algorithmes de tri se divisent généralement en deux camps : faciles à mettre en œuvre ou plus rapides à exécuter. Le tri rapide tombe principalement dans cette dernière catégorie. Lisez la suite pour savoir comment implémenter cet algorithme et les meilleures situations pour l’utiliser.
Qu’est-ce que le tri rapide ?
Le tri rapide est un algorithme de tri utilisé pour organiser des tableaux de données. Il repose essentiellement sur le principe connu sous le nom de diviser pour mieux régner. C’est la méthode par laquelle nous décomposons un problème plus gros et plus complexe en sous-problèmes plus simples. Ces sous-problèmes sont ensuite résolus et les solutions sont combinées pour trouver la solution au problème d’origine.
L’algorithme derrière le tri rapide
Ce n’est pas exactement comment implémenter le tri rapide, mais donne une idée de la façon dont il fonctionne.
//i-> Index de départ, j–> Index de fin Quicksort(array, i, j) { if (i j) { pIndex=Partition(A, i, j) Quicksor(A,i, pIndex-1) Quicksort(A,pIndex+1, end) } }
Tout d’abord, nous définissons le tri rapide comme une fonction d’un tableau avec un élément de départ et un élément de fin. L’instruction”if”vérifie que le tableau contient plus d’un élément.
Dans ce cas, nous appelons la fonction”partition”, qui nous donne l’index de l’élément”pivot”. Cela sépare le tableau en deux sous-tableaux, avec des éléments plus petits et plus grands que le pivot respectivement.
La fonction est appelée de manière récursive sur chaque sous-tableau, jusqu’à ce que chaque sous-tableau n’ait qu’un seul élément. Le tableau trié est ensuite renvoyé et le processus est terminé.
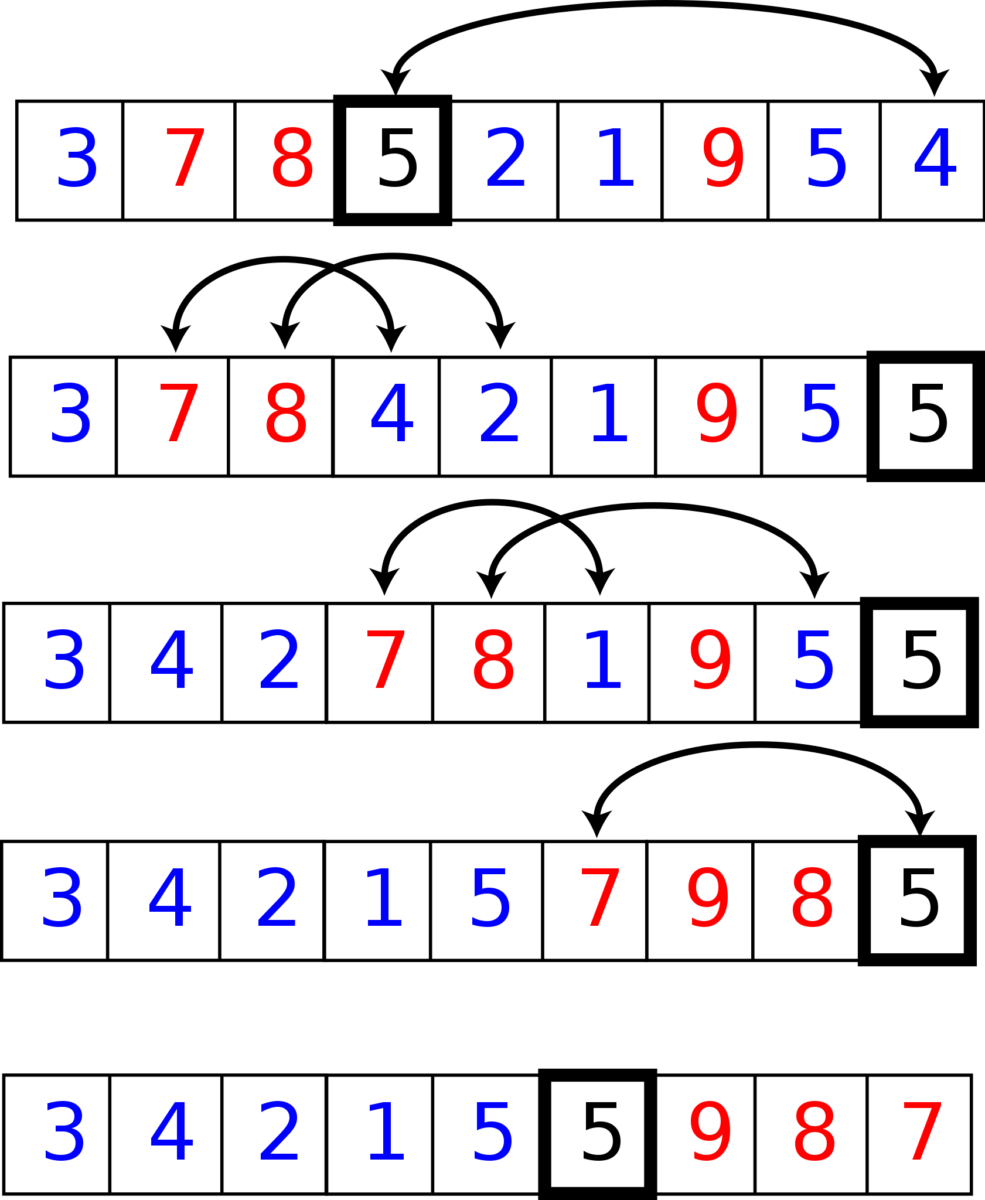 Dans cet exemple, l’élément encadré est l’élément pivot, les éléments bleus sont égaux ou inférieurs et les éléments rouges sont supérieurs.
Dans cet exemple, l’élément encadré est l’élément pivot, les éléments bleus sont égaux ou inférieurs et les éléments rouges sont supérieurs.
©Dcoetzee/Public Domain – Licence
Un exemple de tri rapide
Comme avec la plupart des choses, rapide sort est mieux expliqué en utilisant un exemple pour illustrer.
Prenons le tableau suivant-[56, 47, 98, 3, 6, 7, 11]
Nous avons indices de 0 à 6 (rappelez-vous que le premier élément est l’indice 0, pas 1).
En prenant le dernier élément comme pivot, le tableau est réorganisé de sorte que les éléments plus petits que le pivot soient à gauche, et les grands éléments sont à droite. Cela se fait en initialisant les variables i et j à 0. Si arr[j], ou l’élément actuel, est plus petit que le pivot, nous l’échangeons avec arr[i] et le faisons de manière incrémentielle. Le pivot est ensuite échangé avec arr[i] pour que cet élément soit dans sa position triée.
Cela donne les sous-tableaux [6, 7, 3] et [56, 47, 98]. L’indice de l’élément pivot est maintenant 3 au lieu de 6.
Le tri rapide est alors appelé, qui trie le sous-tableau de gauche autour de l’élément pivot, 3, en triant les sous-tableaux [6] et [7].
Nous appelons ensuite le tri rapide de manière récursive sur le bon sous-tableau, de sorte qu’il soit trié en [47, 56, 98].
Enfin, les sous-tableaux sont combinés pour donner le tableau trié-[3, 6, 7, 11, 47, 56, 98].
Implémentation
Maintenant que nous avons couvert la base du tri rapide, implémentons-le en utilisant Python. Le code que nous utilisons peut être décrit comme suit :
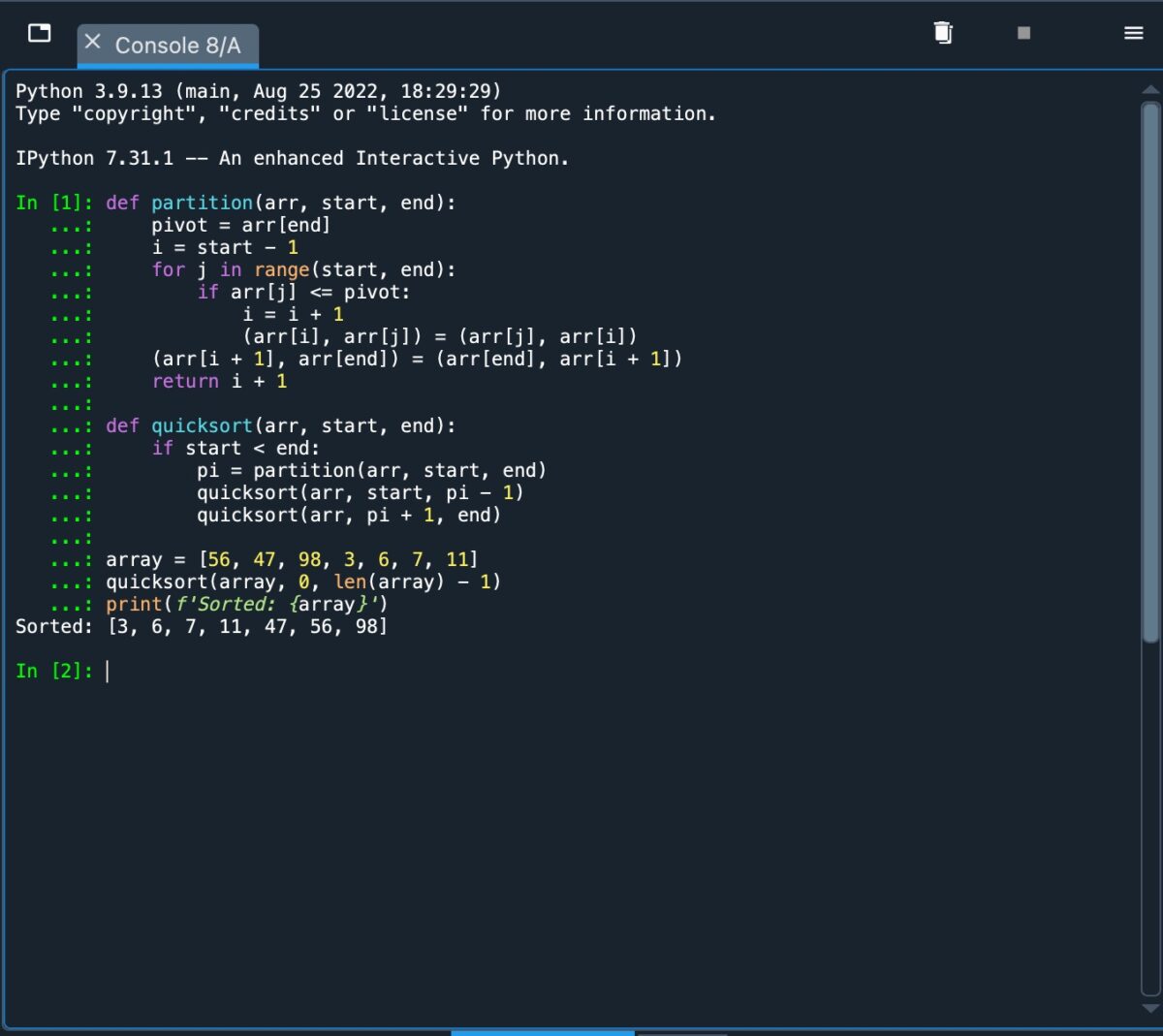
def partition(arr, start, end): pivot=arr[end] i=start-1 for j in range(start, end): if arr[j]=pivot : je=je + 1 (arr[i], arr[j]=(arr[j], arr[i]) (arr[i + 1], arr[fin])=(arr[fin], arr[i + 1]) return i + 1 def quicksort(arr, start, end): if start end: pi=partition(arr, start, end) quicksort(arr, start, pi-1) quicksort(arr, pi + 1, end) array=[56, 47, 98, 3, 6, 7, 11] quicksort(array, 0, len(array)-1) print(f’Sorted: {array}’)
First , nous définissons une fonction de partition en fonction d’un tableau, avec un index de début et de fin.
La valeur pivot est alors définie sur le dernier élément du tableau, et i est initialisé au début index, moins 1.
La boucle”for”parcourt le tableau, de l’index de départ à l’index de fin moins 1.
L’instruction”if”permute l’élément actuel, j, avec la valeur à l’indice i si j est inférieur à ou eq ual au pivot. La variable i est alors incrémentée.
Après cela, le pivot est permuté avec l’élément à l’indice i+1. Cela signifie que tous les éléments à gauche du pivot lui sont inférieurs ou égaux, et les éléments à droite lui sont supérieurs.
L’indice de la valeur du pivot est alors renvoyé.
“Quicksort”est alors défini comme une fonction du tableau, et le tableau est vérifié pour s’assurer qu’il contient plus d’un élément.
La fonction”partition”est alors appelée, avec l’index valeur réglée sur”pi”. Le tri rapide est appelé de manière récursive sur les sous-tableaux gauche et droit, jusqu’à ce que chaque sous-tableau ne contienne qu’un seul élément.
Enfin, un tableau trié est créé et imprimé à l’aide de la fonction”print”.
 Le tri rapide est appelé de manière récursive à gauche et les sous-tableaux à droite, jusqu’à ce que chaque sous-tableau ne contienne qu’un seul élément.
Le tri rapide est appelé de manière récursive à gauche et les sous-tableaux à droite, jusqu’à ce que chaque sous-tableau ne contienne qu’un seul élément.
©”TNGD”.com
Les meilleurs et les pires cas d’utilisation du tri rapide
Alors que la théorie derrière le tri rapide peut semblent compliqués au premier abord, l’algorithme présente de nombreux avantages et est généralement assez rapide. Examinons la complexité temporelle et spatiale du tri rapide.
Complexité temporelle du tri rapide
Le tableau résume la complexité temporelle du tri rapide.
Le meilleur cas est lorsque la partition est équilibrée, où le pivot est proche ou égal à la valeur médiane. Ainsi, les deux sous-réseaux sont de taille similaire et n opérations sont effectuées à chaque niveau. Cela conduit à une complexité temporelle logarithmique.
Lorsque l’élément pivot est relativement proche, c’est le cas moyen. La complexité temporelle est la même que dans le meilleur des cas puisque les tableaux sont à peu près égaux en taille.
Cependant, le pire des cas transforme la complexité temporelle en temps quadratique. En effet, le réseau est très déséquilibré, où le pivot est proche de l’élément minimum ou maximum. Cela provoque une situation dans laquelle les sous-réseaux sont de taille très inégale, l’un d’entre eux ne contenant qu’un seul élément. En tant que tel, il existe n niveaux de récursivité ainsi que n opérations, conduisant à une dépendance quadratique sur la taille d’entrée.
Complexité spatiale du tri rapide
Un autre facteur à prendre en compte est l’espace complexité du tri rapide. Cela peut être résumé comme suit :
La complexité de l’espace pour le tri rapide est la même pour le meilleur et pour la moyenne cas. En effet, l’algorithme a des niveaux récursifs log n et chaque appel récursif utilise une quantité constante d’espace mémoire. En tant que tel, l’espace mémoire total est proportionnel à la profondeur de l’arbre de récursivité.
Dans le pire des cas, cependant, la complexité de l’espace est modifiée en O(n). Parce que l’arbre de récursivité est considérablement déséquilibré, ce qui signifie qu’il y a n appels récursifs.
Récapitulatif
Dans l’ensemble, le tri rapide est, comme son nom l’indique, un moyen très efficace de trier un tableau, en particulier les plus grands. Une fois le processus compris, il est relativement facile à mettre en œuvre et à modifier. Il est utile dans un large éventail de scénarios et constitue une bonne base pour des algorithmes de tri plus complexes.
Suivant…
Qu’est-ce que le tri rapide et comment ça marche ? (Avec exemples) FAQ (Foire aux questions)
Qu’est-ce que le tri rapide ?
Le tri rapide est un algorithme de tri permettant de trier des tableaux de données. Cela fonctionne en sélectionnant un élément pivot et en divisant le tableau en deux sous-tableaux, un avec des éléments plus petits que le pivot et un avec des éléments plus grands. Ce processus est répété de manière récursive jusqu’à ce que chaque sous-tableau soit trié et ne contienne qu’un seul élément. Les tableaux sont ensuite combinés pour donner un tableau trié.
Le tri rapide est-il un algorithme stable ?
Le tri rapide est généralement un algorithme instable. Cela signifie que l’ordre relatif des éléments égaux peut ne pas être conservé dans la sortie finale.
Comment choisir l’élément pivot avec tri rapide ?
Vous pouvez choisir le premier ou le dernier élément, ou faire un choix aléatoire. Avec des ensembles de données particulièrement volumineux, la randomisation du choix conduit généralement à de bonnes performances.
Quelle est la complexité temporelle du tri rapide ?
Le meilleur cas et le cas moyen est O(n log n), tandis que le pire des cas est O(n2).
Quelle est la complexité spatiale du tri rapide ?
Le meilleur et les cas moyens sont O(log n), alors que le pire des cas est O(n).
Quels sont les meilleurs cas pour utiliser le tri rapide ?
Le tri rapide peut être utilisé pour de nombreux types de tableaux, mais parfois, des alternatives telles que le tri par tas ou le tri par fusion peuvent mieux fonctionner, compte tenu de certaines contraintes. C’est généralement là que vous avez besoin d’un algorithme stable comme le tri par fusion, ou lorsque le temps est un facteur. Par exemple, la complexité temporelle du cas le plus défavorable du tri par tas est aussi bonne que la complexité temporelle moyenne du cas du tri rapide. Des algorithmes plus simples comme le tri par sélection ou par insertion peuvent également être plus rapides pour les petits ensembles de données.