© TippaPatt/Shutterstock.com
Les informaticiens utilisent souvent des graphiques pour représenter des données. Les graphiques peuvent représenter diverses relations, des cartes et des composés chimiques aux relations sociales et aux réseaux informatiques. Nous pouvons utiliser de nombreux algorithmes avec des graphes, tels que l’algorithme de Dijkstra, le Depth-First Search (DFS) et l’algorithme Breadth-First Search (ou BFS). Bien que vous puissiez utiliser les deux algorithmes pour parcourir les nœuds d’un graphe, BFS est préférable pour les graphes non pondérés. Dans cet article, nous allons explorer le fonctionnement de BFS et ses applications.
Qu’est-ce que BFS ?
BFS est un algorithme de recherche. L’algorithme commence sa traversée au nœud source, puis visite les nœuds voisins. Après cela, l’algorithme choisit le nœud le plus proche au niveau de profondeur suivant, puis visite les nœuds inexplorés à côté de celui-ci, et ainsi de suite. Étant donné que l’algorithme BFS visite les nœuds à chaque niveau avant de passer au niveau suivant, c’est de là que vient le nom”Breadth-first”. Nous nous assurons de ne visiter chaque nœud qu’une seule fois en suivant les nœuds visités et non visités. Vous pouvez utiliser BFS pour calculer les distances de chemin, tout comme avec l’algorithme de Dijkstra.
L’algorithme derrière BFS
Nous pouvons représenter l’algorithme de base avec le pseudocode suivant :
BFS(graph, start): file d’attente=[démarrer] visité=définir (démarrer) tant que la file d’attente n’est pas vide : nœud=retirer de la file d’attente (file d’attente) traiter (nœud) pour le voisin dans le graphe. voisins (nœud) : si le voisin n’est pas visité : visité. ajouter (le voisin) enqueue(queue, neighbor)
Dans ce cas, nous définissons un graphe comme”graphe”, et”start”est le nœud de départ.
Nous implémentons une structure de file d’attente pour contenir les nœuds non visités , ainsi qu’un ensemble”visité”pour contenir les nœuds visités.
La boucle”while”continue jusqu’à ce que la file d’attente soit vide, et lance le traitement des nœuds niveau par niveau. La fonction”dequeue”supprime le premier nœud de la file d’attente au fur et à mesure qu’il est visité.
La fonction”process”exécute une fonction souhaitée sur le nœud, telle que la mise à jour de la distance à ses voisins ou l’impression de données sur la console.
La boucle”for”itère sur tous les voisins du nœud actuel, vérifiant si le nœud a déjà été visité. Sinon, il est ajouté à la file d’attente à l’aide de la fonction”mettre en file d’attente”. Essentiellement, les nœuds à chaque niveau sont stockés dans la file d’attente, avec leurs voisins ajoutés pour être visités au niveau de profondeur suivant. Cela nous permet de déterminer le chemin le plus court entre le nœud source et tous les autres nœuds du graphe.
Le fonctionnement de BFS
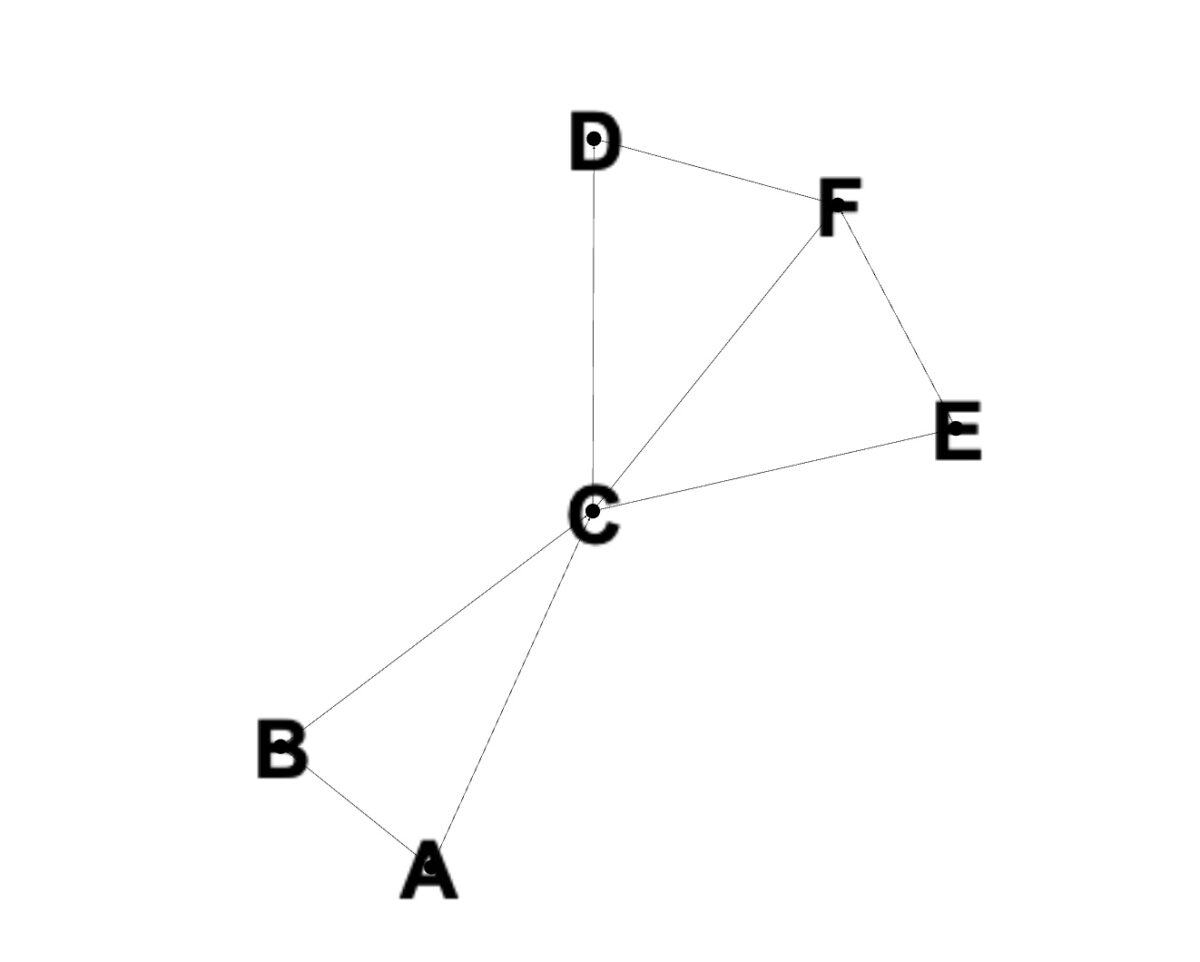Nous utiliserons ce graphique pour les exemples de code suivants.
©”TNGD”.com
Après avoir expliqué les bases, il est temps de voir comment BFS fonctionne en pratique. Nous allons illustrer cela à l’aide d’un graphique avec les nœuds A, B, C, D, E et F, comme indiqué dans l’image. Le code ci-dessous montre comment implémenter BFS pour ce graphe en utilisant le langage de programmation Python.
from collections import defaultdict, deque def bfs(graph, start): queue=deque([start]) visitor=set([start] ) while queue : nœud=queue.popleft() print(nœud) pour le voisin dans le graphe[nœud] : si le voisin n’est pas visité : visited.add(neighbor) queue.append(neighbor) graph=defaultdict(list) edge=[ (“A”,”B”),”A”,”C”), (“B”,”C”), (“C”,”D”), (“C”,”E”), (“C”,”F”), (“D”,”F”), (“E”,”F”) pour les arêtes dans les arêtes : graph[edge[0]].append(edge[0]) graph[ edge[1]].append(edge[0]) bfs(graph,”A”)
Explication du code
Tout d’abord, nous importons les classes”defaultdict”et”deque”du module « collections ». Celles-ci sont utilisées pour créer un dictionnaire avec des valeurs de clé par défaut et pour créer une file d’attente permettant d’ajouter et de supprimer des éléments.
Ensuite, nous définissons la fonction”bfs”avec deux arguments,”graph”et”commencer”. Nous prenons l’argument”graphe”comme un dictionnaire avec les sommets comme clés et les sommets voisins comme valeurs. Ici,”start”fait référence au nœud source, où l’algorithme commence.
“queue=deque([start])”crée une file d’attente avec le nœud source comme seul élément, et”visited=set ([début]) » crée un ensemble de nœuds visités avec le nœud source comme seul élément.
La boucle « while » continue jusqu’à ce que la file d’attente soit vide.”node=queue.popleft()”supprime l’élément le plus à gauche de la file d’attente et le stocke dans la variable”node”.”print(node)”imprime ces valeurs de nœud.
La boucle”for”itère sur chaque nœud voisin.”si voisin non visité”vérifie si le voisin a été visité.”visited.add(neighbor)”ajoute le voisin à la liste visitée, et”queue.append(neighbor)”ajoute le voisin à l’extrémité droite de la file d’attente.
Après cela, nous créons une valeur par défaut dictionnaire appelé « graphe », et définir les arêtes du graphe. La boucle”for”itère sur chaque arête.”graph[edge[0]].append(edge[1])”ajoute le deuxième élément de l’arête comme voisin du premier élément, et le premier élément de l’arête comme voisin du second. Cela construit le graphe.
Enfin, nous appelons la fonction”bfs”sur”graph”, avec le nœud source comme”A”.
Mise en œuvre du code
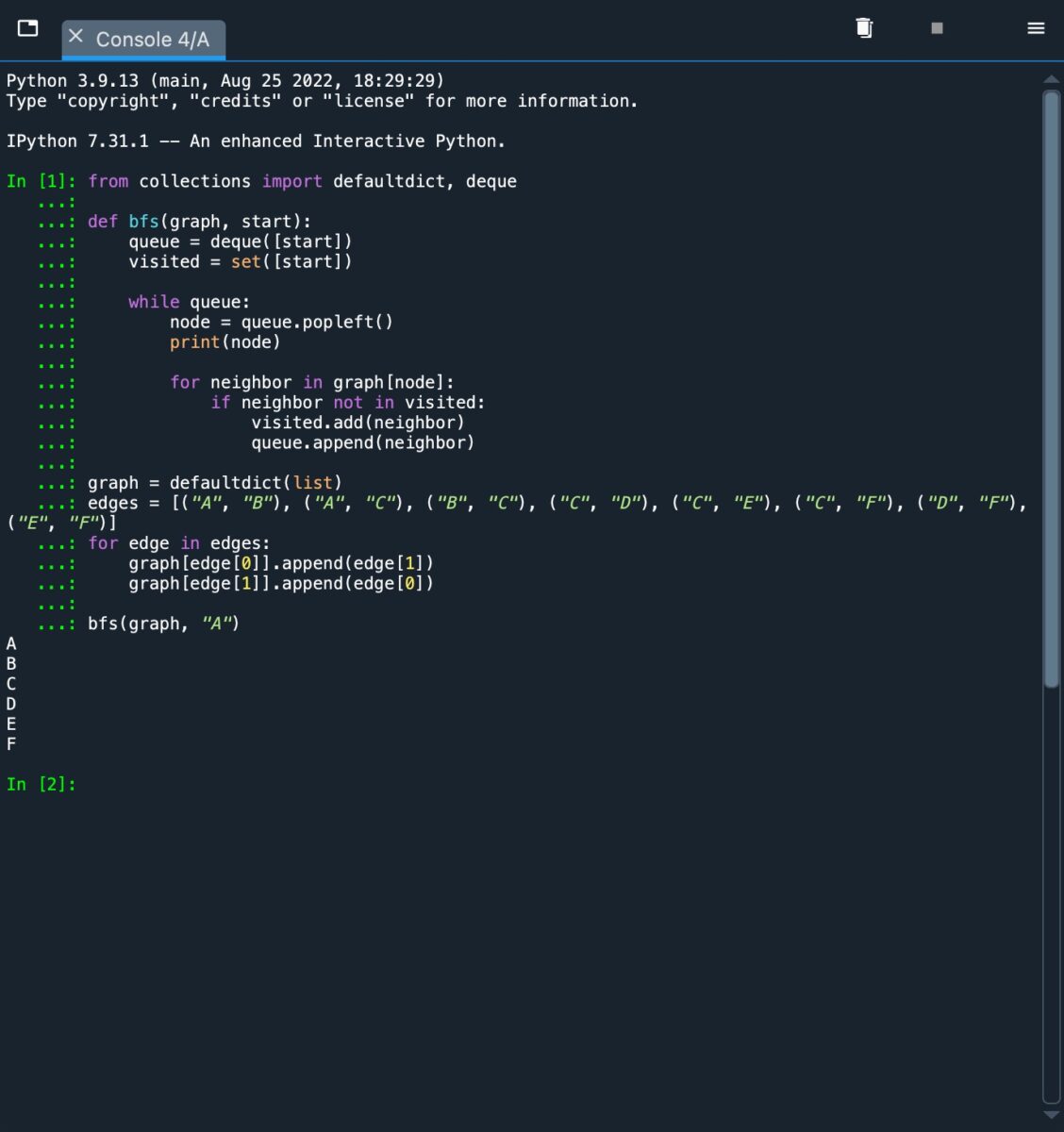Voici à quoi ressemble l’algorithme BFS lorsque implémenté et exécuté via un graphe connecté.
©”TNGD”.com
Dans la capture d’écran, nous pouvons voir la sortie [A, B, C, D, E F]. C’est ce à quoi nous nous attendions puisque BFS explore les nœuds à chaque niveau de profondeur avant de passer au suivant. En revenant au graphique, nous voyons que B et C seront ajoutés à la file d’attente et visités en premier. B est visité, puis A et C sont ajoutés à la file d’attente. Puisque A a déjà été visité, C est visité ensuite et A est supprimé. Après cela, les voisins de C, D, E et F, sont ajoutés à la file d’attente. Ceux-ci sont ensuite visités et la sortie est imprimée.
Utilisation de BFS pour les graphes déconnectés
Nous avons précédemment utilisé BFS pour un graphe connecté. Cependant, nous pouvons également utiliser BFS lorsque les nœuds ne sont pas tous connectés. Nous allons utiliser les mêmes données de graphique puisque l’algorithme modifié peut être illustré avec l’un ou l’autre type de graphique. Le code modifié est:
from collections import defaultdict, deque def bfs(graph, start): queue=deque([start]) visitor=set([start]) while queue: node=queue.popleft() print (nœud) pour le voisin dans le graphe [nœud] : si le voisin n’est pas visité : visited.add(neighbor) queue.append(neighbor) pour le nœud dans le graphe. ]). defaultdict(list) edge=[(“A”,”B”), (“A”,”C”), (“B”,”C”), (“C”,”D”), (“C”,”E”), (“C”,”F”), (“D”,”F”), (“E”,”F”)] pour les arêtes dans les arêtes : graph[edge[0]]. ajouter(bord[1]) graphique[bord[1]].append(bord[0]) bfs(graph,”A”)
Nous avons utilisé une boucle”for”supplémentaire. La boucle itère sur tous les nœuds en utilisant la méthode”graph.keys()”. BFS démarre une nouvelle file d’attente s’il trouve un nœud non visité et fonctionne de manière récursive. En faisant cela, nous visitons tous les nœuds déconnectés. Voir l’image ci-dessous pour une illustration.
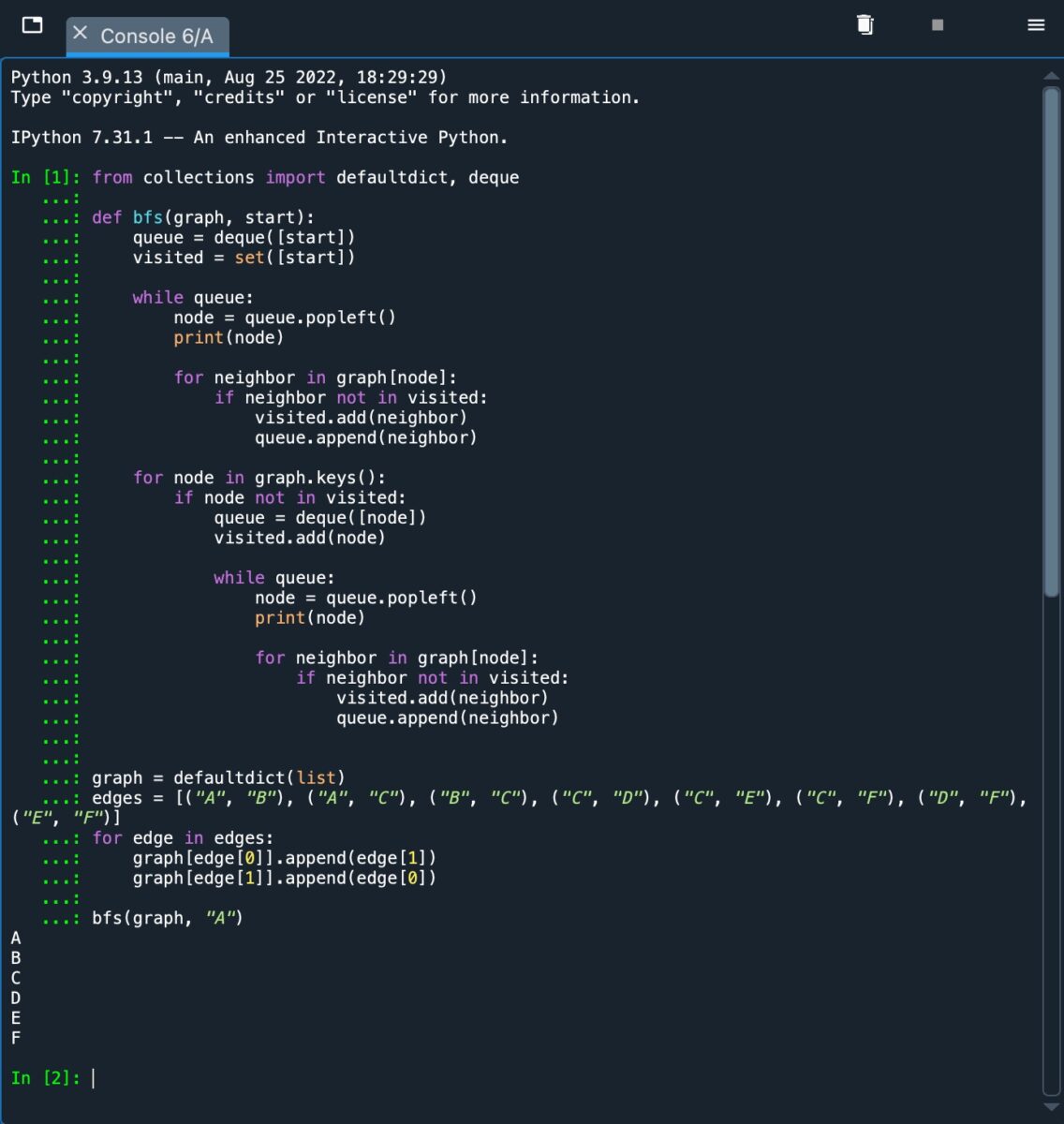Ceci est un exemple de l’algorithme BFS lorsqu’il est implémenté et exécuté sur un graphe déconnecté.
©”TNGD”.com
Meilleurs et pires cas d’utilisation pour BFS
Maintenant que nous savons comment fonctionne BFS, nous devons examiner la complexité temporelle et spatiale de l’algorithme pour avoir une idée de ses meilleurs et pires cas d’utilisation.
Complexité temporelle de BFS
Nous pouvons voir que la complexité temporelle est la même dans tous les cas, et est égale à O(V + E), où V est le nombre de sommets et E est le nombre d’arêtes. Dans le meilleur des cas, où nous n’avons qu’un seul nœud, la complexité sera O(1), car V=1 et E=0. Dans le cas moyen et le pire, l’algorithme visite tous les nœuds qu’il peut atteindre depuis le nœud source , donc la complexité dépend de la structure et de la taille du graphe dans les deux cas.
Complexité spatiale de BFS
Encore une fois, nous voyons que la complexité est la même pour tous les cas. L’algorithme visite chaque nœud quelle que soit la structure du graphe. Par conséquent, la complexité dépend du nombre de sommets dans le graphe.
Récapitulation
BFS est un moyen de traverser les nœuds d’un graphe, de calculer les distances de chemin et d’explorer les relations entre nœuds. C’est un algorithme très utile pour explorer les systèmes de réseau et détecter les cycles de graphes. BFS est relativement facile à mettre en œuvre pour les graphes connectés et déconnectés. L’avantage est que la complexité temporelle et spatiale est la même pour tous les cas.
Breadth-First Search (BFS) for Graphs – Explique, avec des exemples de FAQ (Foire aux questions)
Qu’est-ce que BFS ?
BFS est un algorithme utilisé pour parcourir des arbres ou des graphiques, généralement ceux représentant des réseaux tels que les réseaux sociaux ou informatiques. Il peut également détecter les cycles de graphe ou si un graphe est bipartite, ainsi que calculer les distances de chemin les plus courtes. La largeur d’abord signifie que chaque nœud est exploré à un niveau de profondeur particulier avant de passer au suivant.
Quelle est la complexité temporelle de BFS ?
La la complexité temporelle de BFS est O(V + E) dans tous les cas.
Quelle est la complexité spatiale de BFS ?
La complexité spatiale de BFS est O(V) dans tous les cas.
Quand utiliser BFS ?
Si vous devez calculer la distance du chemin le plus court ou explorer tous les sommets dans un graphique non pondéré.
Comment BFS est-il implémenté ?
Nous implémentons généralement BFS en utilisant une structure de données de file d’attente et un ensemble pour garder une trace des nœuds visités et non visités. Le nœud source est ajouté à la file d’attente et marqué comme visité. Ensuite, l’algorithme fonctionne de manière récursive sur les nœuds voisins, ajoutant et supprimant des nœuds au fur et à mesure pour s’assurer qu’aucun nœud n’est visité deux fois.
Comment BFS se compare-t-il à l’algorithme de Dijkstra ?
Ces algorithmes peuvent tous deux être utilisés pour calculer les distances des chemins les plus courts, mais BFS fonctionne avec des graphiques non pondérés. En revanche, l’algorithme de Dijkstra fonctionne avec des graphiques pondérés.
Comment DFS se compare-t-il à BFS ?
Les deux sont utilisés pour parcourir un graphique, mais ils diffèrent dans comment ils font ça. Alors que BFS recherche chaque nœud à un niveau de profondeur donné avant de continuer, DFS visite les nœuds aussi loin que possible avant de revenir sur lui-même pour explorer une autre branche. DFS utilise généralement une structure de données de pile par opposition à une file d’attente.