© NicoElNino/Shutterstock.com
En informatique, les données peuvent être structurées et parcourues de différentes manières. Les arbres binaires sont une forme de stockage de données hiérarchique qui utilise les traversées d’arbres comme méthode principale pour visiter tous les nœuds constitutifs à des fins de recherche, de tri et à d’autres fins. Comprendre les différentes méthodes utilisées pour les parcours d’arbres peut vous aider à effectuer des opérations de base sur un arbre binaire. Dans cet article, nous expliquons ce que sont les traversées d’arbres, y compris les traversées d’ordre, de préordre et de post-ordre, avec des exemples pour vous aider à démarrer.
Qu’est-ce que les traversées d’arbre ?
Les traversées d’arbres sont les méthodes utilisées par les informaticiens, les développeurs et les ingénieurs en logiciel pour parcourir un arbre binaire. Il est également connu sous le nom :
Parcourir l’arborescence Recherche dans l’arborescence
Ces méthodes impliquent de visiter séquentiellement chaque nœud de l’arbre binaire. Contrairement à une structure de données linéaire comme une liste chaînée ou une file d’attente, ces parcours peuvent être effectués de différentes manières. Les principales méthodes, expliquées ci-dessous, sont utilisées pour mettre à jour, supprimer, rechercher, trier et récupérer efficacement des données.
À propos des arbres binaires
Les arbres binaires sont la forme d’arbre la plus couramment utilisée. Il s’agit d’une structure de données hiérarchique composée de nœuds interconnectés. Chaque nœud se compose de références gauche et droite et d’un élément de données. Chaque nœud d’un arbre binaire est connecté à un parent, mais chaque nœud parent ne peut avoir qu’un maximum de 2 enfants. Les nœuds sans enfants sont appelés feuilles. Les nœuds qui partagent un nœud parent sont appelés frères et sœurs. Le nœud au sommet d’un arbre binaire est appelé la racine.
Si un arbre binaire est complètement rempli, on l’appelle un arbre complet. Les arbres sont remplis de nœuds de gauche à droite. Vous pouvez positionner les nœuds par leur hauteur, qui est le nombre d’arêtes entre la racine et le nœud d’index, ou leur profondeur, qui est le nombre d’arêtes entre le nœud et le nœud feuille le plus éloigné.
Utiliser les traversées d’arbres pour visiter chaque nœud d’un arbre
Une caractéristique importante de ces traversées est que chaque nœud de l’arbre est visité. Étant donné que les arbres sont des structures de données non linéaires, il existe de nombreuses manières et ordres dans lesquels vous pouvez vous assurer que chaque nœud est visité à tour de rôle. Il n’y a pas de parcours unique, mais plusieurs algorithmes de parcours avec lesquels vous pouvez travailler.
Les parcours d’arbres sont importants
Maîtriser les parcours d’arbres est une compétence clé pour organiser et travailler avec des données. En effet, les arbres sont une structure de données extrêmement courante et sont largement utilisés en raison de leur représentation claire des relations et des hiérarchies de données.
Vous pouvez utiliser ces méthodes de parcours et ces exemples pour des recherches ou des insertions de données plus efficaces. Jetons un coup d’œil aux méthodes clés ci-dessous :
Voici un exemple d’arborescence :
Une illustration d’une arborescence.
©”TNGD”.com
1. PreOrder Traversal
Il s’agit d’un type de parcours en profondeur où le nœud parent est visité en premier, puis le nœud enfant gauche, puis le nœud enfant droit. Si un arbre est traversé à l’aide de la méthode preOrder, le nœud racine est visité en premier, puis les sous-arbres séquentiels gauche et droit parent en premier jusqu’à ce que l’arbre entier soit traversé. Le parcours de pré-ordre fournit une méthode efficace pour copier un arbre.
Voici l’exemple de parcours de pré-ordre pour l’arbre ci-dessus : A > B > D > E > C > F > G
Et voici l’algorithme de précommande:
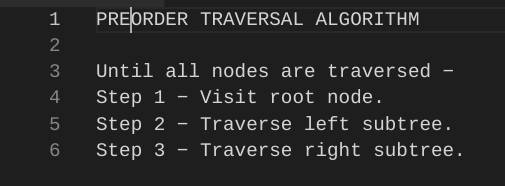Algorithme pour le PreOrder Traversal d’une arborescence.
©”TNGD”.com
2. Parcours dans l’ordre
Il s’agit d’un type de parcours en profondeur où le nœud enfant gauche est visité, puis le parent, puis le nœud enfant droit. Les traversées InOrder passent par le sous-arbre le plus à gauche et se terminent au sous-arbre le plus à droite. Ce type de parcours produit des données organisées par ordre croissant.
Voici l’exemple de parcours inOrder pour l’arbre ci-dessus : D > B > E > A > F > C > G
Et voici l’algorithme inOrder :
Algorithme pour le parcours inOrder d’une structure arborescente.
©”TNGD”.com
3. Traversée PostOrder
Ce troisième type de traversée en profondeur d’abord visite le nœud enfant gauche, puis le nœud enfant droit puis le parent. Avec la traversée de l’arbre postOrder, les sous-arbres sont tous visités en premier (en partant du bas à gauche) avec la racine visitée en dernier. La traversée PostOrder est un moyen efficace de supprimer un arbre.
Voici l’exemple de parcours postOrder pour l’arborescence ci-dessus : D > E > B > F > G > C > A
Et voici l’algorithme postOrder :
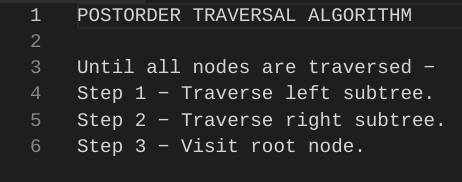Algorithme pour le postOrder Traversal d’une structure arborescente.
©”TNGD”.com
Il existe également une traversée en largeur qui visite les nœuds de haut en bas et de gauche à droite. C’est la seule forme de parcours en largeur d’abord.
Arrondissement
Comme vous pouvez le voir, les parcours d’arbres font la gestion de données hiérarchiques très simple. Les algorithmes sont simples et si vous vous égarez, vous pouvez tracer un arbre de base pour vous orienter. Ces méthodes sont si efficaces que vous pouvez construire des arbres binaires complets à partir des parcours pré et post-ordre fournis. Pratiquez ces méthodes pour les maîtriser et étendre vos connaissances.
Que sont les parcours d’arborescence (Inorder, Preorder et Postorder) – Avec des exemples FAQ (Foire aux questions)
Qu’est-ce qu’une structure de données ?
Les structures de données sont les formats spécifiques utilisés pour organiser les données afin qu’elles puissent être stockées en toute sécurité et gérées et accessibles de manière efficace.
Quels sont les principaux types d’arbres ?
Outre les arbres binaires, les principaux types d’arbres incluent :
Arbres de tas Arbres de syntaxe Essais B-trees T-trees
Qu’est-ce qu’un arbre binaire parfait ?
Un arbre binaire parfait a tous les nœuds feuilles à la même profondeur et tous les nœuds parents ont deux enfants. C’est une autre façon de décrire un arbre complètement rempli et sans lacunes.
Quels sont les exemples de structures de données non arborescentes ?
Les structures de données non arborescentes sont principalement des structures de données linéaires qui incluent :
Tableaux A bitmap Matrice Tableau parallèle Liste doublement chaînée Liste auto-organisée
Que sont les types de données abstraits ?
Les types de données abstraits (ADT) sont des modèles mathématiques qui peuvent être utilisés pour structurer les données et faciliter la programmation à grande échelle. En informatique, les ADT peuvent être utilisés pour regrouper et gérer des données pour une variété d’applications informatiques.