Bringt Ihnen das Umwandeln einer quadratischen Gleichung in die Scheitelpunktform Kopfzerbrechen? In diesem Artikel erklären wir, wie Sie in einfachen Schritten per Hand, auf Ihrem Taschenrechner oder mit einem Online-Tool in die Scheitelpunktform konvertieren.
Was ist die Scheitelpunktform?
Die Scheitelpunktform bezieht sich auf die Parabel einer Gleichung. Eine Parabel ist ein krummliniger Graph, der durch eine quadratische Funktion erzeugt wird. Parabel Unterscheidungsmerkmale, die Sie mathematisch beschreiben können. Dazu gehören:
Der Fokus ist ein fester Punkt auf der Parabel. Die Leitlinie, eine feste Linie, die senkrecht zur Achse der Parabel verläuft. Der Scheitelpunkt ist der Punkt, an dem die Kurve die Achse des Diagramms schneidet – entweder ihren niedrigsten oder höchsten Punkt.
Die Scheitelpunktform der Gleichung charakterisiert also den Schnittpunkt der Symmetrieachse in einer Parabel. Dieses Formular enthält technisch gesehen die Informationen, die Sie zum Zeichnen der Parabel der quadratischen Gleichung benötigen, ähnlich wie beim Zeichnen von Koordinaten. Die Scheitelpunktform einer Gleichung hat ein bestimmtes Format, das die Scheitelpunktdetails enthält:
y=a·(x-h)² + k.
In einer quadratischen Eckpunktgleichung sagt der Buchstabe a aus uns, ob sich die Kurve nach oben oder nach unten öffnet. h undk geben die Position des Scheitelpunkts (x-bzw. y-Koordinaten) an, wenn Sie einen Graphen dieser Gleichung erstellen würden.
Warum ist die Scheitelpunktform wichtig?
Die Parabel ist ein bahnbrechendes mathematisches Konzept mit einem breiten Anwendungsbereich. Pascal hielt es für die Projektion eines Kreises, während Galileo die Parabel mit dem Weg in Verbindung brachte, den ein Projektil unter gleichmäßiger Schwerkraft nimmt.
Parabelpfade sind in der Physik weit verbreitet, und sowohl Scheitelpunkt-als auch quadratische Gleichungen werden verwendet, um Flächen innerhalb eines geschlossenen Raums, die Geschwindigkeit und die Flugbahn von sich bewegenden physischen Körpern zu berechnen und Präzisionskurven für das Design zu erstellen.
So konvertieren Sie in einen Scheitelpunkt
Zusammengefasst können Sie eine Standardgleichung in ihre Scheitelpunktform umwandeln, indem Sie das Quadrat vervollständigen. Hier ist eine Schritt-für-Schritt-Anleitung, wie Sie das Quadrat vervollständigen und dann die Gleichung in einen Scheitelpunkt umwandeln:
Hier ist eine umzuwandelnde Standardgleichung:
y=-3×2 – 6x – 9
Um diese Gleichung in ihre Scheitelpunktform umzuwandeln, müssen Sie sich mit dem „(a+b)2 ganzen Quadrat“ befassen, das in der Standardform vorliegt. Um die Standardform wie in den folgenden Schritten erklärt umzuwandeln, vervollständigen wir das Quadrat.
Schritt 1: Identifizieren Sie den Koeffizienten von x in der Standardgleichung
Wenn der Koeffizient von x2 ist nicht eins, dieser Faktor muss als gemeinsamer Faktor außen platziert werden. Im Fall der obigen Gleichung ist es-3.
Identifiziere den Koeffizienten von x in der Standardgleichung
Schritt 2: Verschiebe den Koeffizienten aus der Formel heraus
Der Koeffizient ist der Wert, der sich außerhalb der Formel bewegt:
y=−3×2 − 6x − 9=−3 (x2 + 2x + 3)
Nun ist der Koeffizient von x2 1 und Sie können Wandeln Sie diese Gleichung leicht in ihre Scheitelpunktform um.
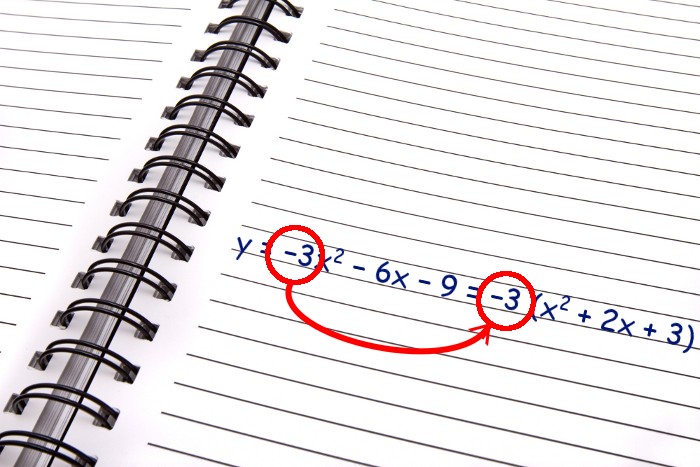Bewege den Koeffizienten außerhalb der Formel
Schritt 3: Vervollständige das Quadrat
Identifiziere den Koeffizienten von x in der modifizierten Gleichung. In dieser Gleichung ist es jetzt 2. Halbieren Sie den Koeffizienten und quadrieren Sie den Wert. Hier ist der resultierende Wert 1.
y=−3 (x2 + 2x + 3)
(2/2)2 =12=1
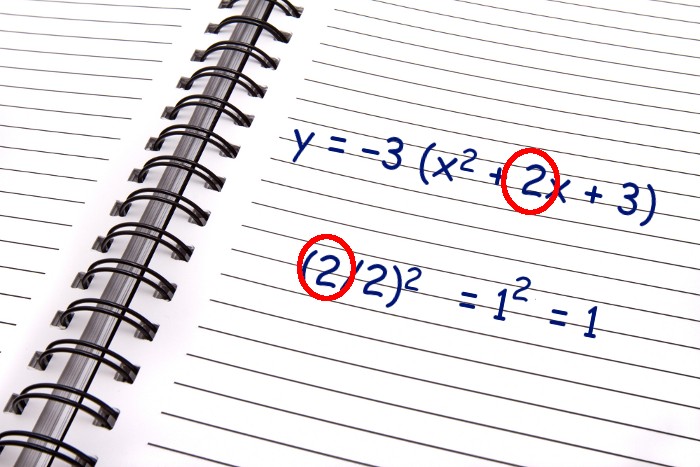Vervollständige das Quadrat
Schritt 4: Addieren und subtrahieren Sie den Wert aus Schritt 3 nach dem x in der Formel
Verschieben Sie Ihren Wert vom Vervollständigen des Quadrats in die Gleichung, die dem x-Wert in Ihrer Formel folgt.
y=−3 (x2 + 2x 1 – 1 + 3)
Addiere und subtrahiere den Wert aus Schritt 3 nach dem x in der Formel
Schritt 5: Faktorisiere die Gleichung
Faktorisierung ist einfach das Aufteilen der Gleichung in mehrere einfachere Faktoren. Hier verwenden wir das perfekte quadratische Trinom der ersten drei Terme.
y=−3 (x2 + 2x 1 – 1 + 3)
wird
y=−3 ((x+1)2 – 1 + 3)
Faktorisieren Sie die Gleichung
Schritt 6: Vereinfachen Sie die Formel erneut, um die Scheitelpunktform zu erhalten
Sie haben es fast geschafft. Jetzt muss die Formel nur noch weiter faktorisiert werden, bis Sie eine saubere Scheitelpunktgleichung erhalten.
y=−3 ((x+1)2 – 1 + 3)
Wird
y=-3 ((x+1)2 + 2)
Wird
y=-3(x+1)2 – 6
Dies ist die Scheitelpunktform der ursprünglichen Gleichung. Unten wird es im Scheitelpunktformat dargestellt:
y=a (x – h) 2 + k
Für dieses Beispiel ist die Gleichung h=-1 und k=-6
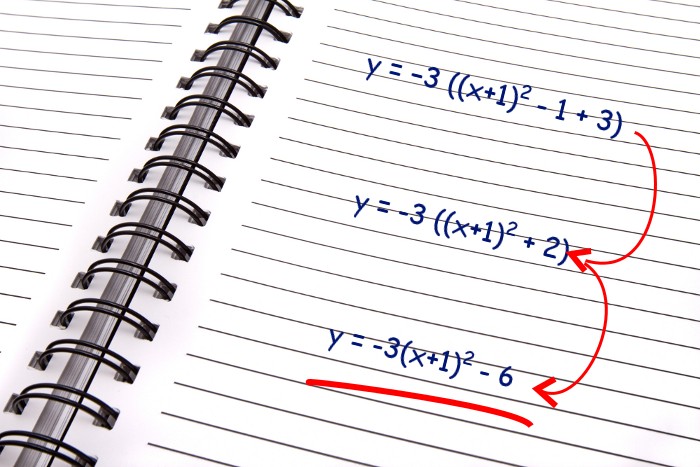Vereinfachen die Formel erneut, um die Scheitelpunktform zu erhalten
Sie können die Scheitelpunktformel verwenden, um Scheitelpunktkoordinaten zu identifizieren
Die Umwandlung quadratischer Gleichungen in die Scheitelpunktform ist eine Methode, um die Koordinaten des Scheitelpunkts der Kurve der Gleichung zu finden. Wenn Sie aus diesem Grund eine Standardgleichung in die Scheitelpunktform umwandeln, können Sie die Scheitelpunktkoordinaten (h und k) mit einer alternativen Methode ableiten. So geht’s:
Schritt 1: Nimm die Standardform einer Parabel und bestimme a, b und c
Hier ist die Standardform einer Parabel:
y=ax² + bx + c
Durch die Verwendung von a, b und see müssen Sie sich nicht mit einer Quadratwurzel befassen.
Nehmen Sie die Standardform einer Parabel und identifizieren Sie a, b und c
Schritt 2: Verwenden Sie die folgende Formel, um den h-Wert zu berechnen
Der h-Wert ist die x-Koordinate des Scheitelpunkts der Parabel. Sie können diesen Wert mit folgender Formel berechnen:
h=-b/(2a)
Für unsere Beispielformel: y=-3×2 – 6x – 9
a=-3, b=6 und c=9
Also,
h=6/(2 x-3)
Daher
h=-1
Verwenden Sie die nachstehende Formel, um den h-Wert zu berechnen
Schritt 3: Verwenden Sie die nachstehende Formel, um den k-Wert zu berechnen
Der h-Wert ist die x-Koordinate von der Scheitelpunkt der Parabel. Sie können diesen Wert mit folgender Formel berechnen:
k=c – b²/(4a)
Für unsere Beispielformel: y=-3×2 – 6x – 9
a=-3, b=6 und c=9
Also,
k=-9 – 6²/4(-3)
Daher
k=-6
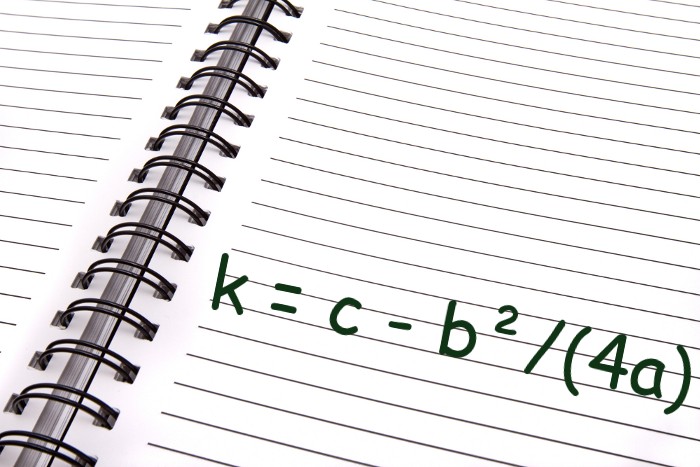Verwenden Sie die folgende Formel, um den k-Wert zu berechnen
Verwenden Sie einen Grafikrechner, um den Scheitelpunkt zu finden
Sie können einen Grafikrechner verwenden, um h zu ermitteln und k-Werte, die Sie dann verwenden können, um die Scheitelpunktform einer Gleichung darzustellen. Hier sind die grundlegenden Schritte zum Ermitteln des Scheitelpunkts auf einem Grafikrechner unter Verwendung der Beispielgleichung, die wir oben durchgearbeitet haben:
Schritt 1: Geben Sie die Gleichung in Ihren Grafikrechner ein
Sie können sie eingeben die Gleichung im Ausdrucksfeld. Möglicherweise müssen Sie die Ausdruckstaste drücken, die normalerweise ∱, ∱1 oder sogar enthält y=darauf. Geben Sie die Formel mit den Tasten auf der Tastatur Ihres Taschenrechners ein. Sobald Sie die Formel eingegeben haben, drücken Sie Enter.
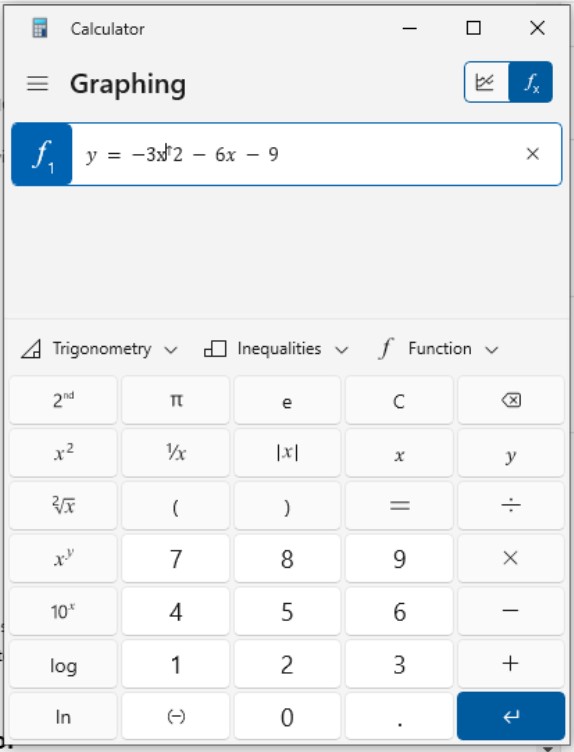Geben Sie die Gleichung in Ihren Grafikrechner ein
Schritt 2: Drücken Sie die Grafiktaste
Sobald Sie Ihre Gleichung eingegeben haben, drücken Sie die Grafiktaste oder das Symbol. Der Rechner generiert den Graphen der Gleichung. Die meisten Grafikrechner zeigen den Punkt an, an dem die Linie des Diagramms die y-Achse kreuzt, bekannt als y-Achsenabschnitt.
An diesem Punkt können Sie den Scheitelpunkt grafisch angezeigt sehen und seine Werte notieren.
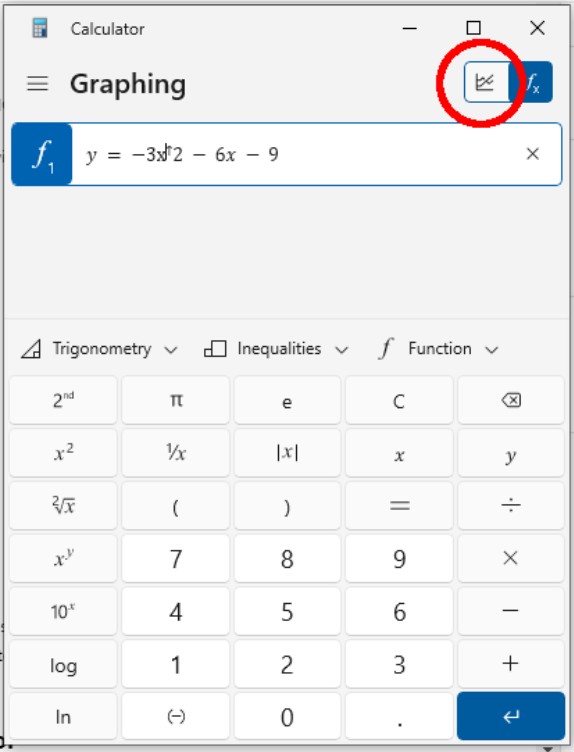Drücken Sie die Grafik-Schaltfläche 
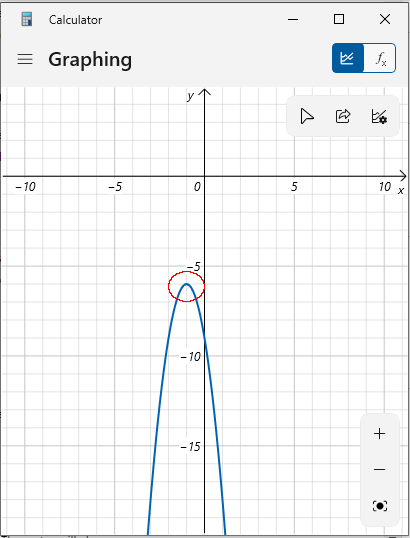An diesem Punkt können Sie den Scheitelpunkt grafisch angezeigt sehen und seine Werte notieren.
Schritt 3: Drücken Sie calc, um eine Funktionsanalyse zu erhalten
Das Herausfinden der Eigenschaften dieser Kurve wird uns mit den h-und k-Werten, die den Scheitelpunkt bestimmen, bewiesen. Drücken Sie die Schaltfläche calc oder analysis, um die Eigenschaften der Kurve anzuzeigen.
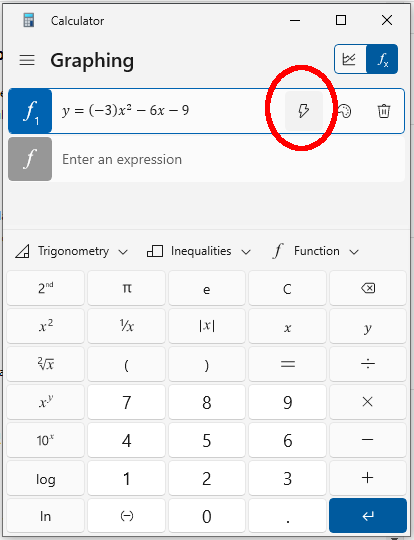Drücken Sie calc, um eine Funktionsanalyse zu erhalten
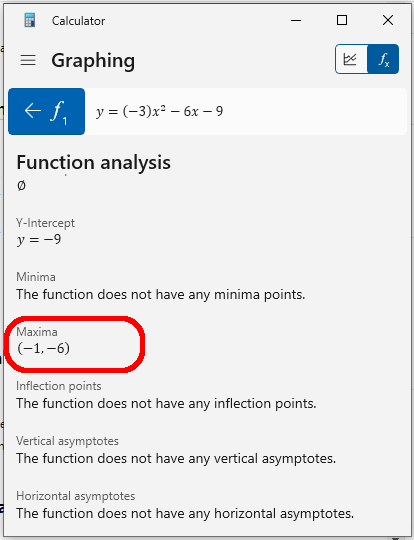
Schritt 4: Suchen Sie nach dem Maximum oder Minimum, um Ihre Scheitelwerte zu erhalten
Die Maxima-oder Minimapunkte sind die Punkte, an denen der Graph die Richtung ändert. Der Scheitelpunkt ist immer entweder ein Maximum oder ein Minimum der Gleichung, mit der Sie Ihren Taschenrechner programmiert haben.
Wie Sie sehen können, sind bei dieser Gleichung die h-und k-Werte eindeutig Maximapunkte. Das funktioniert bei jeder quadratischen Gleichung.
Suchen Sie nach dem Maximum oder Minimum, um Ihre Scheitelwerte zu erhalten
Wandeln Sie die Standardgleichung mit einem Online-Rechner in Scheitelpunkte um
Sie können den Notizblock und Taschenrechner umgehen und einen Online-Rechner verwenden leite die Scheitelpunktform deiner Gleichung ab. Es gibt viele Rechner online. So erhalten wir die Scheitelpunktform mit dem Taschenrechner unter Omni-Rechner:
Schritt eins: Nehmen Sie die a-, b-und c-Werte aus Ihrer Standardformel
In unserer ursprünglichen Gleichung y=-3×2 – 6x – 9
Also,
a=-3, b=-6 und c=-9
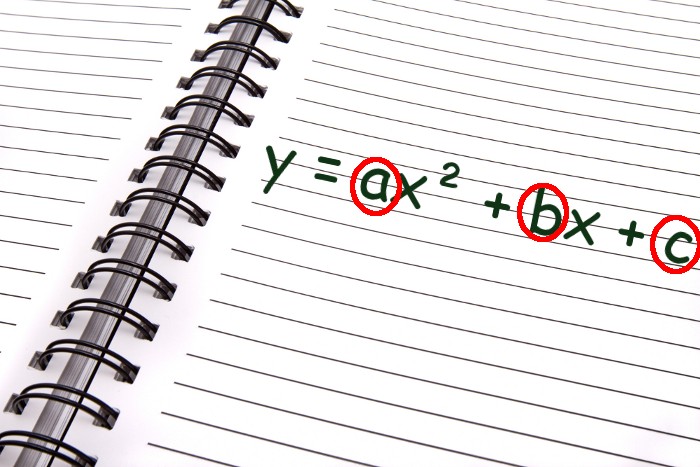Nehmen Sie die a-, b-und c-Werte aus Ihrer Standardformel
Schritt zwei: Geben Sie die a-, b-und c-Werte in die Felder von ein der Online-Rechner
Der Omni-Rechner zeichnet automatisch die Parabel und zeigt den Scheitelpunkt grafisch an.
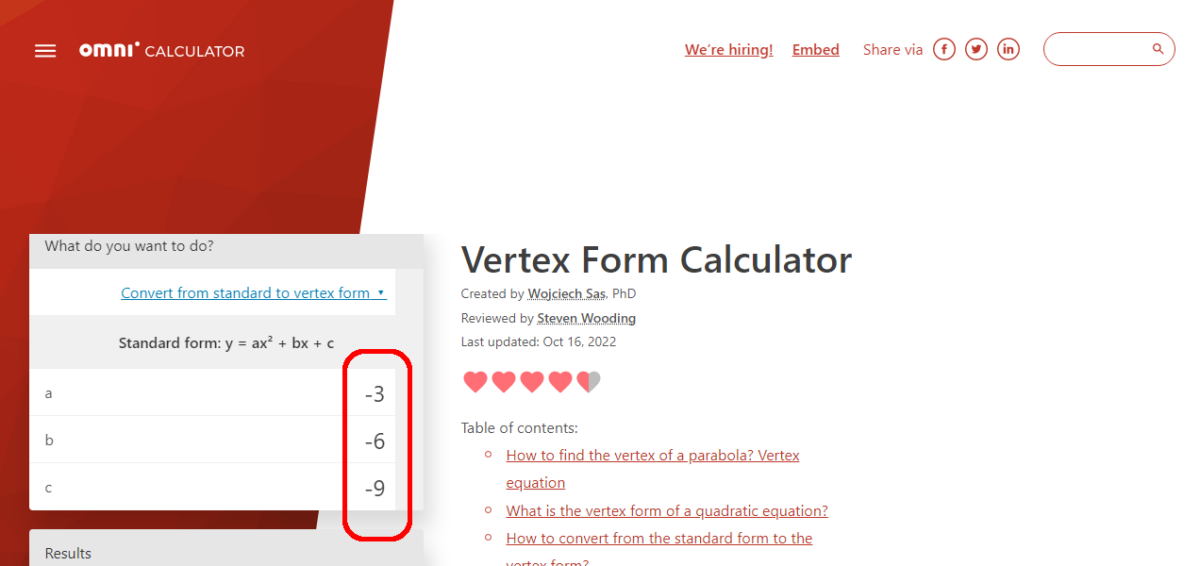Geben Sie die a-, b-und c-Werte in die Felder des Online-Rechners
unten ein die grafik, der rechner liefert die wichtigsten eigenschaften der parabel, ju st wie der Grafikrechner. Sie liefern die Standard-und Scheitelpunktformen der Gleichung zusammen mit dem Scheitelpunkt und dem Y-Achsenabschnitt. Dies funktioniert für jede quadratische Gleichung.
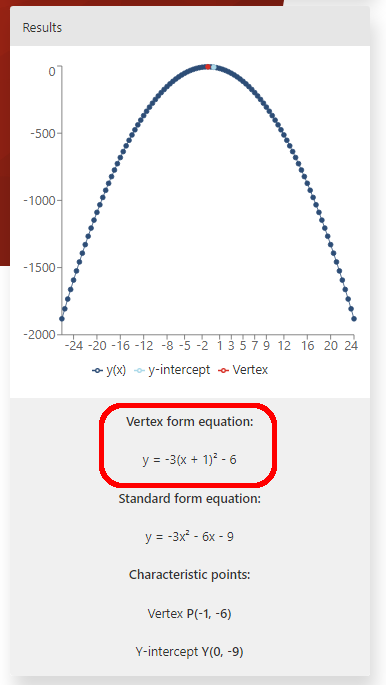Scrollen Sie nach unten, um die Scheitelpunktumwandlung Ihrer ursprünglichen Formel zu finden
Letzte Gedanken
Wie Sie sehen können, ist das Erhalten der Scheitelpunktform einer quadratischen Standardgleichung nicht so mysteriös wie Sie dachten. Indem Sie abwechselnd zwischen Standard-und Scheitelpunktgleichungen arbeiten, können Sie die Eigenschaften praktisch jeder Parabel definieren. Testen Sie diese Methoden mit Ihren eigenen Gleichungen und denken Sie daran, dass Übung den Meister macht!
Als Nächstes
FAQs (häufig gestellte Fragen) zum Konvertieren in Scheitelpunktform in einfachen Schritten
Was ist die Tangente einer Parabel?
Die Tangente einer Parabel ist eine Linie, die die Parabel an einem bestimmten Punkt schneidet.
Was ist die Normale einer Parabel?
Die Normale einer Parabel ist eine Linie, die im rechten Winkel zur Tangente der Parabel an ihrem Berührungspunkt gezogen wird.
Was ist die Leitlinie einer Parabel?
Die Leitlinie ist eine Linie, die immer im rechten Winkel zur Symmetrielinie der Kurve steht. Es berührt die Parabel nicht. Die Leitlinie hilft, die Parabel zu definieren.
Was ist die Exzentrizität einer Parabel?
Die Exzentrizität einer Parabel ist ein Verhältnis (nicht negative reelle Zahl), das für ihre Form spezifisch ist. Die Exzentrizität wird als Verhältnis des Abstands eines Punktes vom Brennpunkt der Parabel zum Abstand desselben Punktes von der Leitlinie der Parabel berechnet. Sie ist immer gleich 1.
Was ist eine Brennweite auf der Parabel?
Die Brennweite ist der Abstand eines identifizierten Punktes vom Brennpunkt. Er sollte dem Abstand des Punktes von der Leitlinie der Parabel entsprechen.