© Song_about_summer/Shutterstock.com
Beim Durchsuchen von Diagrammen oder Baumdatenstrukturen sind zwei beliebte Algorithmen die Tiefensuche (DFS) und die Breitensuche (BFS). Beide dienen dem gleichen Zweck, einen Pfad zu finden oder einen Graphen zu durchlaufen; DFS vs. BFS unterscheiden sich jedoch in Ansatz und Effizienz.
DFS ist rekursiv, traversiert tief in den Graphen hinein und geht zurück, wenn Sackgassen erreicht werden, während BFS iterativ alle benachbarten Knoten besucht, bevor es sich vorwärts bewegt. In diesem Artikel werden DFS und BFS gegenübergestellt, indem die wichtigsten Unterschiede sowie die Vor-und Nachteile der einzelnen Ansätze beschrieben werden.
DFS vs. BFS: Direkter Vergleich
DFS vs. BFS: Was ist der Unterschied?
Auf den ersten Blick Breitensuche (BFS) und Tiefensuche ( DFS)-Algorithmen scheinen ähnlich zu sein. BFS durchquert entsprechend der Baumbreite, während DFS der Tiefe folgt. Beide haben ein gemeinsames Ziel: das Durchsuchen von Graphen, um einen einzelnen Knoten oder Pfad zu lokalisieren. Daher werden die wichtigsten Unterschiede zwischen ihnen weiter unten besprochen.
Ansatz und Traversal-Reihenfolge
DFS (Depth First Search) und BFS (Breite First Search) sind zwei weit verbreitete Algorithmen zum Durchlaufen von Graphen und Bäumen. Beide Algorithmen besuchen jeden Knoten oder Scheitelpunkt des Graphen oder Baums; Die Reihenfolge der Durchquerung und Annäherung variiert jedoch.
DFS verfolgt einen Tiefen-Zuerst-Ansatz, bei dem jeder Zweig der Reihe nach durchquert wird, bis er die Tiefe eines jeden erreicht. Mit anderen Worten, es untersucht jeden Zweig so weit wie möglich, bevor es zurückverfolgt wird. Die von DFS verwendete Traversierungsreihenfolge ist LIFO (Last In First Out), was bedeutet, dass es eine Stack-Datenstruktur zum Speichern besuchter Knoten verwendet.
Umgekehrt verfolgt BFS einen Breiten-Zuerst-Ansatz; Es besucht alle Knoten in der aktuellen Tiefe, bevor es zu denen in einer tieferen Tiefe übergeht. Das heißt, es analysiert jeden Knoten auf jeder Ebene, bevor es weiter nach unten geht. Darüber hinaus ist seine Traversierungsreihenfolge FIFO (First In First Out), die eine Warteschlangendatenstruktur zum Speichern besuchter Knoten verwendet.
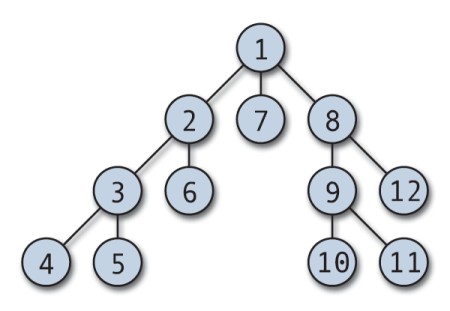Der DFS-Algorithmus durchsucht jeden Ast so weit wie möglich, bevor er zurückgeht.
©Wolfram Esser/CC BY-SA 3.0 – Lizenz
Zeitliche und räumliche Komplexität
Ein weiterer signifikanter Unterschied zwischen DFS und BFS ist ihre zeitliche und räumliche Komplexität. Die Zeitkomplexität von DFS ist O(V+E), wobei V die Anzahl der Scheitelpunkte und E die Kantenanzahl in einem Diagramm oder Baum ist. Darüber hinaus übersteigt seine Raumkomplexität auch O(V+E), da alle besuchten Knoten auf einem Stapel gespeichert werden müssen, bis sie ihre jeweiligen Blätter erreichen.
Im Gegensatz dazu hat BFS eine Zeitkomplexität von O(V+E) , ähnlich wie DFS; seine Platzkomplexität ist jedoch O(V), da es alle besuchten Knoten in einem Array speichert. Daher benötigt BFS möglicherweise mehr Speicher als DFS, wenn es um große Graphen oder Bäume geht.
Anwendungsfälle und Anwendungen
DFS und BFS haben unterschiedliche Verwendungen und Anwendungen. DFS wird häufig verwendet, wenn der Suchraum groß und tief ist, mit dem Ziel, einen bestimmten Pfad so weit zu erkunden, wie vor dem Zurückverfolgen. Es kann auch von Vorteil sein, wenn Sie versuchen, eine Lösung in Spielen oder Rätseln zu finden, bei denen die Antwort tief im Rätselraum liegen kann.
BFS hingegen wird häufig verwendet, wenn ein großes und flacher Suchraum, um den kürzesten Pfad zwischen zwei Knoten oder Scheitelpunkten zu identifizieren. Es bestimmt auch die kürzeste Entfernung zwischen zwei Netzwerkknoten oder Standorten auf einer geografischen Karte.
Vollständigkeit und Optimalität
Suchalgorithmen müssen zwei wesentliche Anforderungen erfüllen: Vollständigkeit und Optimalität. Vollständigkeit bezieht sich darauf, ob der Algorithmus garantieren kann, eine Lösung zu finden, falls eine existiert, während Optimalität bedeutet, den kürzesten oder optimalsten Weg zu dieser Lösung zu finden.
DFS ist nicht perfekt oder optimal, da es in einem stecken bleiben kann Endlosschleife oder nicht den kürzesten Weg finden. DFS könnte hängen bleiben, wenn ein Zyklus in seinem Diagramm oder Baum besuchte Knoten nicht verfolgt. Darüber hinaus kann DFS suboptimale Wege zur Lösung von Problemen finden.
BFS ist jedoch vollständig und optimal. Es garantiert, eine Lösung zu finden, falls eine existiert, sowie den kürzesten Weg darin zu finden. Nachdem alle Knoten auf einer Tiefenebene erkundet wurden, bevor zu einer anderen übergegangen wird, stellt BFS sicher, dass es den kürzesten Weg findet. Nichtsdestotrotz kann BFS in einigen Fällen länger dauern als DFS, besonders wenn es um tiefe oder schmale Graphen oder Bäume geht.
Speicherverwaltung
Ein weiterer entscheidender Faktor bei der Auswahl zwischen DFS und BFS ist der Speicher Management. Die Speicherverwaltung bezieht sich darauf, wie ein Algorithmus den Speicher verwendet und wie viel Platz zum Speichern besuchter Knoten erforderlich ist.
DFS verwendet einen Stack zum Speichern besuchter Knoten, aber große Suchräume oder Graphen können Probleme verursachen. In solchen Fällen kann DFS nicht genügend Arbeitsspeicher haben und keine optimale Lösung finden; dichte Graphen oder Bäume erfordern aufgrund häufiger Zyklen mehr Speicher.
BFS stützt sich auf eine Warteschlangen-Datenstruktur, um besuchte Knoten zu speichern, um sicherzustellen, dass ihm nicht der Speicher ausgeht. Unter bestimmten Umständen kann BFS jedoch mehr Speicher verwenden als DFS, insbesondere wenn der Graph oder Baum breit und flach ist oder viele Zweige hat. BFS könnte auch mehr Ressourcen benötigen, wenn es viele Knoten gibt oder die Struktur spärlich ist.
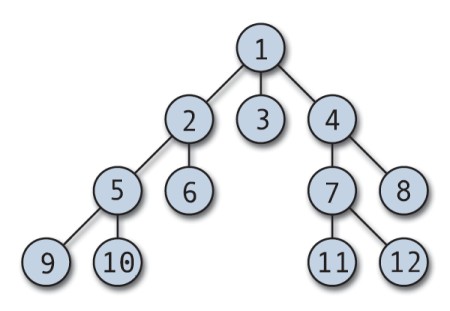Ein BFS-Algorithmus durchsucht alle Knoten in einer Tiefe, bevor er zu den Knoten in der nächsten Tiefe übergeht.
©Alexander Drichel/CC BY-SA 3.0 – Lizenz
Implementierungskomplexität
Die Implementierungskomplexität eines Algorithmus bezieht sich darauf, wie einfach oder schwierig es ist, ihn auszuführen. Dies hängt von der verwendeten Programmiersprache, den verfügbaren Datenstrukturen und der für einen erfolgreichen Abschluss erforderlichen Logik ab.
DFS ist normalerweise einfacher zu implementieren als BFS, da es nur eine Stack-Datenstruktur und eine rekursive Funktion oder Schleife benötigt. DFS kann mit einem einfachen Tiefensuchalgorithmus implementiert werden, der jeden Knoten besucht, bevor er nacheinander jeden Zweig untersucht. Außerdem ist es einfacher in rekursiven Programmiersprachen wie Python zu implementieren, wo Rekursion ganz natürlich ist.
BFS, on erfordert andererseits eine Warteschlangendatenstruktur und-schleife. Um es effizient zu implementieren, verwendet BFS einen Breitensuchalgorithmus, der alle Knoten in einer Tiefe besucht, bevor er zum nächsten übergeht. Die Implementierung von BFS in rekursiven Programmiersprachen wie Python kann jedoch schwieriger sein, da sie eine echte Schleife statt einer einfachen Rekursion erfordern.
Anwendungen
DFS und BFS haben unterschiedliche Anwendungen in verschiedenen Bereichen. DFS wird häufig in Computergrafik, künstlicher Intelligenz und Web-Crawling eingesetzt, um 3D-Modelle und-Bilder anzubieten, indem der 3D-Raum zum Rendern von Objekten untersucht wird. Künstliche Intelligenz verwendet DFS für Entscheidungsbäume oder Spielbäume – wobei jede mögliche Bewegung ausgewertet wird, um die Äste des Baums zu erkunden – während Webcrawler DFS verwenden, um das Web zu crawlen und Links auf Seiten zu erkunden.
BFS wurde in Netzwerken weit verbreitet Routing, Shortest-Path-Algorithmen und Rätsel. Beim Netzwerk-Routing findet es den kürzesten Pfad zwischen zwei Knoten, indem es alle möglichen Pfade untersucht, bis der kürzeste gefunden wird. BFS spielt auch eine Rolle in Shortest-Path-Algorithmen wie Dijkstra’s oder A*, die garantieren, die kürzeste Route zu finden; Ebenso können Sie beim Lösen von Rätseln wie Rubik’s Cube mit BFS die kürzeste Lösung bestimmen, die das Rätsel löst.
Die Verwendung von BFS zum Lösen von Rubik’s Cube bestimmt die schnellste Lösung zum Lösen des Puzzles.
©gd_project/Shutterstock.com
Suchraum
Der Suchraum ist die Menge aller möglichen Zustände oder Konfigurationen, die ein Algorithmus untersuchen kann, um seine Lösung zu finden. Es kann als Graph oder Baum dargestellt werden, wobei jeder Knoten einen Zustand oder eine Konfiguration darstellt und jede Kante einen Übergang zwischen ihnen darstellt.
DFS untersucht den Suchraum mit der Tiefe zuerst und untersucht jeden Zweig so weit wie möglich wie möglich, bevor Sie zurückgehen und andere Zweige erkunden. Dieser Ansatz funktioniert am besten für große und tiefe Suchräume, in denen die Lösung tief darin liegen kann. Unglücklicherweise kann DFS in einer Endlosschleife stecken bleiben, wenn eine Endlosschleife vorhanden ist und die besuchten Knoten nicht verfolgt.
BFS durchquert den Suchraum in der Breite zuerst und untersucht alle Knoten auf einmal Tiefe, bevor Sie mit dem nächsten fortfahren. Es ist ideal für große oder flache Suchräume, in denen die Lösung nahe an der Wurzel liegen kann. BFS garantiert, den kürzesten Weg zu dieser Lösung zu finden, kann aber in manchen Fällen mehr Speicherplatz beanspruchen und langsamer sein als DFS.
Suchstrategie
Eine Suchstrategie bezieht sich auf einen Algorithmus, der entscheidet, welcher Knoten als nächstes zu erkunden. Faktoren wie Kosten, Heuristik oder Zufälligkeit können diesen Entscheidungsprozess leiten.
DFS verwendet eine Tiefensuchstrategie, bei der jeder Zweig so weit wie möglich untersucht wird, bevor er zurückkehrt und andere Zweige untersucht. DFS verwendet keine Kosten oder Heuristiken bei der Auswahl des nächsten zu untersuchenden Knotens; daher kann es suboptimale Pfade erkunden. In bestimmten Fällen kann sich DFS auch auf Zufälligkeit verlassen, wie z. B. die Monte-Carlo-Baumsuche.
BFS verwendet normalerweise eine Breitensuchstrategie, bei der alle Knoten in einer Tiefe untersucht werden, bevor mit der nächsten fortgefahren wird. Umgekehrt verwendet es eine einheitliche Kostensuchstrategie, die Knoten mit den niedrigsten Kosten priorisiert. In bestimmten Fällen kann sich BFS auch auf Heuristiken wie den A*-Algorithmus stützen, der Kosten und geschätzte Entfernung verwendet, um zu entscheiden, welcher Knoten als nächstes erkundet werden soll.
DFS vs. BFS: 10 Fakten, die man kennen muss
DFS steht für Depth First Search, während BFS für Breadth First Search steht. DFS durchquert einen Graphen oder Baum in einer Tiefenbewegung, während BFS sich entsprechend der Baumbreite bewegt. Um die besuchten Knoten während der DFS-Durchquerung zu verfolgen, verwenden sie einen Stapel, während es bei BFS eine Warteschlange verwendet. während BFS darauf abzielt, den kürzesten Weg zwischen zwei Knoten zu finden. DFS benötigt weniger Platz, während BFS mehr benötigt, da es alle Knoten auf der aktuellen Ebene speichert, bevor es mit dem nächsten fortfährt. DFS ist schneller, wenn Probleme mit einer großen Anzahl von Knoten gelöst werden. während BFS sich im Umgang mit kleineren Gruppen auszeichnet. DFS durchläuft alle Knoten in einem Diagramm oder Baum, während BFS nur diejenigen auf dem kürzesten Weg besucht. DFS verwendet eine Tiefensuchstrategie, während BFS einen Breitenanfangsansatz verwendet. DFS kann dies nicht tun Finden Sie den kürzesten Weg, während BFS dies immer tut. Außerdem könnte DFS in einer Endlosschleife stecken bleiben, wenn Ihr Diagramm Zyklen enthält. BFS endet jedoch immer, wenn nur endliche Knoten übrig sind.
DFS vs. BFS: Welcher ist besser?
Depth-First Search (DFS) und Breadth-First Search (BFS) Algorithmen haben jeweils ihre eigenen spezifischen Vor-und Nachteile, wodurch sie besser geeignet sind bestimmte Szenarien als die anderen.
DFS durchquert effizient tiefe oder unendliche Graphen mit geringer Platzkomplexität und rekursionsbasierter Implementierung. Es erkennt auch effektiv Zyklen in einem Diagramm, da es jeden Zweig so weit untersucht, bevor es zurückverfolgt wird. DFS bietet Lösungen für Probleme wie das Auffinden zusammenhängender Komponenten, topologische Sortierung und das 8-Puzzle; Änderungen sind möglich.
Umgekehrt ist BFS besser geeignet, um den kürzesten Pfad zwischen zwei Knoten in einem Diagramm zu finden, da es alle Knoten in dieser Tiefe untersucht, bevor es zur nächsten Ebene übergeht. Darüber hinaus kann es verwendet werden, um den minimalen Spannbaum eines Graphen zu berechnen und Probleme wie Knight’s Tour zu lösen.
Beide Algorithmen haben ihre eigene Zeitkomplexität, und die Wahl zwischen ihnen hängt von dem jeweiligen Problem ab Eigenschaften des zu analysierenden Graphen. Im Allgemeinen hat BFS eine höhere Zeitkomplexität als DFS, garantiert jedoch den kürzesten Weg zwischen zwei Knoten in einem ungewichteten Graphen; Andererseits kann DFS eine geringere Komplexität aufweisen, garantiert aber nicht immer diesen kürzesten Weg.
Abschließend hängt die Wahl zwischen DFS und BFS von dem zu lösenden Problem und dem analysierten Diagramm ab. Beide Algorithmen haben ihre Stärken und Schwächen; Daher kann es hilfreich sein, beide zu verstehen, um die für ein bestimmtes Problem am besten geeignete auszuwählen. Es ist daher wichtig, beide Arten von Algorithmen in Ihrer Toolbox zu haben, zusammen mit Beispielen, in denen sie am vorteilhaftesten sind.
DFS vs. BFS: Vollständiger Vergleich und 9 Hauptunterschiede FAQs (häufig gestellte Fragen)
Welcher Algorithmus ist besser, um einen Pfad zwischen zwei Knoten zu finden?
BFS und DFS können verwendet werden, um einen Pfad zwischen zwei Knoten zu finden. BFS ist besser darin, die kürzeste Route zu finden, während DFS es vorzieht, Pfade zu finden, die vielleicht nicht die kürzesten sind, aber andere wünschenswerte Eigenschaften haben können, wie z. B. topologische Art oder stark verbundene Komponenten.
Welcher Algorithmus ist besser zum Durchlaufen eines spärlichen Graphen?
BFS eignet sich besser zum Durchlaufen eines spärlichen Graphen, da es alle Knoten auf einer Ebene untersucht, bevor es weitergeht, was es effizient macht, wenn es wenige Kanten gibt. Im Gegenteil, DFS kann viele unabhängige Knoten untersuchen, was es weniger effizient macht, wenn in spärlichen Diagrammen gearbeitet wird.
Welcher Algorithmus ist besser zum Durchlaufen eines dichten Diagramms?
DFS ist beim Durchlaufen eines dichten Graphen effizienter, da es Knoten in der Tiefe untersucht und schnell zu denjenigen zurückkehren kann, die für die Suche noch relevant sind. BFS kann jedoch viele irrelevante Knoten auf einmal prüfen, bevor es den gewünschten Knoten erreicht, was es in dichten Netzwerken weniger effektiv macht.
Können DFS und BFS verwendet werden, um die verbundenen Komponenten eines Diagramms zu finden?
Ja, sowohl DFS als auch BFS können verwendet werden, um die verbundenen Komponenten eines Graphen zu entdecken. DFS beginnt bei einem Knoten und durchquert es so weit wie möglich, bevor es zurückkehrt und andere nicht besuchte Knoten erkundet, während BFS alle Knoten auf einer Ebene untersucht, bevor es mit der nächsten fortfährt.
Können DFS und BFS verwendet werden? Zyklen in einem Diagramm erkennen?
Ja, sowohl DFS als auch BFS können verwendet werden, um Zyklen in Diagrammen zu erkennen. DFS erkennt Zyklen, indem es die besuchten Knoten in einer Liste und einem Stapel von untersuchten Knoten verfolgt; Wenn derselbe Knoten erneut erscheint, ohne in irgendeiner Reihenfolge sein übergeordneter Knoten zu sein, wird er als neuer Zyklus betrachtet. In ähnlicher Weise verwaltet BFS sowohl Listen besuchter Knoten als auch eine aktive Warteschlange von untersuchten Knoten; wenn ein zuvor besuchter Knoten wieder erscheint, ohne sein eigenes Kind in dieser letzteren Warteschlange zu sein, wird er als potenziell schädlich markiert.
Können DFS und BFS verwendet werden, um die topologische Art eines gerichteten azyklischen Graphen zu finden ( DAG)?
Ja, sowohl DFS als auch BFS können verwendet werden, um die topologische Art eines DAG zu bestimmen. Mit DFS geschieht dies, indem ein Index der besuchten Knoten sowie ein fortlaufender Stack der untersuchten Knoten verwaltet werden. Sobald alle Kinder jedes Knotens untersucht wurden, werden sie der topologischen Sortierung hinzugefügt; In ähnlicher Weise gibt es in BFS auch einen Index, der die besuchten Knoten zusammen mit einer fortlaufenden Warteschlange verfolgt, die auf die Erkundung wartet; Wenn alle Eltern eines Knotens untersucht wurden, wird er ebenfalls in die topologische Sortierung aufgenommen.
Können DFS und BFS verwendet werden, um den kürzesten Pfad in einem gewichteten Diagramm zu finden?
BFS kann verwendet werden, um den kürzesten Weg in einem ungewichteten Graphen zu finden, während der Dijkstra-Algorithmus für gewichtete Graphen verwendet wird. DFS kann jedoch auch erfolgreich sein, wenn Gewichtungen nicht negativ sind und die Suche auf eine verbundene Komponente beschränkt ist.