Es gibt viele Sortieralgorithmen, die zum Sortieren von Datensätzen verwendet werden können. Typischerweise werden diese Daten in einer Liste oder einem Array dargestellt. Von diesen Algorithmen ist der Auswahl-Sortier-Algorithmus einer der am einfachsten zu verstehenden und zu implementierenden. In diesem Artikel erklären wir die Theorie hinter Selection Sort, wie sie implementiert wird, und Best Practices für die Verwendung des Algorithmus.
Was ist Selection Sort?
Selection Sort ist ein vergleichsbasierter Sortieralgorithmus. Es funktioniert, indem das Array in zwei Teile geteilt wird – sortiert und unsortiert. Das Element mit dem kleinsten Wert wird ausgewählt und am Index 0 des sortierten Subarrays platziert. Das größte Element kann auch zuerst ausgewählt werden, je nachdem, ob Sie Ihre Liste aufsteigend oder absteigend sortieren möchten. Dies ist ein iterativer Prozess, dh die Methode wird wiederholt, bis alle Elemente an ihren richtigen Positionen in das sortierte Array eingefügt wurden. Wie zu erwarten, erhöht sich mit jeder Iteration die Größe des sortierten Subarrays um ein Element, während die Größe des unsortierten Arrays um ein Element abnimmt.
 Sie können die Auswahlsortierung mit einer Vielzahl von Programmiersprachen implementieren, darunter C, C++, C#, PHP, Java, Javascript und Python.
Sie können die Auswahlsortierung mit einer Vielzahl von Programmiersprachen implementieren, darunter C, C++, C#, PHP, Java, Javascript und Python.
Der Algorithmus hinter Selection Sort
Der Algorithmus hinter Selection Sort ist ziemlich einfach und folgt diesen Schritten:
 Das kleinste Element im unsortierten Array wird gefunden und mit dem ersten Element in Index 0 ausgetauscht. Das unsortierte Array ist dann durchlaufen, um das neue minimale Element zu finden. Wenn festgestellt wird, dass ein Element kleiner als das Element in Index 0 ist, werden die Elemente ausgetauscht. Das nächste minimale Element im unsortierten Array wird gefunden und dem sortierten Subarray gemäß der vorherigen Einschränkung hinzugefügt.Dieser Vorgang wird wiederholt, bis das gesamte Array sortiert ist.
Das kleinste Element im unsortierten Array wird gefunden und mit dem ersten Element in Index 0 ausgetauscht. Das unsortierte Array ist dann durchlaufen, um das neue minimale Element zu finden. Wenn festgestellt wird, dass ein Element kleiner als das Element in Index 0 ist, werden die Elemente ausgetauscht. Das nächste minimale Element im unsortierten Array wird gefunden und dem sortierten Subarray gemäß der vorherigen Einschränkung hinzugefügt.Dieser Vorgang wird wiederholt, bis das gesamte Array sortiert ist.
Funktionsweise von Selection Sort
Nun haben wir uns damit befasst, wie Selection Sort funktioniert, es ist Zeit, dies mit einem Beispiel zu veranschaulichen.
Wenn wir das Array [72, 61, 59, 47, 21]:
Der erste Durchlauf oder die Iteration des Prozesses beinhaltet das Durchlaufen des gesamten Arrays von Index 0 bis Index 4 (denken Sie daran, dass der erste Index auf 0 und nicht auf 1 gesetzt ist).
Das kleinste gefundene Element ist 21, also wird dieses mit dem ersten Element, 72, ausgetauscht. Dies ist unten dargestellt.
[21, 61, 59, 47, 72]
wo grün=sortiertes Element
Für den zweiten Durchgang finden wir 47 als zweitkleinsten Wert. Dieses wird dann mit 61 vertauscht.
[21, 47, 59, 61, 72]
Der dritte Durchgang erkennt 59 als drittes Element, das bereits in Position ist. Daher findet kein Austausch statt.
[21, 47, 59, 61, 72]
Der vierte Durchlauf findet 61 als viertes Element, das wiederum bereits vorhanden ist.
[21, 47, 59, 61, 72]
Der fünfte und letzte Durchlauf ergibt fast dasselbe. 72 ist das fünftkleinste oder größte Element und befindet sich an der richtigen Position. Jetzt ist das Array vollständig aufsteigend sortiert.
[21, 47, 59, 61, 72]
Implementierung von Selection Sort
Wir können implementieren Selection Sort mit einer Vielzahl von Programmiersprachen, darunter die gängigsten – C, C++, C#, PHP, Java, Javascript und Python. Zur Veranschaulichung verwenden wir Python. Der mit Python verwendete Code lautet wie folgt:
def SSort(arr, size): for step in range(size): min_idx=step for i in range(step + 1, size): if arr[i] arr [min_idx]: min_idx=i (arr[step], arr[min_idx])=(arr[min_idx], arr[step]) data=[-7, 39, 0, 14, 7] size=len(data) SSort(data, size) print(‘Ascending Sorted Array:’) print(data)
Erklärung des Codes
An dieser Stelle ist eine Erklärung des verwendeten Codes hilfreich. Zuerst definieren wir die Funktion „Sort“ als Funktion eines Arrays mit einer bestimmten Größe.
Die „for“-Schleife schreibt vor, dass eine Schleife beginnt, die über einen Bereich von „Größe“ iteriert die Länge des Arrays. Die „step“-Variable gibt an, dass jede Iteration die Werte 0, 1, 2… bis zu size-1 annehmen wird.
Die nächste Zeile zeigt, dass der Anfangswert von „step“ gleich der Variablen „ min_idx“. Dies ist eine Möglichkeit, die Position des kleinsten Elements im unsortierten Array zu verfolgen.
Die nächste „for“-Schleife gibt eine Schleife an, die über das unsortierte Array iteriert, beginnend bei „Schritt + 1“.. Dies liegt daran, dass das „Schritt“-Element bereits im sortierten Array platziert ist. Die „i“-Variable in jeder Iteration entspricht Schritt + 1, Schritt + 2 usw. bis zur Größe – 1.
Die „if“-Anweisung, die prüft, ob das aktuelle Element bei „i“ kleiner als das aktuelle Mindestelement ist. Wenn dies der Fall ist, wird das Minimum-Element aktualisiert, um dies widerzuspiegeln.
Zu guter Letzt hat diese ziemlich komplizierte Zeile eine einfache Bedeutung. Sobald die vorherige Schleife beendet ist, wird das kleinste unsortierte Element mit dem ersten Element im unsortierten Array ausgetauscht. Dadurch wird das Element effektiv am Ende des sortierten Arrays hinzugefügt.
Der Code unten gibt einfach das Array vor, mit dem wir arbeiten, mit der Länge „Größe“, und ruft Selection Sort auf, um daran zu arbeiten Reihe. Die Ausgabe wird dann mit dem Titel „Ascending Sorted Array“ gedruckt.
Wann immer Sie Python verwenden, ist es wichtig, dass Sie die richtige Einrückung verwenden, um die einzelnen Operationen zu bezeichnen. Andernfalls erhalten Sie eine Fehlermeldung und die Berechnung wird nicht ausgeführt.
Wie der Code aussieht
Schauen Sie sich den Screenshot unten an, um zu sehen, wie dieser Code aussieht, wenn er darin implementiert ist Python.
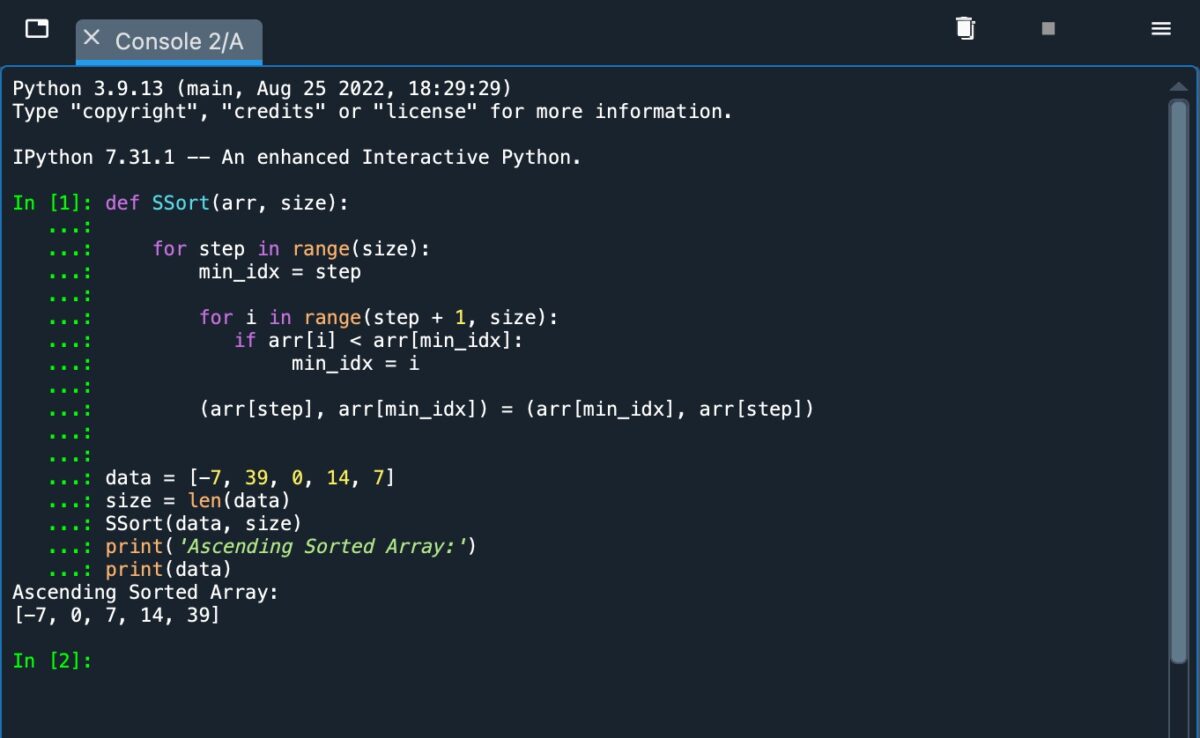 Bei Verwendung Python müssen Sie die richtige Einrückung verwenden, um die einzelnen Operationen zu bezeichnen.
Bei Verwendung Python müssen Sie die richtige Einrückung verwenden, um die einzelnen Operationen zu bezeichnen.
©”TNGD”.com
Beste und schlechteste Anwendungsfälle von Insertion Sort
Während Insertion Sort nützlich ist Für viele Zwecke hat es, wie bei jedem Algorithmus, seine besten und schlechtesten Fälle. Dies liegt hauptsächlich an der Zeit-und Platzkomplexität.
Zeitkomplexität mit Insertion Sort
Die Zeitkomplexität kann in jedem Fall in der folgenden Tabelle beschrieben werden:
Like Bei jedem Algorithmus hat die Auswahlsortierung ihre eigene zeitliche und räumliche Komplexität. Dies bezieht sich im Wesentlichen darauf, wie sich die Komplexität oder Geschwindigkeit der Ausführung in einer Vielzahl von Fällen ändert. Die Zeitkomplexität kann wie in der folgenden Tabelle zusammengefasst werden:
Der beste Fall bezieht sich darauf, wenn das Array sortiert ist, Der durchschnittliche Fall bezieht sich darauf, wenn das Array durcheinander ist, und der schlimmste Fall bezieht sich darauf, wenn das Array entweder in aufsteigender oder absteigender Reihenfolge ist und Sie die entgegengesetzte Reihenfolge wünschen. Mit anderen Worten, sie beziehen sich darauf, wie viele Iterationen erforderlich sind, um den Prozess abzuschließen, wobei im schlimmsten Fall die maximale Anzahl von Iterationen erforderlich ist.
In diesem Fall ist die Zeitkomplexität für die Auswahlsortierung in allen identisch Fall. Dies liegt daran, dass der Algorithmus immer die gleiche Anzahl von Vergleichen und Vertauschungen durchführt, egal wie sortiert das Array ist. Daher ist die Komplexität O(n2), auch bekannt als quadratische Zeit. Dies ist einer der Hauptgründe, warum der Algorithmus im Vergleich zu Sortieralgorithmen nicht sehr effizient ist, aber es bedeutet auch, dass die Effizienz nicht von der Verteilung der Eingabe abhängt.
Space Complexity with Selection Sort
Die Raumkomplexität bezieht sich darauf, wie viel Speicher für die Berechnungen benötigt wird. Im Falle einer Auswahlsortierung ist dies gleich O(1). Dies bedeutet, dass unabhängig von der Eingabegröße eine konstante Menge an Speicher benötigt wird. Die einzige temporäre Variable, die gespeichert wird, ist „min_idx“, die sich mit zunehmender Eingabegröße nicht ändert.
Zusammenfassung
Auswahlsortierung ist ein relativ einfacher, aber ziemlich ineffizienter Algorithmus zum Sortieren von Elementen in einer gegebenen Eingabe. Es ist vor allem für sehr kleine Datensätze geeignet und kann mit einer Vielzahl von Programmiersprachen implementiert werden. Auswahlsortierung funktioniert, indem das Array in zwei Subarrays aufgeteilt wird, sortiert und unsortiert. Der Prozess durchläuft dann ein Array, um das minimale Element zu finden, und verschiebt dieses Element auf den Index 0. Der Prozess wird wiederholt, wobei die zweit-und drittkleinsten Elemente usw. gefunden und an ihre korrekten Indexpositionen ausgetauscht werden. Dies wird fortgesetzt, bis das gesamte Array sortiert ist.
Als Nächstes …
Auswahl-Sortieralgorithmus erklärt, mit Beispielen FAQs (häufig gestellte Fragen)
Was ist selection sort?
Selection sort ist ein einfacher Sortieralgorithmus, der ein Array von Elementen entweder in aufsteigender oder absteigender Reihenfolge sortiert. Dazu wird das Array durchlaufen, um das kleinste Element zu finden, und dieses mit dem Element in Index 0 in einem sortierten Unterarray ausgetauscht. Das unsortierte Subarray wird dann erneut durchlaufen, und das minimale Element wird gefunden und in seine richtige Position getauscht. Der Algorithmus wiederholt diesen Vorgang, bis das gesamte Array sortiert ist. Selection Sort ist ein einfacher Sortieralgorithmus, der wiederholt das kleinste Element aus einem unsortierten Teil des Arrays findet und es am Anfang des sortierten Teils des Arrays platziert. Der Algorithmus behält zwei Subarrays in einem gegebenen Array bei.
Was sind die Vorteile von Selection Sort?
Selection Sort ist ein sehr einfach zu verstehender und zu implementierender Algorithmus , und reicht für sehr kleine Datensätze aus.
Welche Nachteile hat die Auswahlsortierung?
Da sie nicht sehr effizient ist, ist die Auswahlsortierung unzureichend Umgang mit großen Datensätzen. Seine Effizienz hängt nicht von der Verteilung der Eingabe ab, aber das bedeutet auch, dass es in allen Fällen ineffizient ist, egal wie sortiert das anfängliche Array bereits ist. Es ist auch kein stabiler Algorithmus, was bedeutet, dass die relative Reihenfolge gleicher Elemente möglicherweise nicht erhalten bleibt. Alles in allem gibt es für die meisten Fälle überlegene Sortieralgorithmen, die sich besser an die jeweilige Eingabe anpassen können.
In welchen Situationen eignet sich die Auswahlsortierung am besten?
Auswahlsortierung wird am besten verwendet, wenn die Eingabegröße klein ist und Sie eine einfache und relativ effiziente Lösung suchen. Da die Platzkomplexität O(1) ist, hat Selectionsort Vorteile, wenn Sie die Speichernutzung im Auge behalten müssen. Da es immer die gleiche Anzahl von Iterationen durchführt, kann es beim Sortieren eines Arrays, das bereits teilweise sortiert ist, besser abschneiden als einige andere Algorithmen, da es besser ist, die gleiche Zeit zu benötigen als länger. Wenn Sie keinen stabilen Sortieralgorithmus benötigen, ist Selection Sort eine gute Wahl.
Wie hoch ist die zeitliche Komplexität von Selection Sort?
Die Zeit Die Komplexität der Auswahlsortierung ist quadratisch, dargestellt als O(n2).
Was ist die Raumkomplexität der Auswahlsortierung?
Die Raumkomplexität ist O( 1). Dies bedeutet, dass für jede Iteration eine konstante Speichermenge verwendet wird, da nur eine temporäre Variable gespeichert werden muss. Obwohl der Algorithmus ineffizient sein kann, bedeutet die Platzkomplexität, dass er Vorteile in Situationen hat, in denen die Speichernutzung eingeschränkt ist.
Welche Alternativen zur Auswahlsortierung gibt es?
Viele andere Sortieralgorithmen sind in den meisten Anwendungsfällen effizienter. Dazu gehören Merge-Sort, Quick-Sort und Heap-Sort. Diese Algorithmen neigen dazu, anpassungsfähiger zu sein und haben eine viel bessere Zeitkomplexität. Von diesen Alternativen ist Mergesort der einzige stabile Algorithmus, daher ist er praktikabel, wenn Sie die relative Reihenfolge gleicher Elemente beibehalten müssen.
Ist Selection Sort ein stabiler Algorithmus?
Nein, es ist kein stabiler Algorithmus. Das bedeutet, dass beim Sortieren eines Arrays Elemente mit gleichem Wert nach dem Austausch möglicherweise nicht in ihrer ursprünglichen Reihenfolge erhalten bleiben.