© BEST-BACKGROUNDS/Shutterstock.com
Es gibt viele Anwendungen für verknüpfte Listen, beispielsweise in der Musik-und Bildverarbeitung und der Darstellung von Graphen, Bäumen und komplizierteren Datenstrukturen. Aber warum sollten Sie eine verkettete Liste umkehren wollen? Lassen Sie uns darauf eingehen.
Was ist eine umgekehrte verkettete Liste?
Wie Sie wahrscheinlich erraten können, ist es eine verkettete Liste, die… umgekehrt wurde! Normalerweise zeigt jeder Knoten auf den nächsten Knoten in einer Liste, beginnend mit dem Kopfknoten und endend mit dem Schwanzknoten. Wenn Sie jedoch eine verknüpfte Liste umkehren, werden die Zeiger umgekehrt, sodass der Kopf zum Schwanz und der Schwanz zum Kopf wird. Betrachten Sie den einfachen Fall einer 5-Knoten-Liste. Dies würde normalerweise so aussehen:
Kopf → Knoten1 → Knoten2 → Knoten3 → Knoten4 → Knoten5 → Schwanz
Sobald wir die Liste umkehren, erhalten wir:
Schwanz → node5 → node4 → node3 → node2 → node1 → head
Auch wenn die Liste länger wird und mehr Datenwerte enthält, bleibt das Prinzip gleich.
Warum würden Sie umkehren wollen a Verkettete Liste?
Da eine umgekehrt verkettete Liste immer noch eine verkettete Liste ist, sind viele Anwendungen ähnlich. Als solche werden umgekehrte Listen immer noch beim Implementieren weiterer Datenstrukturen in Stapeln und in Warteschlangen verwendet. Aber es gibt einige einzigartige Verwendungen, die umgekehrt verknüpfte Listen auf den Tisch bringen:
Da die Elemente umgekehrt sind, können wir die Elemente drucken und die Liste in umgekehrter Reihenfolge verarbeiten. Dies ist hilfreich, wenn Sie den Internetverlauf eines Browsers anzeigen möchten. Wenn Sie einige Elemente am Ende der Liste löschen möchten, macht die Umkehrung dies viel einfacher. Dies liegt daran, dass diese Elemente jetzt am Anfang der Liste stehen. Dies kann viel Zeit sparen, insbesondere wenn die Liste sehr umfangreich ist. Sie müssen nicht die gesamte Liste durchlaufen, wenn Sie die Liste umkehren. Manchmal möchten wir einen rekursiven Algorithmus auf einer gesamten Liste ausführen und Operationen an jedem Knoten ausführen. In einigen dieser Fälle kann es sinnvoller sein, sie in umgekehrter Reihenfolge zu verarbeiten. Ein weiterer Grund, eine umgekehrt verknüpfte Liste zu verwenden, besteht darin, zu überprüfen, ob die Liste palindromisch ist – das bedeutet, dass die Reihenfolge vorwärts oder rückwärts gleich ist. Ein Beispiel hierfür wäre die Zahl 212. Wie man es auch betrachtet, die Abfolge der Datenwerte ist identisch.
Wie man eine verknüpfte Liste umkehrt
Es gibt im Allgemeinen zwei Ansätze, um eine verknüpfte Liste umzukehren – den iterativen Ansatz und den rekursiven Ansatz. Schauen wir uns diese an.
Der iterative Ansatz
Bei dieser Methode wiederholen wir die Ausführung des Algorithmus, bis jeder Zeiger umgekehrt wurde. Wir tun dies, indem wir unsere Knoten mit den Attributen „prev“, „curr“ und „next“ verfolgen. Wir können diese wie folgt zuweisen:
while (current !=NULL) { next=current-> next current-> next=prev prev=current current=next } head_ref=prev
Die „while“-Anweisung im Grunde iteriert über jeden Knoten, der nicht null ist.
Die nächste Zeile verfolgt den nächsten Knoten in der Liste, damit wir ihn nicht verlieren, wenn wir die Zeiger umkehren.
Dann setzen wir das „next“-Attribut des aktuellen Knotens auf den vorherigen Knoten und kehren die Zeiger um.
Die nächste Zeile setzt das „prev“-Attribut auf den vorherigen Knoten und verfolgt es wie wir den nächsten Knoten.
Die vorletzte Zeile besagt, dass der „aktuelle“ Zeiger auf dem nächsten Knoten ist, sodass wir uns iterativ entlang der Liste bewegen können.
Zuletzt setzen wir die „head_ref ” Zeiger auf den letzten Knoten der ursprünglichen Liste, der der erste Knoten in der umgekehrten Liste sein wird. Daher setzen wir dies als neuen Hauptknoten.
So können wir diesen Prozess in Python implementieren:
class Node: def __init__(self, data): self.data=data self. next=None class LinkedList: def __init__(self): self.head=None def push(self, new_data): new_node=Node(new_data) new_node.next=self.head self.head=new_node def reverse(self): prev_node=Keine aktueller_Knoten=self.head, während aktueller_Knoten nicht Keine ist: next_node=aktueller_Knoten.next aktueller_Knoten.next=vorheriger_Knoten prev_node=aktueller_Knoten aktueller_Knoten=next_node self.head=vorheriger_Knoten def printList(self): aktueller_Knoten=self.head while aktueller_Knoten: print( current_node.data, end=””) current_node=current_node.next my_list=LinkedList() my_list.push(16) my_list.push(2) my_list.push(19) my_list.push(71) print(“Gegebene verknüpfte Liste”) meine_liste.printList() meine_liste.reverse () print(“\nUmgekehrte verkettete Liste”) my_list.printList()
Zunächst definieren wir die Klassen „Node“ und „LinkedList“. Dann definieren wir die „Push“-Funktion, die verwendet wird, um einen neuen Knoten am Anfang der Liste hinzuzufügen, der als Kopfknoten bezeichnet wird.
Dann sehen wir die implementierte „Reverse“-Funktion ganz ähnlich wie zuvor beschrieben.
Schließlich definieren wir die „printList“-Funktion für die „LinkedList“-Klasse, die den Datenwert an jedem Knoten druckt, was bis zum „current_node “ ist gleich „None“, was anzeigt, dass wir das Ende der Liste erreicht haben. Sehen Sie sich den Screenshot an, um zu sehen, wie dies in Python funktioniert.
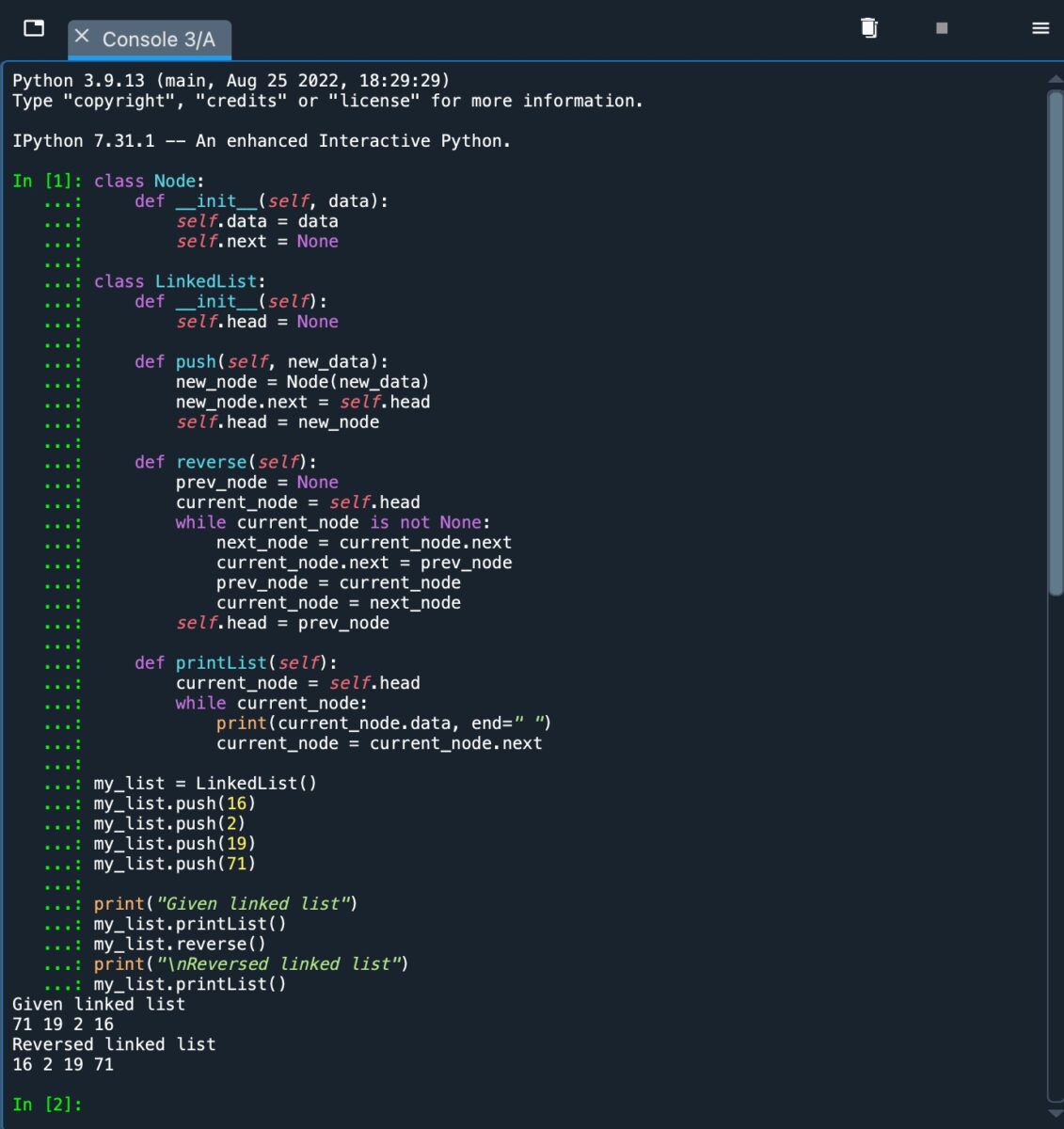Der iterative Ansatz zum Umkehren einer verketteten Liste, implementiert in Python.
©”TNGD”.com
Der rekursive Ansatz
Die andere Methode zum Umkehren eine verkettete Liste ist der rekursive Ansatz. Während iterative Ansätze mit Schleifen oder sich wiederholenden Anweisungen arbeiten, um ein Problem zu lösen, führen rekursive Ansätze dieselbe Funktion an immer kleineren Beispielen desselben Problems aus. Sobald diese Teilprobleme gelöst sind, werden die Lösungen kombiniert, um ein Gesamtergebnis für das Ausgangsproblem zu ergeben. Mal sehen, wie die Rekursion zum Umkehren einer verketteten Liste funktioniert:
Zuerst teilen wir die Liste in zwei Teile, den ersten Knoten und die verbleibende Liste.
Dann nennen wir die „ reverse”-Funktion für die verbleibende Liste.
Diese umgekehrte Liste wird dann mit dem ersten Knoten verknüpft, und der ursprüngliche Kopfzeiger wird auf NULL gesetzt. Der neue Head-Zeiger wird auf den neuen Head-Knoten gesetzt und die Liste wird umgekehrt.
Hier sehen Sie, wie dies implementiert wird:
class Node: def__init__(self, data): self. data=data self.next=None class LinkedList: def__init__(self): self.head=None def push(self, new_data): new_node=Node(new_data) new_node.next=self.head self.head=new_node def reverse_recursive( self, current_node): wenn current_node None oder current_node.next None ist: return current_node rest=self.reverse_recursive(current_node.next) current_node.next.next=current_node current_node.next=None return rest def reverse(self): self. head=self.reverse_recursive(self.head) def printList(self): aktueller_Knoten=self.head while aktueller_Knoten: print(aktueller_Knoten.data, end=””) aktueller_Knoten=aktueller_Knoten.next print() meine_Liste=LinkedList() meine_Liste. push(16) meine_liste.push(2) meine_liste.push(19) meine _list.push(71) print(“Gegebene verknüpfte Liste”) my_list.printList() my_list.reverse() print(“Umgekehrte verknüpfte Liste (rekursiv):”) my_list.printList()
Ein Großteil dieses Codes ist das gleiche wie der iterative Prozess. Der Hauptunterschied liegt wenig überraschend in der verwendeten Reverse-Funktion.
In diesem Fall definieren wir die Funktion „reverse_recursive“ als Funktion des aktuellen Knotens. Jeder Knoten danach wird rekursiv umgekehrt, indem die Umkehrfunktion mit dem nächsten Knoten als Eingabe aufgerufen wird, bis der aktuelle Knoten gleich „None“ ist. Dies geschieht, wenn das Ende der Liste erreicht ist, oder in dem einfachen Fall, in dem es nur einen Knoten in der Liste gibt.
Dann wird der aktuelle Knoten umgekehrt, indem das „next“-Attribut des nächsten Knotens aktualisiert wird auf den aktuellen Knoten und das „next“-Attribut des aktuellen Knotens auf „None“. Der aktuelle Knoten wird zum Ende der umgekehrten Liste.
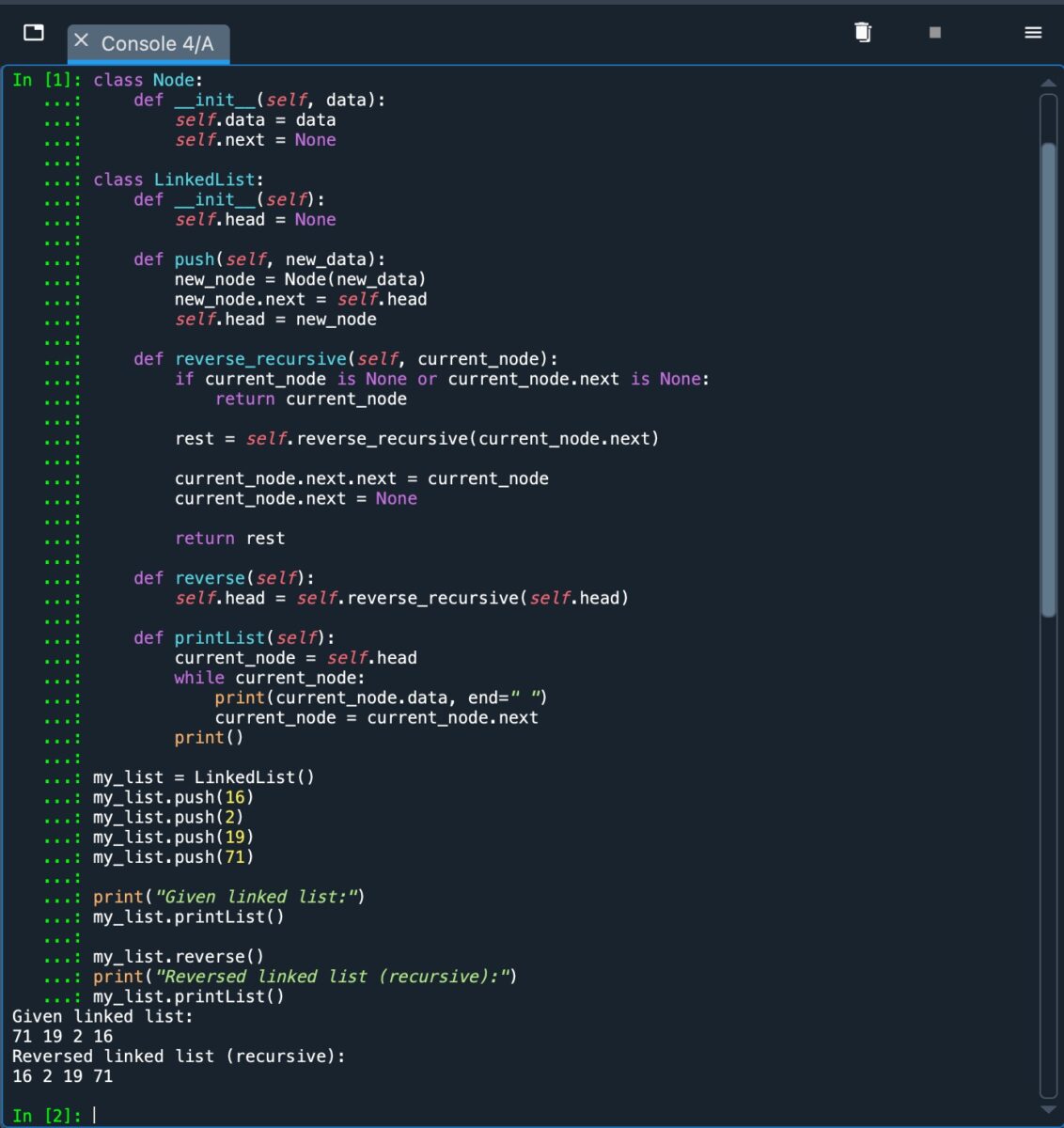Der rekursive Ansatz zum Umkehren einer verketteten Liste, implementiert in Python.
©”TNGD”.com
Zusammenfassung
Wenn Sie umkehren müssen B. einer verketteten Liste, können Sie zwischen einem iterativen und einem rekursiven Ansatz wählen. Während iterative Ansätze auf der Wiederholung derselben Anweisungen in einer „while“-Schleife für jeden Knoten beruhen, führen rekursive Funktionen ihre Funktion auf kleineren Instanzen desselben Problems aus. Das Umkehren einer verknüpften Liste kann nützlich sein, um die Palindromizität einer Liste zu erkennen und Elemente am Ende der ursprünglichen Liste zu ändern.
Wie man eine verknüpfte Liste umkehrt, mit Beispielen FAQs (häufig gestellte Fragen)
Was ist eine umgekehrte verkettete Liste?
Eine umgekehrte verkettete Liste ist eine verkettete Liste, bei der die Reihenfolge ihrer Elemente umgekehrt wurde, sodass der letzte Knoten zum ersten wird Knoten der neuen Liste, und die Zeiger werden umgekehrt.
Warum sollten Sie eine verknüpfte Liste umkehren?
Das Umkehren einer Liste kann nützlich sein feststellen, ob eine Liste palindromisch ist, Elemente am Ende der ursprünglichen Liste ändern (wie sie jetzt am Anfang stehen) oder wenn Sie bestimmte Algorithmen verwenden möchten, die besser mit einer umgekehrten Liste zu verwenden sind.
Wie können Sie eine verkettete Liste umkehren?
Die gebräuchlichsten Möglichkeiten, eine verkettete Liste umzukehren, sind iterative oder rekursive Funktionen. Während der iterative Ansatz funktioniert, indem er die Liste durchläuft und die Zeiger jedes Knotens ändert, funktioniert die rekursive Umkehrfunktion, indem sie die Liste bis auf den Kopfknoten umkehrt und dann die Zeiger des aktuellen Knotens aktualisiert.
Wie Kehren Sie doppelt verknüpfte Listen und kreisförmig verknüpfte Listen um?
Sie können eine doppelt verknüpfte Liste auf die gleiche Weise wie eine einfach verknüpfte Liste umkehren, aber Sie müssen das „nächste“ und aktualisieren „prev“-Attribute jedes Knotens entsprechend. Bei zirkulär verknüpften Listen müssen Sie das „next“-Attribut des Endknotens aktualisieren, damit es auf den neuen Kopfknoten zeigt.
Wie hoch ist der zeitliche Aufwand für die Umkehrung einer verknüpften Liste?
Die Zeitkomplexität ist gleich O(n), wobei n die Anzahl der Knoten ist, da Sie die Liste durchlaufen müssen, um die Zeiger umzukehren, egal welche Methode Sie verwenden.
Was ist die Raumkomplexität beim Umkehren einer verknüpften Liste?
Die Raumkomplexität ist gleich O(1) bezüglich des iterativen Ansatzes, da die temporären Variablen, die Sie zum Umkehren der Liste benötigen, bestehen bleiben Konstante. Beim rekursiven Ansatz ist die Platzkomplexität gleich O(n), da Sie jeden Aufruf der rekursiven Funktion in einem Stack speichern müssen.