© TippaPatt/Shutterstock.com
Informatiker verwenden oft Graphen, um Daten darzustellen. Graphen können verschiedene Beziehungen darstellen, von Karten und chemischen Verbindungen bis hin zu sozialen Beziehungen und Computernetzwerken. Wir können viele Algorithmen mit Graphen verwenden, wie zum Beispiel den Dijkstra-Algorithmus, die Depth-First Search (DFS)-Algorithmus und den Breadth-First Search (oder BFS)-Algorithmus. Während Sie beide Algorithmen verwenden können, um die Knoten eines Graphen zu durchlaufen, ist BFS besser für ungewichtete Graphen. In diesem Artikel werden wir untersuchen, wie BFS funktioniert und welche Anwendungen es gibt.
Was ist BFS?
BFS ist ein Suchalgorithmus. Der Algorithmus beginnt seine Traversierung am Quellknoten und besucht dann die Nachbarknoten. Danach wählt der Algorithmus den nächstgelegenen Knoten auf der nächsten Tiefenebene aus und besucht dann die unerforschten Knoten daneben und so weiter. Da der BFS-Algorithmus die Knoten auf jeder Ebene besucht, bevor er zur nächsten Ebene übergeht, kommt der Name „Breite zuerst“ daher. Wir stellen sicher, dass wir jeden Knoten nur einmal besuchen, indem wir besuchte und nicht besuchte Knoten nachverfolgen. Sie können BFS verwenden, um Pfadentfernungen zu berechnen, genau wie mit dem Algorithmus von Dijkstra. scaled.jpg” height=”1709″width=”2560″>
Der Algorithmus hinter BFS
Wir können den grundlegenden Algorithmus mit dem folgenden Pseudocode darstellen:
BFS(graph, start): queue=[start] visited=set(start) while queue is not empty: node=dequeue(queue) process(node) für Nachbar in graph.neighbors(node): wenn Nachbar nicht in visited: visited.add(neighbor) enqueue(queue, Neighbor)
In diesem Fall definieren wir einen Graphen als „Graph“, und „Start“ ist der Startknoten.
Wir implementieren eine Warteschlangenstruktur, um die nicht besuchten Knoten zu halten , sowie eine „besuchte“ Menge, um die besuchten Knoten zu halten.
Die „while“-Schleife wird fortgesetzt, bis die Warteschlange leer ist, und initiiert die Verarbeitung der Knoten Ebene für Ebene. Die „dequeue“-Funktion entfernt den ersten Knoten aus der Warteschlange, während er besucht wird.
Die „process“-Funktion führt eine gewünschte Funktion auf dem Knoten aus, wie z. B. das Aktualisieren der Entfernung zu seinen Nachbarn oder das Drucken von Daten zu der Konsole.
Die „for“-Schleife durchläuft alle Nachbarn des aktuellen Knotens und prüft, ob der Knoten bereits besucht wurde. Wenn nicht, wird es mit der Funktion „enqueue“ in die Warteschlange eingefügt. Im Wesentlichen werden die Knoten auf jeder Ebene in der Warteschlange gespeichert, wobei ihre Nachbarn hinzugefügt werden, um auf der nächsten Tiefenebene besucht zu werden. Dadurch können wir den kürzesten Pfad zwischen dem Quellknoten und jedem anderen Knoten im Diagramm bestimmen.
Die Funktionsweise von BFS
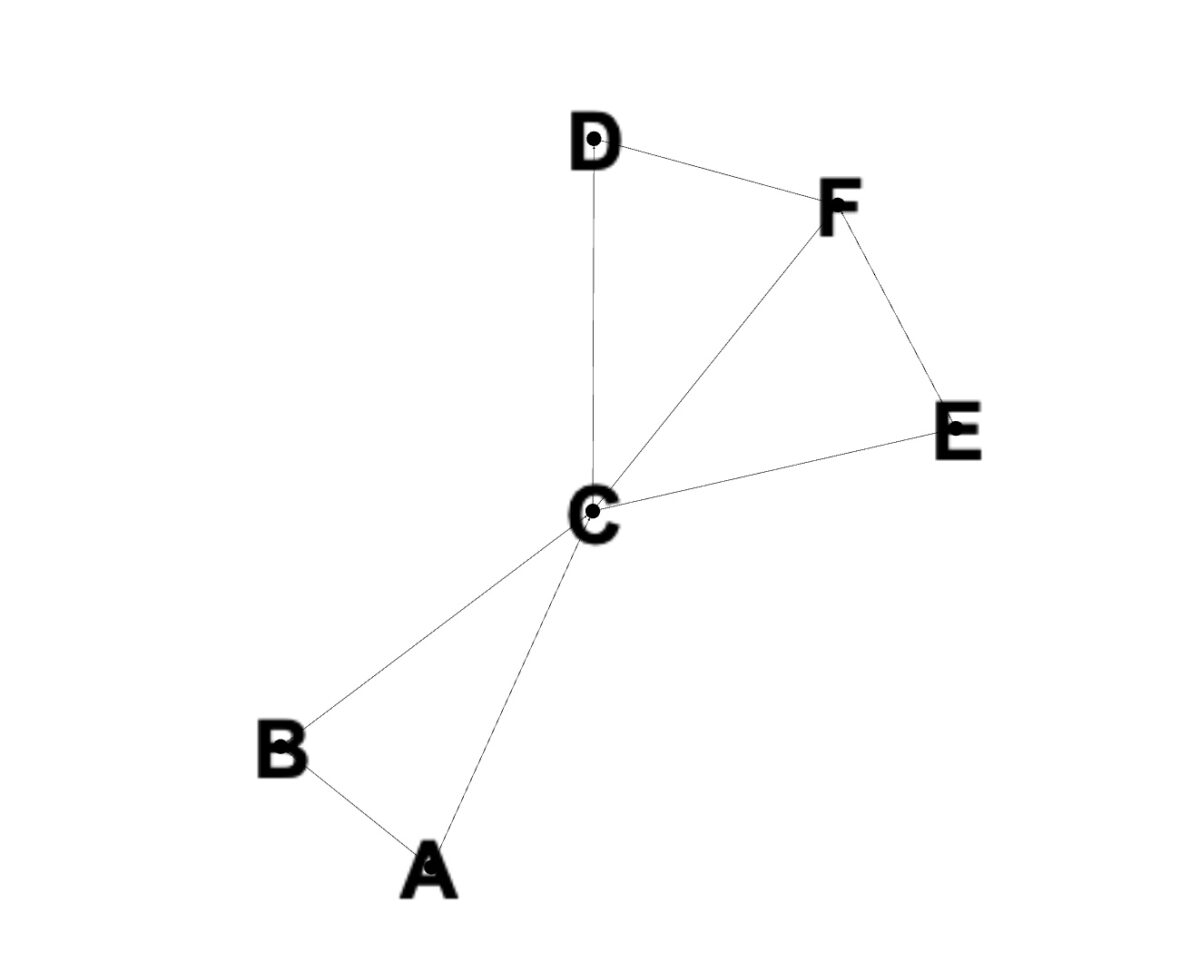 Wir werden dieses Diagramm für die folgenden Codebeispiele verwenden.
Wir werden dieses Diagramm für die folgenden Codebeispiele verwenden.
©”TNGD”.com
Nachdem die Grundlagen erklärt sind, ist es an der Zeit zu sehen, wie BFS in der Praxis funktioniert. Wir werden dies anhand eines Diagramms mit den Knoten A, B, C, D, E und F veranschaulichen, wie im Bild gezeigt. Der folgende Code zeigt, wie BFS für diesen Graphen mit der Programmiersprache Python implementiert wird.
from collections import defaultdict, deque def bfs(graph, start): queue=deque([start]) visited=set([start] ) while queue: node=queue.popleft() print(node) für Nachbar in graph[node]: falls Nachbar nicht in visited: visited.add(neighbor) queue.append(neighbor) graph=defaultdict(list) edges=[ (“A”,”B”),”A”,”C”), (“B”,”C”), (“C”,”D”), (“C”,”E”), (“C”,”F”), (“D”,”F”), (“E”,”F”) für Kante in Kanten: graph[edge[0]].append(edge[0]) graph[ edge[1]].append(edge[0]) bfs(graph,”A”)
Erklärung des Codes
Zunächst importieren wir die Klassen „defaultdict“ und „deque“. aus dem Modul „Sammlungen“. Diese werden verwendet, um ein Wörterbuch mit Standardschlüsselwerten und eine Warteschlange zu erstellen, die das Hinzufügen und Entfernen von Elementen ermöglicht.
Als Nächstes definieren wir die „bfs“-Funktion mit zwei Argumenten, „graph“ und”Start”. Wir nehmen das „Graph“-Argument als Wörterbuch mit den Scheitelpunkten als Schlüsseln und benachbarten Scheitelpunkten als Werten. Hier bezieht sich „start“ auf den Quellknoten, an dem der Algorithmus beginnt.
„queue=deque([start])“ erstellt eine Warteschlange mit dem Quellknoten als einzigem Element und „visited=set ([start])“ erstellt eine Menge besuchter Knoten mit dem Quellknoten als einzigem Element.
Die „while“-Schleife wird fortgesetzt, bis die Warteschlange leer ist. „node=queue.popleft()“ entfernt das Element ganz links aus der Warteschlange und speichert es in der Variable „node“. „print(node)“ gibt diese Knotenwerte aus.
Die „for“-Schleife iteriert über jeden Nachbarknoten. „Wenn Nachbar nicht besucht“ prüft, ob der Nachbar besucht wurde. „visited.add(neighbor)“ fügt den Nachbarn zur besuchten Liste hinzu, und „queue.append(neighbor)“ fügt den Nachbarn am rechten Ende der Warteschlange hinzu.
Danach erstellen wir einen Standardwert Wörterbuch namens „Graph“ und definieren die Kanten des Graphen. Die „for“-Schleife iteriert über jede Kante. „graph[edge[0]].append(edge[1])“ fügt das zweite Element der Kante als Nachbar des ersten Elements und das erste Element der Kante als Nachbar des zweiten hinzu. Dies konstruiert den Graphen.
Schließlich rufen wir die „bfs“-Funktion auf „graph“ auf, mit dem Quellknoten als „A“.
Implementierung des Codes
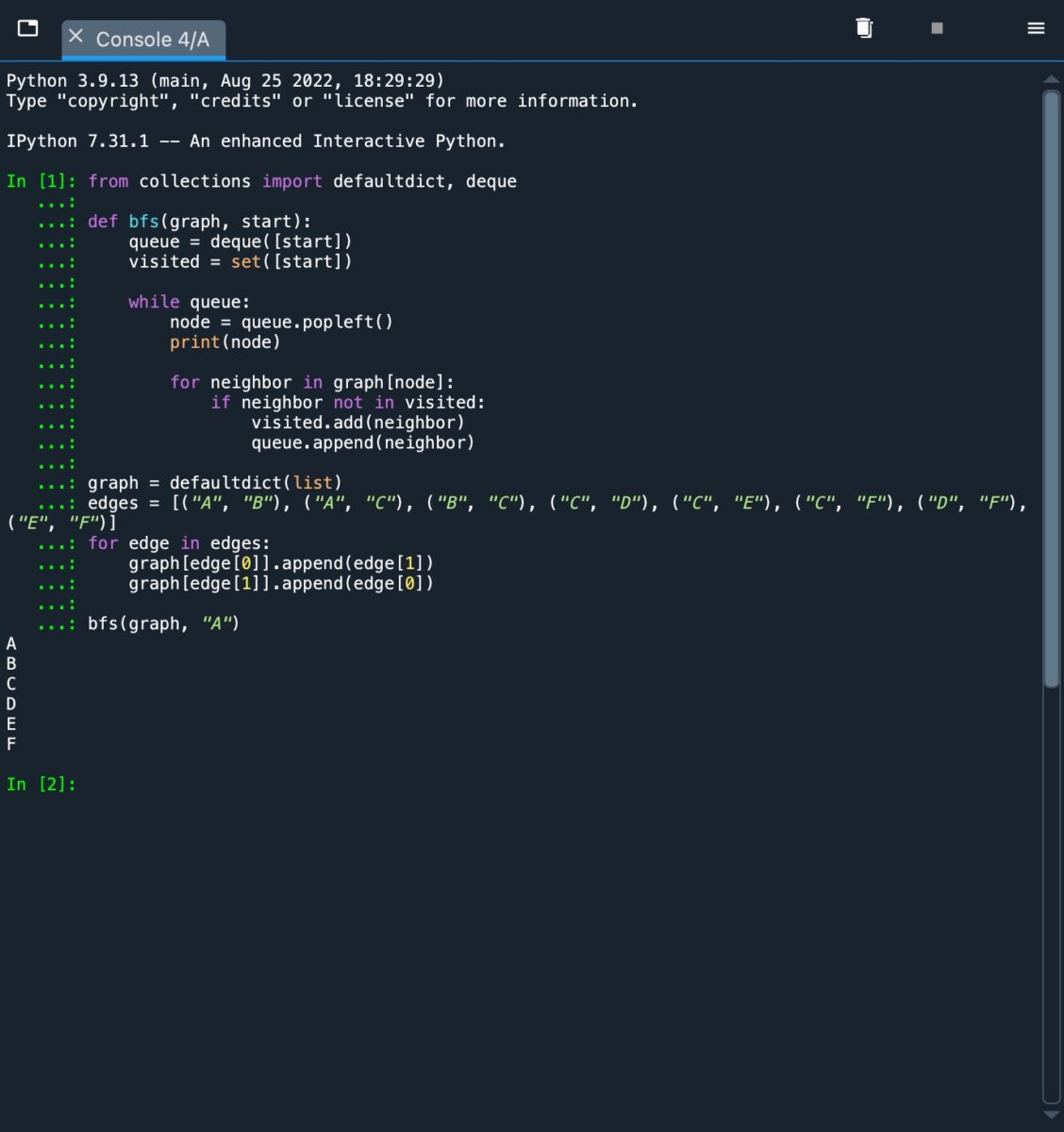 So sieht der BFS-Algorithmus wann aus implementiert und läuft durch einen verbundenen Graphen.
So sieht der BFS-Algorithmus wann aus implementiert und läuft durch einen verbundenen Graphen.
©”TNGD”.com
Im Screenshot sehen wir die Ausgabe [A, B, C, D, E F]. Das ist, was wir erwarten würden, da BFS die Knoten auf jeder Tiefenstufe erkundet, bevor es zur nächsten übergeht. Wenn wir uns wieder dem Diagramm zuwenden, sehen wir, dass B und C der Warteschlange hinzugefügt und zuerst besucht werden. B wird besucht, und dann werden A und C zur Warteschlange hinzugefügt. Da A bereits besucht wurde, wird C als nächstes besucht und A wird entfernt. Danach werden die Nachbarn von C, D, E und F, der Warteschlange hinzugefügt. Diese werden dann besucht und die Ausgabe gedruckt.
BFS für nicht verbundene Graphen verwenden
Wir haben zuvor BFS für einen verbundenen Graphen verwendet. Wir können BFS jedoch auch verwenden, wenn nicht alle Knoten verbunden sind. Wir werden dieselben Diagrammdaten verwenden, da der modifizierte Algorithmus mit beiden Arten von Diagrammen veranschaulicht werden kann. Der geänderte Code lautet:
from collections import defaultdict, deque def bfs(graph, start): queue=deque([start]) visited=set([start]) while queue: node=queue.popleft() print (Knoten) für Nachbar in graph[Knoten]: wenn Nachbar nicht besucht: visited.add(neighbor) queue.append(neighbor) für Knoten in graph.keys(): wenn Knoten nicht besucht: queue=deque([node ]) visited.add(node) while queue: node=queue.popleft() print(node) für Nachbar in graph[node]: falls Nachbar nicht in visited: visited.add(neighbor) queue.append(neighbor) graph=defaultdict(list) edges=[(“A”,”B”), (“A”,”C”), (“B”,”C”), (“C”,”D”), (“C”,”E”), (“C”,”F”), (“D”,”F”), (“E”,”F”)] für Kante in Kanten: graph[edge[0]]. append(edge[1]) graph[edge[1]].append(edge[0]) bfs(graph,”A”)
Wir haben eine zusätzliche „for“-Schleife verwendet. Die Schleife iteriert mit der Methode „graph.keys()“ über alle Knoten. BFS startet eine neue Warteschlange, wenn es einen nicht besuchten Knoten findet, und arbeitet rekursiv. Auf diese Weise besuchen wir alle getrennten Knoten. Eine Illustration finden Sie im Bild unten.
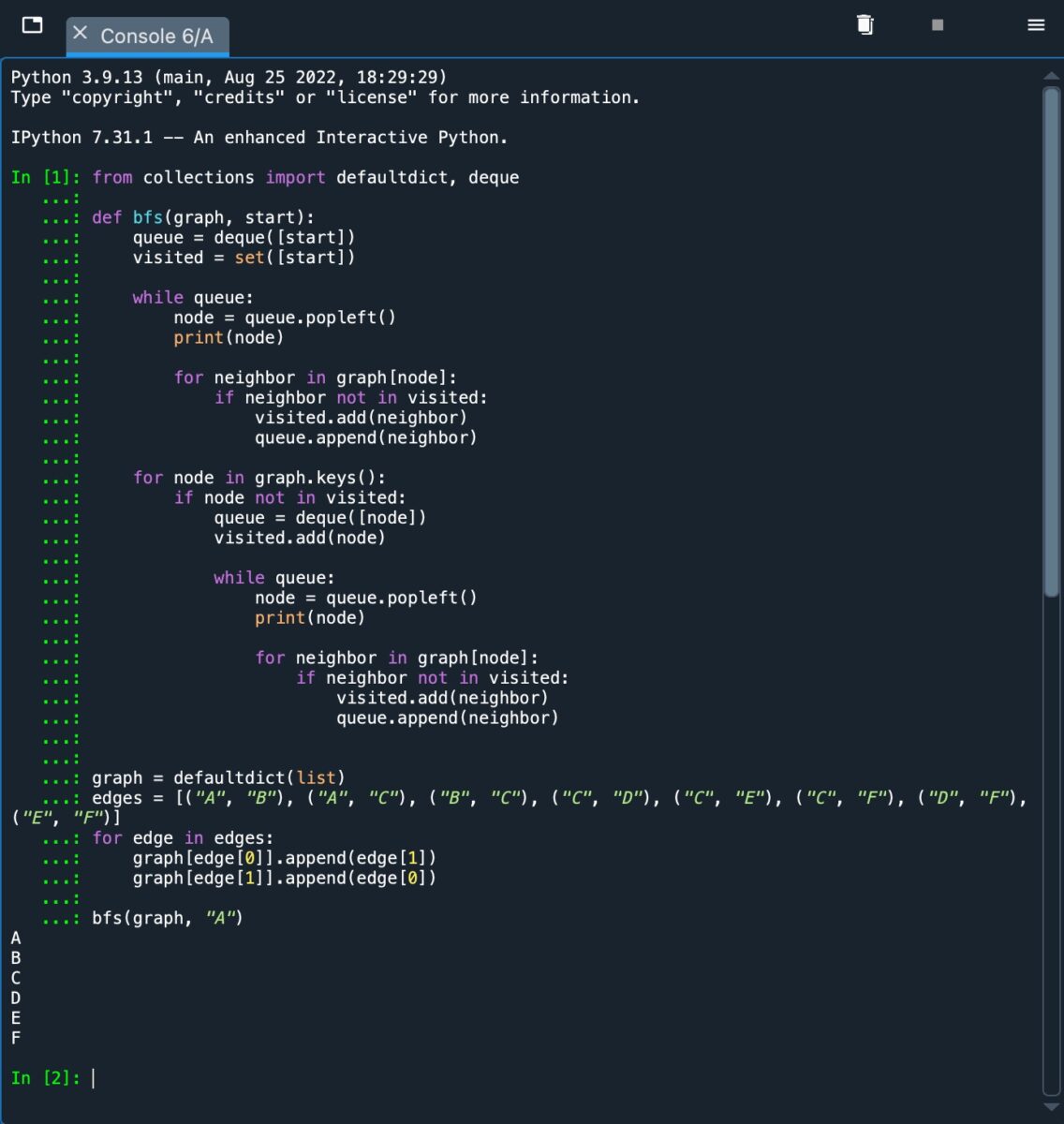 Dies ist ein Beispiel für den BFS-Algorithmus, wenn er implementiert ist und einen nicht verbundenen Graphen durchläuft.
Dies ist ein Beispiel für den BFS-Algorithmus, wenn er implementiert ist und einen nicht verbundenen Graphen durchläuft.
©”TNGD”.com
Beste und schlechteste Anwendungsfälle für BFS
Da wir jetzt wissen, wie BFS funktioniert, sollten wir uns die zeitliche und räumliche Komplexität des Algorithmus ansehen, um eine Vorstellung von seinen besten und schlechtesten Anwendungsfällen zu bekommen.
Zeitkomplexität von BFS
Wir können sehen, dass die Zeitkomplexität in allen Fällen gleich ist und gleich O(V + E), wobei V die Anzahl der Ecken und E die Anzahl der Kanten ist. Im besten Fall, wenn wir nur einen Knoten haben, ist die Komplexität O(1), weil V=1 und E=0. Im durchschnittlichen und im schlimmsten Fall besucht der Algorithmus alle Knoten, die er vom Quellknoten erreichen kann , also hängt die Komplexität in beiden Fällen von der Struktur und Größe des Graphen ab.
Raumkomplexität von BFS
Wieder sehen wir, dass die Komplexität für alle Fälle gleich ist. Der Algorithmus besucht jeden Knoten unabhängig von der Diagrammstruktur. Daher hängt die Komplexität von der Anzahl der Scheitelpunkte im Graphen ab.
Nachbereitung
BFS ist eine Möglichkeit, die Knoten in einem Graphen zu durchlaufen, Pfadentfernungen zu berechnen und Beziehungen zwischen ihnen zu untersuchen Knoten. Es ist ein sehr nützlicher Algorithmus zum Erkunden von Netzwerksystemen und zum Erkennen von Graphzyklen. BFS ist sowohl für verbundene als auch für nicht verbundene Graphen relativ einfach zu implementieren. Ein Vorteil ist, dass die zeitliche und räumliche Komplexität für alle Fälle gleich ist.
Breite-First-Suche (BFS) für Graphen – erklärt, mit Beispielen FAQs (häufig gestellte Fragen)
Was ist BFS?
BFS ist ein Algorithmus, der zum Durchlaufen von Bäumen oder Graphen verwendet wird, normalerweise solche, die Netzwerke wie soziale Netzwerke oder Computernetzwerke darstellen. Es kann auch Graphenzyklen erkennen oder ob ein Graph zweiteilig ist, sowie die kürzesten Pfadentfernungen berechnen. Breitengrad bedeutet, dass jeder Knoten in einer bestimmten Tiefe untersucht wird, bevor zum nächsten übergegangen wird.
Wie hoch ist die zeitliche Komplexität von BFS?
Die Die Zeitkomplexität von BFS ist in allen Fällen O(V + E).
Was ist die Raumkomplexität von BFS?
Die Raumkomplexität von BFS ist O(V) in allen Fällen.
Wann sollten Sie BFS verwenden?
Wenn Sie die kürzeste Pfadentfernung berechnen oder alle Scheitelpunkte darin erkunden müssen ein ungewichtetes Diagramm.
Wie wird BFS implementiert?
Wir implementieren BFS typischerweise mit einer Warteschlangendatenstruktur und einem Satz, um besuchte und nicht besuchte Knoten zu verfolgen. Der Quellknoten wird der Warteschlange hinzugefügt und als besucht markiert. Dann bearbeitet der Algorithmus rekursiv benachbarte Knoten und fügt Knoten hinzu und entfernt sie, um sicherzustellen, dass kein Knoten zweimal besucht wird.
Wie schneidet BFS im Vergleich zu Dijkstras Algorithmus ab?
Diese Algorithmen können beide verwendet werden, um kürzeste Pfadentfernungen zu berechnen, aber BFS arbeitet mit ungewichteten Graphen. Im Gegensatz dazu arbeitet der Dijkstra-Algorithmus mit gewichteten Graphen.
Wie unterscheidet sich DFS von BFS?
Beide werden verwendet, um einen Graphen zu durchlaufen, aber sie unterscheiden sich darin wie sie das machen. Während BFS jeden Knoten in einer bestimmten Tiefe durchsucht, bevor es weitergeht, besucht DFS Knoten in einer möglichst tiefen Tiefe, bevor es zu sich selbst zurückkehrt, um einen anderen Zweig zu erkunden. DFS verwendet normalerweise eine Stack-Datenstruktur im Gegensatz zu einer Warteschlange.