© BEST-BACKGROUNDS/Shutterstock.com
Wenn es darum geht, eine Reihe von Daten zu sortieren, gibt es viele Sortieralgorithmen, die Sie verwenden können. Einer der am einfachsten zu verwendenden Algorithmen ist Insertion Sort, aufgrund seiner relativen Einfachheit und intuitiven Natur. Lesen Sie weiter, um anhand eines Beispiels genau zu erfahren, was Insertion Sort ist, wie es implementiert ist und wofür es verwendet werden kann.
Was ist Insertion Sort?
Insertion Sort ist eine Sortierung Algorithmus, eine der Methoden, die Sie verwenden können, um ein Array zu sortieren. Die Funktionsweise ist nicht zu kompliziert zu verstehen und kann weitgehend damit verglichen werden, wie Sie ein Kartenspiel sortieren würden.

In In diesem Fall würden wir zunächst davon ausgehen, dass die erste Karte im Deck bereits sortiert ist. Dann wählen wir eine unsortierte Karte aus und sortieren sie. Dies geschieht durch einen Vergleich mit der ersten Karte. Wenn die ausgewählte Karte größer ist als die sortierte Karte, wird sie in eine Position rechts von der ersten Karte gelegt. Wenn die betreffende Karte kleiner ist als die sortierte Karte, wird sie in eine Position links platziert.
Dieser Vorgang wird fortgesetzt, bis alle unsortierten Karten an ihren richtigen Positionen platziert sind. Insertion Sort funktioniert auf sehr ähnliche Weise. Jeder unsortierte Datenwert wird durch denselben iterativen Prozess sortiert.
Da Insertion Sort ein recht einfacher Algorithmus ist, wird er am besten für relativ kleine Datensätze sowie für solche verwendet, die bereits einigermaßen sortiert sind. Auf diese Weise ist es als adaptiver und effizienter Algorithmus bekannt. Als nächstes gehen wir die Theorie hinter der Funktionsweise von Insertion Sort durch.
Der Algorithmus hinter Insertion Sort
Die Insertion Sort-Methode kann mit dem folgenden Pseudocode prägnant dargestellt werden:
insertSort(array) markiere erstes Element als sortiert für jedes unsortierte Element X’extrahiere’das Element X für j-lastSortedIndex auf 0, wenn aktuelles Element j > X sortiertes Element um 1 nach rechts verschiebt Schleife unterbrechen und hier X einfügen end insertSort
Einfach ausgedrückt bedeutet dies, dass das erste Element als sortiert angenommen wird. Jedes nachfolgende Element wird mit dem ersten Element verglichen. Wenn es kleiner als das sortierte Element ist, wird es an die erste oder nullte Position verschoben. Wenn es größer ist, wird es um eine Position nach rechts verschoben. Iterationen werden fortgesetzt, bis alle Elemente sortiert wurden.
Das Innenleben von Insertion Sort
Jetzt haben wir die Funktionsweise von Insertion Sort und die Theorie dahinter behandelt. Es ist Zeit, den Prozess zu veranschaulichen mit einem passenden Array. Betrachten wir den folgenden Datensatz:
Wir können davon ausgehen, dass das erste Element, 10, bereits sortiert ist. Danach nehmen wir das zweite Element, 14, und speichern es separat. Wenn wir 14 mit 10 vergleichen, können wir sehen, dass es größer ist, also behält es seine Position als zweites Element. Dies ist die erste Iteration, die als erster Durchlauf bezeichnet wird. Das erste Element, 10, wird in einem Subarray gespeichert.
Wo grün=sortiertes Array
Für den zweiten Durchgang gehen wir weiter zum dritten Element, das 5 ist. Dies ist im Vergleich zu den vorherigen Elementen. Wir können erkennen, dass es kleiner ist als das vorherige Element, 14, also tauscht es die Plätze mit 14.
Der Algorithmus vergleicht es dann mit den Elementen im sortierten Subarray. 5 ist auch kleiner als 10, also wird es an den Anfang des Subarrays verschoben. Das sortierte Array hat jetzt 2 Elemente – 5 und 10.
Jetzt gehen wir zum dritten Durchgang über. In diesem Fall ist 7 das ausgewählte Element. Dies ist kleiner als 14, also wird es um eine Position nach links und in das sortierte Array verschoben. Dies ist jedoch nicht die richtige Position, da 7 kleiner als 10, aber größer als 5 ist. Daher wird es um eine weitere Position nach links verschoben.
Für den vierten Durchgang betrachten wir den vierten Element, das 14 ist. Dies ist bereits sortiert, also enthält das sortierte Array jetzt 5, 7, 10 und 14.
Das Endergebnis
Schließlich, für den fünften Durchgang, wir nehmen das fünfte Element, das ist 1. Das ist deutlich kleiner als 14, also wird die Position getauscht. Es ist auch kleiner als 10, also wird die Position wieder getauscht. Dies wird noch zweimal fortgesetzt, da 1 das kleinste Element im Array ist. Daher erhalten wir am Ende ein sortiertes Array wie folgt:
Die Implementierung von Insertion Sort
Insertion Sort kann mit einer Vielzahl von Programmiersprachen implementiert werden, von C, C# und C++ zu Java, Python, PHP und Javascript. Zur Veranschaulichung werden wir mit Python arbeiten. Der gesamte Vorgang kann in folgendem Code dargestellt werden:
def insertSort(arr): if (n:=len(arr))=1: return for i in range(1, n): key=arr[i ] j=i-1 while j >=0 and key arr[j]: arr[j+1]=arr[j] j-=1 arr[j+1]=key arr=[10, 14, 5, 7, 1] insertSort(arr) print(arr)
Zunächst definieren wir die Einfügesortierung als Funktion des Arrays (arr). Dann sagen wir, dass, wenn das Array die Länge 1 oder weniger hat, das Array zurückgegeben wird. Als nächstes definieren wir das Element an der i-ten Position eines Arrays der Länge n als Schlüssel.
Wir schränken die Berechnung so ein, dass j nur bearbeitet wird, wenn es größer oder gleich Index 0 ist. J wird als der Wert links von dem betrachteten Element betrachtet, as pro j=i-1. Wenn sein Wert größer als der Schlüssel ist, wird seine Position nach rechts verschoben.
Die letzte Zeile, arr[j+1]=key, diktiert, dass der Wert rechts von diesem j-Wert der neue Schlüssel wird. Daher werden die restlichen Nummern nach Bedarf vertauscht. Dieser Prozess wird dann von Anfang an fortgesetzt, bis alle Zahlen korrekt sortiert sind.
Insertion Sort in Python: Implementierung
Sehen wir uns an, wie dies in Python innerhalb der Spyder-Umgebung implementiert wird. Wir verwenden dasselbe Array wie zuvor, um dies klar zu veranschaulichen. Siehe den implementierten Code unten:
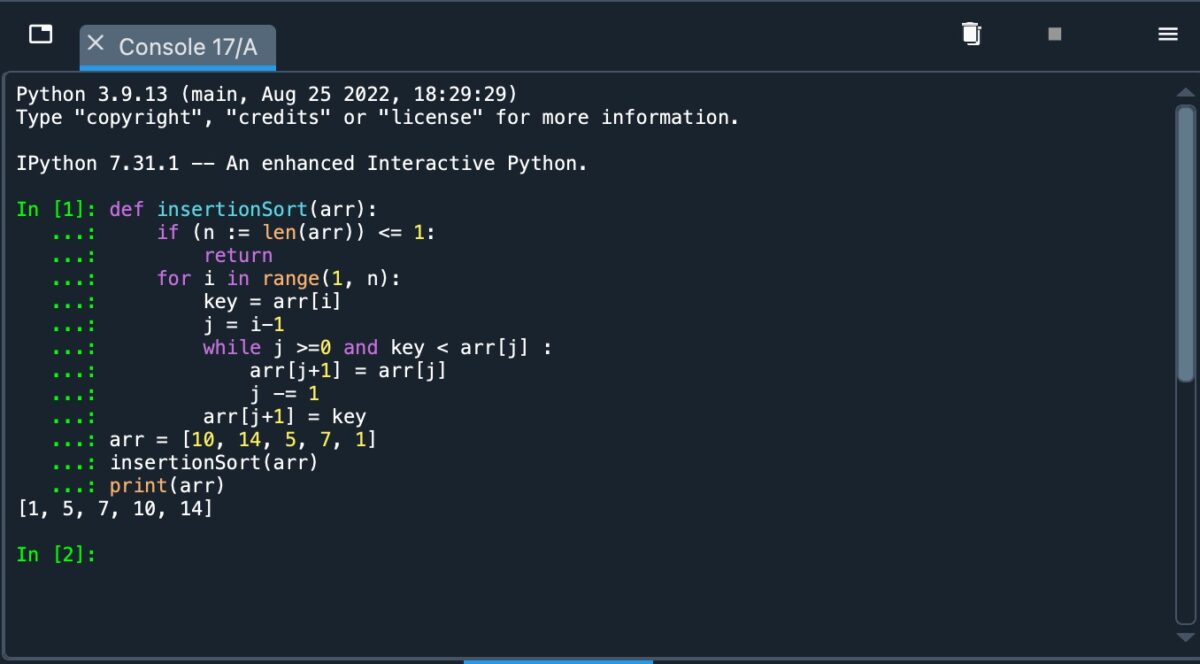 Implementing Insertion Sort in Python.
Implementing Insertion Sort in Python.
©”TNGD”.com
Eine wichtige Erkenntnis ist, dass die Einrückung bei der Verwendung von Python entscheidend ist. Wenn die Einrückung nicht richtig verwendet wird, erhalten Sie eine Fehlermeldung, die wie unten aussieht.
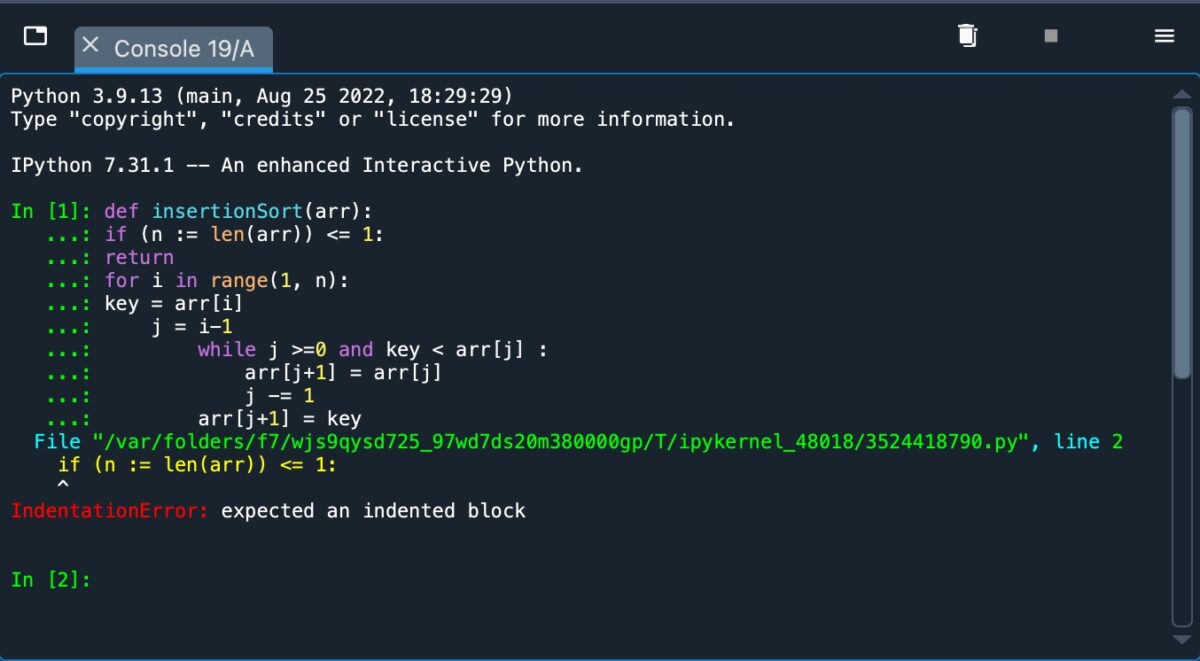 Erhalte eine Fehlermeldung.
Erhalte eine Fehlermeldung.
©”TNGD”.com
Beste und schlechteste Anwendungsfälle von Insertion Sort
Während Insertion Sort für viele Zwecke nützlich ist, wie bei jedem Algorithmus, hat es seine besten und schlechtesten Fälle. Dies liegt hauptsächlich an der Zeit-und Platzkomplexität.
Zeitkomplexität mit Insertion Sort
Die Zeitkomplexität kann in jedem Fall in der folgenden Tabelle beschrieben werden:
Sie sehen, dass die Zeitkomplexität im besten Fall gleich O(n) ist. Das bedeutet, dass keine Sortierung erforderlich ist, da das Array bereits sortiert ist. Da der Algorithmus jeden Wert nacheinander überprüfen muss, bevor er feststellen kann, dass das Array sortiert ist, ist die Zeitkomplexität linear. Das heißt, die Komplexität ist linear proportional zur Größe der Eingabe.
Im Durchschnitt und im schlimmsten Fall ist die Komplexität jedoch gleich O(n2). Ein durchschnittlicher Fall wäre, wenn die Elemente im Array durcheinander geraten, weder aufsteigend noch absteigend. Im schlimmsten Fall müssten die Elemente umgekehrt sortiert werden.
Das liegt daran, dass sie bereits in aufsteigender oder absteigender Reihenfolge sind und Sie die umgekehrte Reihenfolge benötigen. Diese Art von Komplexität wird als quadratische Zeit bezeichnet, da sie von n2 abhängt. Wenn beispielsweise die Größe der Eingabe 4 ist, wäre die Anzahl der Operationen 16.
Leerzeichenkomplexität mit Insertion Sort
Die andere Art von Komplexität ist Leerzeichenkomplexität. Dies bezieht sich auf die Menge an Speicherplatz, die zum Ausführen des Algorithmus benötigt wird. Eine Komplexität von O(1) bedeutet, dass die benötigte Speichermenge unabhängig von der Eingabegröße konstant ist.
Dies gilt im Fall von Insertion Sort, da Sie bei jeder Operation nur eine temporäre Variable verwenden. Mit anderen Worten, es wird immer nur ein Wert sortiert, sodass die Speichernutzung konstant ist.
Es sollte beachtet werden, dass Insertion Sort als stabiler Algorithmus betrachtet wird, was bedeutet, dass die relative Reihenfolge von Elementen mit gleichen Werten stabil ist konserviert. Dies ist hilfreich, wenn Sie die Reihenfolge bestimmter Elemente beibehalten oder Arrays sortieren müssen, die bereits teilweise sortiert sind. Dies liegt daran, dass Elemente nicht mit dem Schlüssel ausgetauscht werden, wenn sie diesem entsprechen.
Zusammenfassung
Wir haben behandelt, was Insertion Sort ist und wann es sinnvoll ist, es zu verwenden. Darüber hinaus haben wir seine zeitliche und räumliche Komplexität berücksichtigt und seine Codedarstellung und-implementierung in Python gezeigt. Wenn Sie ein relativ kleines Array sortieren möchten, insbesondere eines, in dem einige Elemente bereits sortiert sind, ist Insertion Sort eine der besten Methoden.
Als Nächstes
Was ist Insertion Sort und wie funktioniert es? (Mit Beispielen) FAQs (Frequently Asked Questions)
Was ist Insertion Sort?
Insertion Sort ist ein Algorithmus, der zum Sortieren von Datensätzen verwendet werden kann aufsteigende oder absteigende Reihenfolge. Es ist ähnlich, wie Sie ein Kartenspiel in Ihren Händen sortieren würden, da das erste Element als sortiert betrachtet wird.
Jedes nachfolgende Element wird dann mit dem ersten Element verglichen und an der richtigen Position platziert, wobei es entweder dort bleibt, wo es ist, oder um eine Position nach rechts verschoben wird. Dies wird für jedes Element wiederholt, und dann wird der Vorgang von Anfang an fortgesetzt, bis alle Elemente sortiert sind.
Wann sollten Sie Insertion Sort verwenden?
Insertion Sort wird am besten für kleine Datensätze und solche verwendet, bei denen die Werte bereits teilweise sortiert sind.
Welche Programmiersprachen können Insertion Sort implementieren?
Viele aller Programmiersprachen können Insertion Sort implementieren, einschließlich C, C++, C#, Java, Javascript, PHP und Python.
Welche Vorteile hat Insertion Sort?
Die Vorteile von Insertion Sort sind, dass es einfach ist, die relative Reihenfolge der Schlüssel sich nicht ändert, dass es effizient für kleine Datensätze ist und dass es eine Liste sortieren kann, während sie empfangen wird.
Wie wird die Einfügungssortierung optimiert?
Die Einfügungssortierung wird optimiert, indem ein gespeichertes Subarray erstellt wird, in dem sortierte Werte vorübergehend gespeichert werden. Dies bedeutet, dass ein vollständiger Austausch der Array-Elemente während jeder Iteration nicht erforderlich ist, da die Elemente einzeln ausgetauscht werden.
Wie viele Iterationen gibt es bei Insertion Sort?
Bei einem Array der Länge n sind n-1 Iterationen erforderlich, um das gesamte Array zu sortieren.
Wie kann die Einfügungssortierung geändert werden?
Einfügungssortierung kann durch binäre Einfügungssortierung geändert werden. Dies ähnelt Insertion Sort darin, dass es ein stabiler Algorithmus ist, aber es reduziert die Anzahl der Vergleiche, die durchgeführt werden müssen.
Die Zeitkomplexität wird von O(n) auf O(log n) reduziert, weil Es verwendet eine binäre Suche anstelle einer linearen Suche. Jeder Wert wird mit den Werten in dem sortierten Subarray verglichen, um zu bestimmen, welcher Wert gerade größer als der ausgewählte Wert ist. Dies verkürzt die Anzahl der Operationen.
Welche Nachteile hat Insertion Sort?
Insertion Sort ist nicht für besonders große Datensätze geeignet, da die Die Zeitkomplexität ist im Durchschnitt und im schlimmsten Fall quadratisch.
Welche Alternativen gibt es zur Einfügungssortierung?
Bei großen und durcheinandergebrachten Datensätzen geeignetere Alternativen sind Quick Sort, Merge Sort oder Heap Sort.
Ist Insertion Sort ein stabiler Algorithmus?
Ja, Insertion Sort wird als stabiler Sortieralgorithmus betrachtet, weil Elemente unverändert bleiben, wenn sie gleich dem Schlüssel sind. Die Reihenfolge der Elemente wird auch beibehalten, wenn sie einander äquivalent sind.