Es gibt tatsächlich zwei Möglichkeiten, Mergesort zu implementieren – den Top-down-Ansatz und den Bottom-up-Ansatz. Es ist ein guter Zeitpunkt, um einen kurzen Überblick über diese Prozesse zu geben.
Der Top-Down-Ansatz
Wie der Name schon sagt, beginnt dieser Algorithmus ganz oben mit dem anfänglichen Array, teilt das Array in zwei Hälften, sortiert diese Unterarrays rekursiv (d. h. durch Aufteilen und Wiederholen des Vorgangs) und fügt dann die Ergebnisse zu einem sortierten Array zusammen.
Der Bottom-up-Ansatz
Der Bottom-up-Ansatz hingegen beruht auf einer iterativen Methode. Es beginnt mit einem Array aus einem einzelnen Element und führt dann die Elemente auf beiden Seiten zusammen, während sie sortiert werden. Diese kombinierten und sortierten Arrays werden zusammengeführt und sortiert, bis nur noch ein Element im sortierten Array verbleibt. Der Hauptunterschied besteht darin, dass, während der Top-Down-Ansatz jedes Subarray rekursiv sortiert, der Bottom-Up-Ansatz das Array in einzelne Arrays zerlegt. Dann wird jedes Array iterativ sortiert und zusammengeführt.
Funktionsweise von Merge Sort
Im Anschluss daran wäre ein funktionierendes Beispiel für die Verwendung von Merge Sort nützlich.
Sagen wir wir habe ein Array, arr. Arr=[37, 25, 42, 2, 7, 89, 14].
Zunächst prüfen wir, ob der linke Index des Arrays kleiner als der rechte Index ist. Wenn dies zutrifft, wird der Mittelpunkt berechnet. Dies ist gleich „(start_index“ + („end_index“-1))/2, was in diesem Fall 3 ist. Daher ist das Element bei Index 3 der Mittelpunkt, der 2 ist.
Auf diese Weise wurde dieses Array aus 7 Elementen in zwei Arrays der Größe 4 und 3 für das linke bzw. rechte Teilarray aufgeteilt:
Linkes Array=[37, 25, 42, 2]
Rechtes Array=[7, 89, 14]
Wir fahren fort, indem wir den Mittelpunkt erneut berechnen und die Arrays in zwei teilen, bis eine Teilung nicht mehr möglich ist. Das Endergebnis ist:
[37], [25], [42], [2], [7], [89], [14]
Und dann wir kann mit dem Zusammenführen und Sortieren dieser Subarrays wie folgt beginnen:
[25, 37], [2, 42], [7,89], [14]
Diese Subarrays werden dann zusammengeführt und erneut sortiert, um Folgendes zu erhalten:
[2, 25, 37, 45] und [7, 14, 89]
Schließlich werden diese Subarrays zusammengeführt und sortiert, um das endgültige Sortierergebnis zu erhalten array:
[2, 7, 14, 25, 37, 45, 89]
Implementierung von Merge Sort
Mittlerweile haben wir behandelt wie der Merge-Sort-Algorithmus funktioniert, die beteiligten Schritte und die Arbeit dahinter anhand eines Beispiels. Es ist also endlich an der Zeit zu sehen, wie dieser Algorithmus mithilfe von Code implementiert wird. Zur Veranschaulichung verwenden wir die Programmiersprache Python. Der Vorgang kann mit folgendem Code beschrieben werden:
def mergeSort(arr): if len(arr) > 1: mid=len(arr)//2 L=arr[:mid] R=arr[mid: ] mergeSort(L) mergeSort(R) i=j=k=0 while i len(L) and j len(R): if L[i]=R[j]: arr[k]=L[i] i +=1 sonst: arr[k]=R[i] j +=1 k +=1 while i len(L): arr[k]=L[i] i +=1 k +=1 while j len( R): arr[k]=R[j] j +=1 k +=1 def printList(arr): for i in range(len(arr)): print(arr[i], end=””) print () if__name__==’__main__’: arr=12, 11, 13, 5, 6, 7] print(“Gegebenes Array ist”, end=”\n”) printList(arr) mergeSort(arr) print(“Sorted array is”, end=”\n”) printList(arr)
Das sieht nach viel Code aus, aber es ist überschaubar, wenn wir es aufschlüsseln.
Erklärung der code
Zunächst definieren wir die Funktion mergeSort als Funktion des Arrays „arr“.
Die erste „if“-Anweisung prüft, ob die Länge des Arrays größer als ist 1. Wenn dies der Fall ist, können wir mit dem Teilen des Arrays fortfahren.
Dann berechnen wir den Mittelpunkt des Arrays und teilen es in zwei Unterarrays auf, „L“ und „R“.
Die Funktion mergeSort wird rekursiv auf L und R aufgerufen und teilt sie, bis jedes Subarray nur noch ein Element enthält.
An diesem Punkt werden drei Variablen auf Null=i, j und k initialisiert. Die ersten beiden sind die Anfangs-und Endindizes des Subarrays, an dem gearbeitet wird. „k“ ist eine Variable, die die aktuelle Position im Array verfolgt.
Der nächste Teil, beginnend mit der „while“-Anweisung, ist der Hauptabschnitt des Algorithmus. Der Algorithmus wird über L und R iteriert, vergleicht die Elemente bei i und j und kopiert das kleinere Element in das Array. Zusammen mit k werden diese Indexvariablen gemäß dem Inkrementoperator „=-“ inkrementiert.
Der nächste Abschnitt der „while“-Anweisungen schreibt vor, dass alle verbleibenden Elemente in den beiden Arrays in das ursprüngliche Array kopiert werden.
Wir sind fast fertig. Als nächstes definieren wir die Drucklistenfunktion als Funktion des Arrays „arr“.
Zu guter Letzt verwenden wir die Zeile „if_name_==’_main_’“, um sicherzustellen, dass der Code nur ausgeführt wird, wenn das Skript ausgeführt wird direkt ausgeführt werden und nicht, wenn es importiert wird.
Das ursprüngliche Array wird als „Gegebenes Array ist“ gedruckt, und das endgültige, sortierte Array wird als „Sortiertes Array ist“ gedruckt. Die letzte Zeile gibt dieses sortierte Array aus, nachdem das anfängliche Array gemäß dem vorherigen Code zusammengeführt und sortiert wurde.
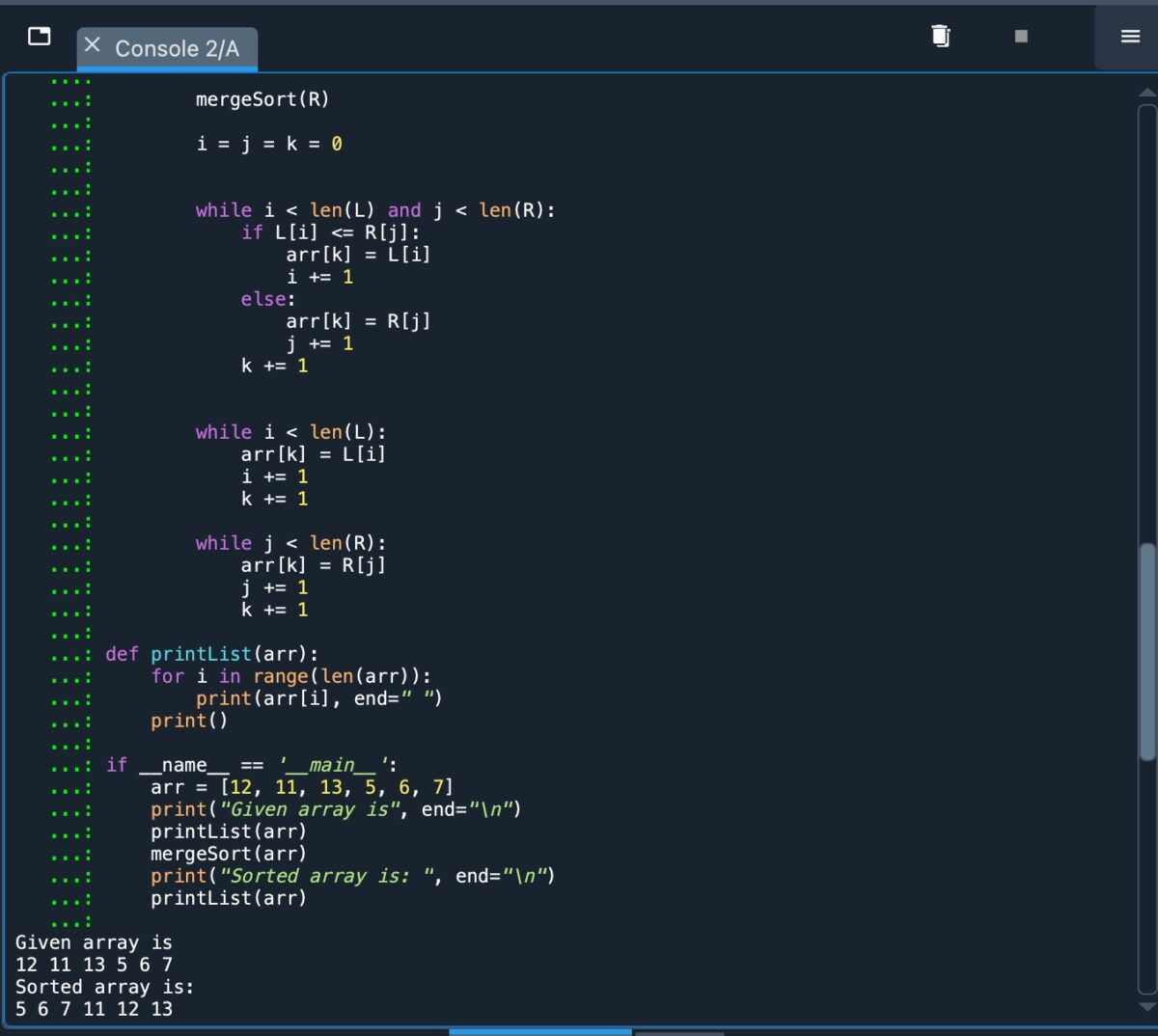
Zum Schluss noch ein Screenshot, der diesen Code zeigt, wie er in Python implementiert wird:
Python-Code für den Merge-Sort-Algorithmus.
©”TNGD”.com
Beste und schlechteste Anwendungsfälle von Insertion Sort
Merge-Sort ist ein einfacher Algorithmus, aber wie jeder Algorithmus , hat seine besten Anwendungsfälle und schlimmsten Fälle. Diese werden unten in Bezug auf Zeitkomplexität und Raumkomplexität dargestellt.
Zeitkomplexität mit Insertion Sort
Die Zeitkomplexität kann in jedem Fall in der folgenden Tabelle beschrieben werden:
Der beste Fall bezieht sich darauf, wenn das Array teilweise sortiert ist, der durchschnittliche Fall bezieht sich darauf, wenn das Array durcheinander ist und der schlimmste Fall bezieht sich darauf, wenn das Array in aufsteigender oder absteigender Reihenfolge ist und Sie das Gegenteil wollen. Als solches würde dies die meiste Sortierung erfordern.
Glücklicherweise hat die Zusammenführungssortierung in jedem Fall die gleiche Zeitkomplexität von O(n log n). Denn jedes Element muss in jedem Fall kopiert und verglichen werden. Dies führt zu einer logarithmischen Abhängigkeit von der Eingabegröße, da das Array rekursiv geteilt wird, bis jedes Subarray ein Element enthält. In Bezug auf Sortieralgorithmen ist die Zeitkomplexität von Mergesort besser als bei einigen anderen, wie z. B. Insertion Sort und Selection Sort. Daher ist Merge Sort einer der besten Sortieralgorithmen für die Arbeit mit großen Datensätzen.
Als Nächstes untersuchen wir die Raumkomplexität von Merge Sort.
Raumkomplexität von Merge Sort
Im Vergleich zu anderen Sortieralgorithmen schneidet die Platzkomplexität von Merge Sort nicht ganz so gut ab. Anstelle einer Komplexität von O (1) (wobei die Speichernutzung konstant ist und nur eine temporäre Variable gespeichert wird) hat Mergesort eine Speicherplatzkomplexität von O (n), wobei n die Eingabegröße ist. Im schlimmsten Fall müssen n/2 temporäre Arrays erstellt werden, die jeweils eine Größe von n/2 haben. Dies bedeutet einen Platzbedarf von O(n2/4) oder O(n2). Aber im Durchschnitt und im besten Fall ist die Anzahl der benötigten Arrays log(n) zur Basis 2, was bedeutet, dass die Komplexität proportional zu n ist. Insgesamt ist die Komplexität von Merge Sort relativ gut und der Algorithmus eignet sich für große Datensätze, aber der Speicherverbrauch ist signifikanter als bei anderen Methoden.
Zusammenfassung
Abschließend, Die Vor-und Nachteile des Merge-Sort-Algorithmus wurden erklärt, zusammen mit der Funktionsweise des Algorithmus, illustriert mit Beispielen. Merge Sort ist ein geeigneter Sortieralgorithmus für große Datensätze, auch wenn der Speicherverbrauch relativ hoch ist. Kurz gesagt, es ist ein relativ einfach zu verstehender Algorithmus, der sich hervorragend in vielen Umgebungen implementieren lässt.