Was ist Quick Sort und wie funktioniert es? (Mit Beispielen)

© whiteMocca/Shutterstock.com

Sortieralgorithmen lassen sich normalerweise in zwei Lager einteilen – einfach zu implementieren oder schneller auszuführen. Die schnelle Sortierung fällt meistens in die letztere Kategorie. Lesen Sie weiter, um herauszufinden, wie Sie diesen Algorithmus implementieren und in welchen Situationen Sie ihn am besten verwenden können.

Was ist Quick Sort?

Quick Sort ist ein Sortieralgorithmus, der zum Organisieren von Arrays von verwendet wird Daten. Es beruht im Wesentlichen auf dem Prinzip „Teile und herrsche“. Dies ist die Methode, mit der wir ein größeres, komplexeres Problem in einfachere Teilprobleme aufteilen. Diese Teilprobleme werden dann gelöst und die Lösungen kombiniert, um die Lösung für das ursprüngliche Problem zu finden.

Der Algorithmus hinter Quick Sort

Dies ist nicht genau, wie man Quick Sort implementiert, gibt aber eine Vorstellung davon, wie es funktioniert funktioniert.

//i-> Startindex, j–> Endindex Quicksort(array, i, j) { if (i j) { pIndex=Partition(A, i, j) Quicksor(A,i, pIndex-1) Quicksort(A,pIndex+1, end) } }

Zunächst definieren wir Quicksort als Funktion eines Arrays mit einem Startelement und einem Endelement. Die „if“-Anweisung prüft, ob das Array mehr als ein Element enthält.

In diesem Fall rufen wir die „partition“-Funktion auf, die uns den Index des „Pivot“-Elements liefert. Dies trennt das Array in zwei Subarrays mit Elementen, die kleiner bzw. größer als der Pivot sind.

Die Funktion wird rekursiv für jedes Subarray aufgerufen, bis jedes Subarray nur noch ein Element hat. Das sortierte Array wird dann zurückgegeben und der Vorgang ist abgeschlossen.

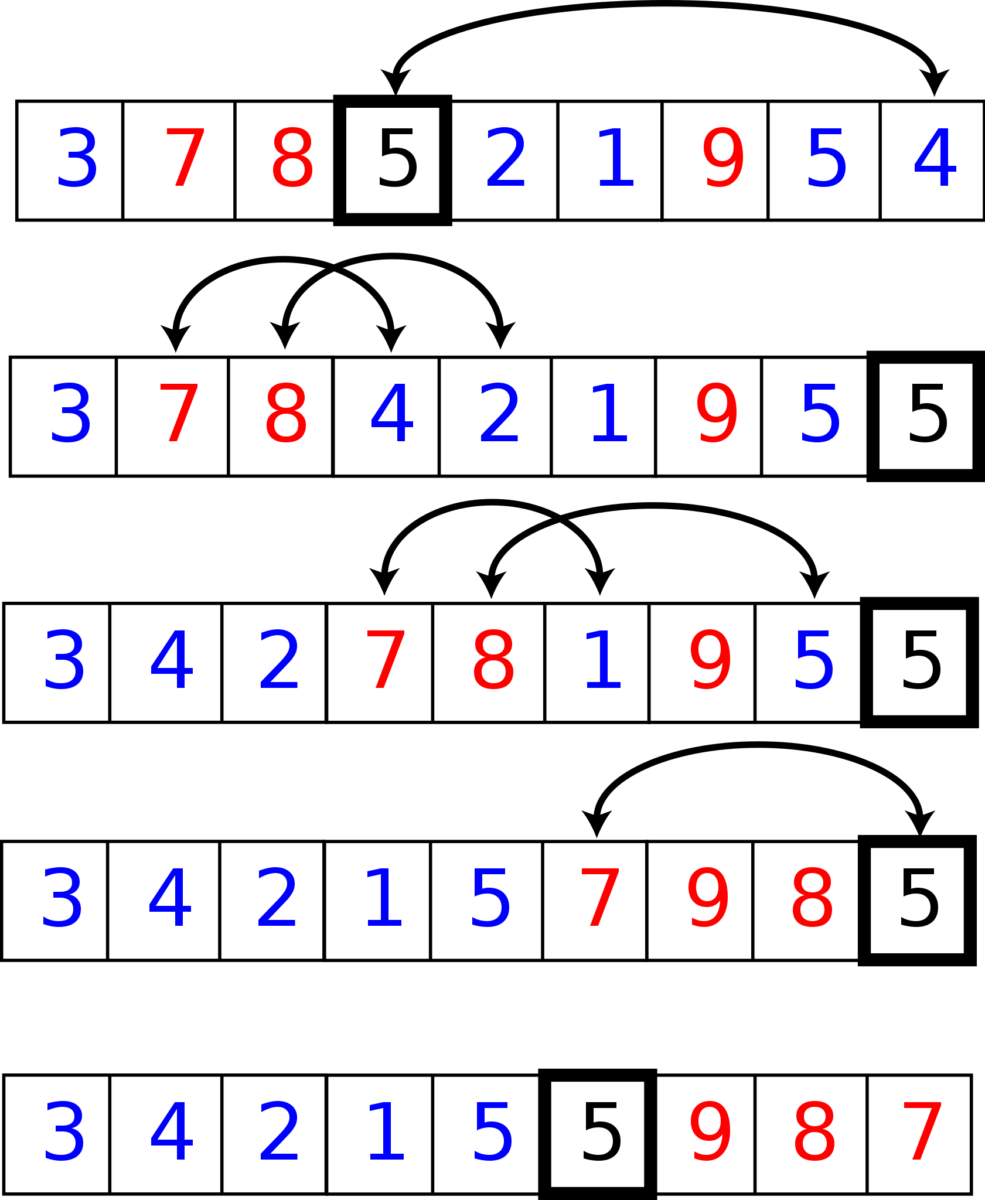In diesem Beispiel ist das eingerahmte Element das Pivot-Element, blaue Elemente sind gleich oder kleiner und rote Elemente sind größer.

©Dcoetzee/Public Domain – Lizenz

Ein Beispiel für schnelles Sortieren

Wie bei den meisten Dingen schnell sort lässt sich am besten anhand eines Beispiels erklären.

Nehmen wir das folgende Array – [56, 47, 98, 3, 6, 7, 11]

Wir haben Indizes von 0 bis 6 (denken Sie daran, dass das erste Element Index 0 ist, nicht 1).

Wenn Sie das letzte Element als Drehpunkt nehmen, wird das Array neu angeordnet, sodass Elemente, die kleiner als der Drehpunkt sind, auf der linken Seite stehen, und größere Elemente sind auf der rechten Seite. Dies geschieht durch Initialisieren der i-und j-Variablen auf 0. Wenn arr[j] oder das aktuelle Element kleiner als der Pivot ist, tauschen wir es mit arr[i] aus und tun dies inkrementell. Der Pivot wird dann mit arr[i] vertauscht, sodass dieses Element an seiner sortierten Position steht.

Das ergibt die Subarrays [6, 7, 3] und [56, 47, 98]. Der Index des Pivot-Elements ist jetzt 3 statt 6.

Dann wird Quicksort aufgerufen, das das linke Subarray um das Pivot-Element 3 herum sortiert, indem die Subarrays [6] und [7] sortiert werden.

Wir rufen dann Quick Sort rekursiv für das rechte Subarray auf, sodass es in [47, 56, 98] sortiert wird.

Schließlich werden die Subarrays kombiniert, um das sortierte Array zu erhalten – [3, 6, 7, 11, 47, 56, 98].

Implementierung

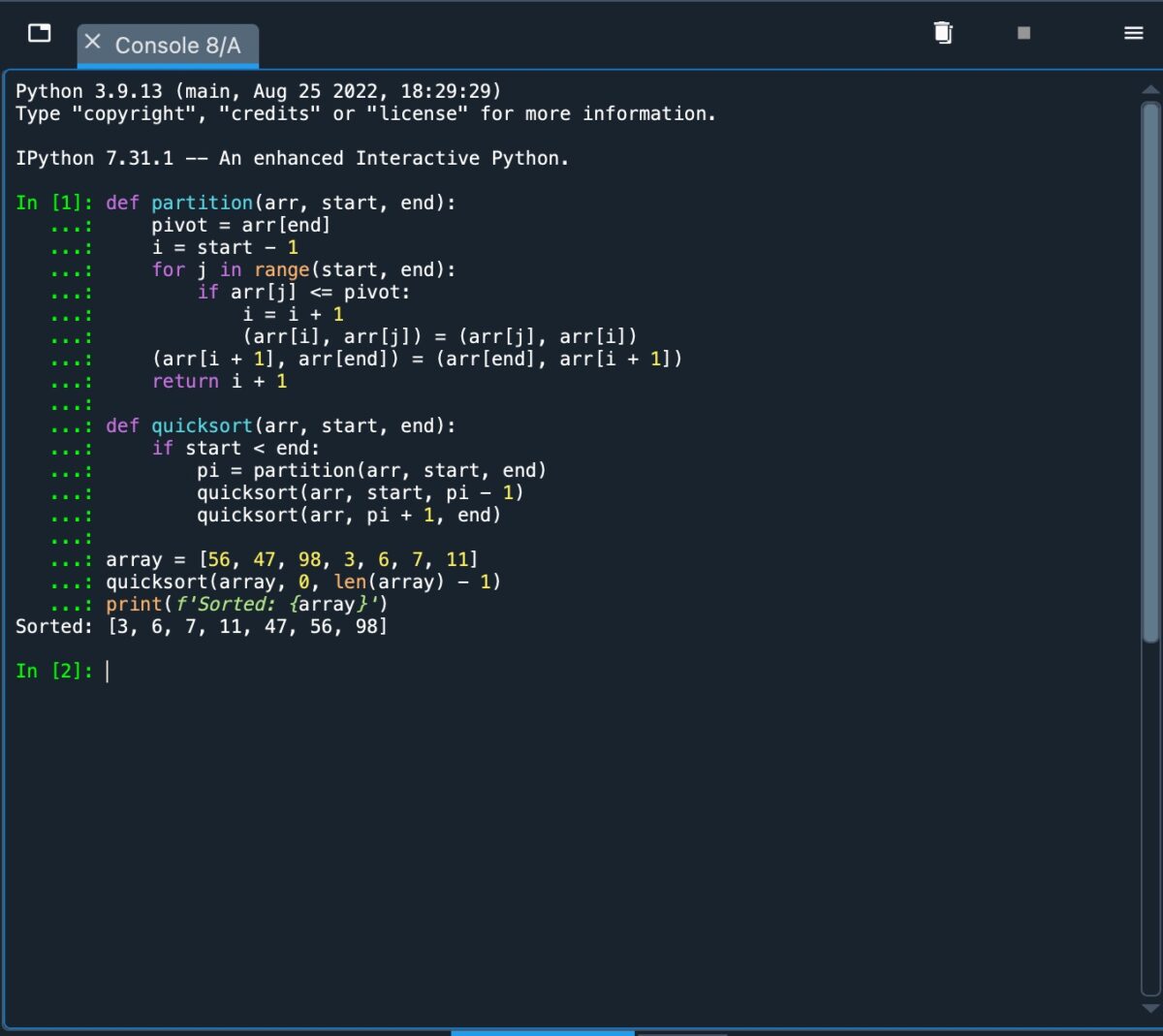
Nun haben wir die Grundlagen hinter Quick Sort behandelt, implementieren wir es mit Python. Der von uns verwendete Code kann wie folgt beschrieben werden:

def partition(arr, start, end): pivot=arr[end] i=start-1 for j in range(start, end): if arr[j]=Drehpunkt: i=i + 1 (arr[i], arr[j]=(arr[j], arr[i]) (arr[i + 1], arr[ende])=(arr[ende], arr[i + 1]) return i + 1 def quicksort(arr, start, end): if start end: pi=partition(arr, start, end) quicksort(arr, start, pi-1) quicksort(arr, pi + 1, end) array=[56, 47, 98, 3, 6, 7, 11] quicksort(array, 0, len(array)-1) print(f’Sorted: {array}’)

First , definieren wir eine Partitionsfunktion als Funktion eines Arrays mit einem Anfangs-und Endindex.

Der Pivot-Wert wird dann auf das letzte Element des Arrays gesetzt und i wird mit dem Anfang initialisiert index, minus 1.

Die „for“-Schleife durchläuft das Array, vom Startindex bis zum Endindex minus 1.

Die „if“-Anweisung tauscht das aktuelle Element aus, j, mit dem Wert am Index i, wenn j kleiner als oder Gl ual zum Drehpunkt. Anschließend wird die Variable i inkrementiert.

Danach wird der Pivot mit dem Element am Index i+1 vertauscht. Das bedeutet, dass alle Elemente links vom Pivot kleiner oder gleich diesem sind und Elemente rechts größer als er.

Danach wird der Index des Pivot-Werts zurückgegeben.

„Quicksort“ wird dann als Funktion des Arrays definiert, und das Array wird überprüft, ob es mehr als ein Element enthält.

Dann wird die Funktion „partition“ mit dem Index aufgerufen Wert auf „pi“ gesetzt. Quicksort wird rekursiv auf dem linken und rechten Subarray aufgerufen, bis jedes Subarray nur noch ein Element enthält.

Schließlich wird ein sortiertes Array erstellt und mit der „print“-Funktion ausgedruckt.

Quick Sort wird links rekursiv aufgerufen und richtige Subarrays, bis jedes Subarray nur noch ein Element enthält.

©”TNGD”.com

Beste und schlechteste Anwendungsfälle von Quick Sort

Während die Theorie hinter Quick Sort möglicherweise auf den ersten Blick kompliziert erscheinen, hat der Algorithmus viele Vorteile und ist im Allgemeinen recht schnell. Werfen wir einen Blick auf die Zeit-und Raumkomplexität von Quick Sort.

Zeitkomplexität von Quick Sort

Die Tabelle fasst die Zeitkomplexität von Quick Sort zusammen.

CaseTime ComplexityBestO (n log n)AverageO (n log n)WorstO (n2)

Der beste Fall ist, wenn die Partition ausgeglichen ist, wobei der Pivot nahe oder gleich dem Medianwert ist. Als solche haben beide Subarrays eine ähnliche Größe, und auf jeder Ebene werden n Operationen durchgeführt. Dies führt zu einer logarithmischen Zeitkomplexität.

Wenn das Pivot-Element relativ nahe ist, ist dies der durchschnittliche Fall. Die Zeitkomplexität ist die gleiche wie im besten Fall, da die Arrays ungefähr gleich groß sind.

Der schlimmste Fall verwandelt die Zeitkomplexität jedoch in quadratische Zeit. Dies liegt daran, dass das Array sehr unausgeglichen ist, wobei der Drehpunkt nahe am minimalen oder maximalen Element liegt. Dies führt zu einer Situation, in der die Subarrays sehr ungleichmäßig groß sind, wobei eines nur ein Element enthält. Als solches gibt es n Rekursionsebenen sowie n Operationen, was zu einer quadratischen Abhängigkeit von der Eingabegröße führt.

Platzkomplexität der Schnellsortierung

Ein weiterer zu berücksichtigender Faktor ist der Platz Komplexität der schnellen Sorte. Dies kann wie folgt zusammengefasst werden:

Die Platzkomplexität für die schnelle Sortierung ist für Best und Average gleich Fälle. Dies liegt daran, dass der Algorithmus log n rekursive Ebenen hat und jeder rekursive Aufruf eine konstante Menge an Speicherplatz verwendet. Somit ist der gesamte Speicherplatz proportional zur Tiefe des Rekursionsbaums.

Im schlimmsten Fall ändert sich die Speicherplatzkomplexität jedoch auf O(n). Weil der Rekursionsbaum erheblich unausgeglichen ist, was bedeutet, dass es n rekursive Aufrufe gibt.

Zusammenfassung

Insgesamt ist die schnelle Sortierung, wie der Name schon sagt, eine sehr effiziente Art, eine zu sortieren Array, besonders große. Sobald der Prozess verstanden ist, ist er relativ einfach zu implementieren und zu ändern. Es ist in einer Vielzahl von Szenarien nützlich und dient als gute Grundlage für komplexere Sortieralgorithmen.

Als Nächstes …

Was ist Quick Sort und wie funktioniert es? (Mit Beispielen) FAQs (Häufig gestellte Fragen) 

Was ist Schnellsortierung?

Schnellsortierung ist ein Sortieralgorithmus zum Sortieren von Datenarrays. Es funktioniert, indem ein Pivot-Element ausgewählt und das Array in zwei Subarrays aufgeteilt wird, eines mit kleineren Elementen als der Pivot und eines mit größeren Elementen. Dieser Vorgang wird rekursiv wiederholt, bis jedes Subarray sortiert ist und nur noch ein Element enthält. Die Arrays werden dann zu einem sortierten Array kombiniert.

Ist Quick Sort ein stabiler Algorithmus?

Quick Sort ist normalerweise ein instabiler Algorithmus. Das bedeutet, dass die relative Reihenfolge gleicher Elemente in der endgültigen Ausgabe möglicherweise nicht erhalten bleibt.

Wie wählen Sie das Pivot-Element mit Schnellsortierung aus?

Sie können entweder das erste oder das letzte Element auswählen oder eine zufällige Auswahl treffen. Bei besonders großen Datensätzen führt eine Randomisierung der Auswahl im Allgemeinen zu einer guten Leistung.

Wie hoch ist die zeitliche Komplexität von Quick Sort?

Der beste und durchschnittliche Fall ist O(n log n), während der schlimmste Fall O(n2) ist.

Wie groß ist die Raumkomplexität von Quick Sort?

Das Beste und durchschnittliche Fälle sind O(log n), wohingegen der schlimmste Fall O(n) ist.

Was sind die besten Fälle für die Verwendung von Schnellsortierung?

Quick Sort kann für viele Arten von Arrays verwendet werden, aber manchmal funktionieren Alternativen wie Heap-Sort oder Merge-Sort unter bestimmten Bedingungen besser. Dies ist normalerweise der Fall, wenn Sie einen stabilen Algorithmus wie Mergesort benötigen oder wenn Zeit ein Faktor ist. Zum Beispiel ist die Zeitkomplexität für den ungünstigsten Fall der Heap-Sortierung so gut wie die durchschnittliche Zeitkomplexität für die schnelle Sortierung. Einfachere Algorithmen wie Selection oder Insertion Sort können auch für kleine Datasets schneller sein.