© metamorworks/Shutterstock.com
Beim Sortieren einer Reihe von Daten ist es wichtig, sich mit Sortieralgorithmen vertraut zu machen. In Datenstrukturen ordnet das Sortieren Daten in einem bestimmten Format an, basierend auf einer linearen Beziehung zwischen Datenelementen.
Das Sortieren ist unerlässlich, da die Datensuche auf einem sehr hohen Niveau optimiert werden kann, wenn die Daten in einem bestimmten Format sortiert werden. Darüber hinaus kann das Sortieren Daten in einem besser lesbaren Format darstellen. Wir haben eine große Auswahl an Sortieralgorithmen, aber in diesem Artikel werden wir untersuchen, was Heap-Sortierung ist und wie man sie verwendet. Fangen wir gleich an!

Was ist Heap Sort: Eine genaue Definition
Heap Sort ist ein bekannter und effizienter Sortieralgorithmus. Es ist ein Konzept, das verwendet wird, um Array-Daten zu sortieren, indem Elemente eines nach dem anderen aus dem Haufen entfernt werden – ein vollständiger binärer Baum – Teil der Liste, und sie dann in den sortierten Teil der Liste einfügen.
Heap-Sortierung im Grunde umfasst zwei Phasen:
Erstellen eines Heaps, entweder Max-Heap oder Min-Heap, unter Verwendung von Elementen eines angegebenen Arrays. Rekursives Löschen des Wurzelelements des in der ersten Phase erstellten Heaps.
Wie funktioniert der Heap-Sortieralgorithmus?
So wird der Heap-Sortieralgorithmus implementiert:
Erstellen Sie einen maximalen Heap, um Daten aus der unsortierten Liste zu speichern. Nehmen Sie den größten Wert heraus den Heap und fügen Sie ihn in eine sortierte Liste ein. Tauschen Sie die Wurzel des Heaps mit dem letzten Element in der Liste aus und gleichen Sie den Heap dann neu aus. Sobald der Max-Heap vollständig leer ist, geben Sie die sortierte Liste zurück.
Hier ist der Algorithmus
HeapSort(arr)
CreateMaxHeap(arr)
for i=length(arr) bis 2
arr[1] mit arr[i] tauschen
heap_size[arr]=heap_size[arr] ? 1
MaxHeapify(arr,1)
Ende
Sehen wir uns die Schritte etwas genauer an.
Schritt 1: Erstellen Sie eine max-heap
CreateMaxHeap(arr)
heap_size(arr)=length(arr)
for i=length(arr)/2 to 1
MaxHeapify(arr,i)
Ende
In diesem Algorithmus müssen wir einen Max-Heap aufbauen. Wie wir alle wissen, ist der größte Wert in einem Max-Heap der Wurzelwert. Jeder übergeordnete Knoten muss einen größeren Wert haben als seine zugehörigen untergeordneten Knoten.
Stellen Sie sich vor, wir hätten die folgende Liste unsortierter Werte:
[14, 11, 2, 20, 3, 10 , 3]
Indem wir unsere Werte in eine Max-Heap-Datenstruktur einfügen, würde unsere Liste so aussehen:
[20, 11, 14, 2, 10, 5 , 3]
Wir können den obigen Max-Heap so darstellen:
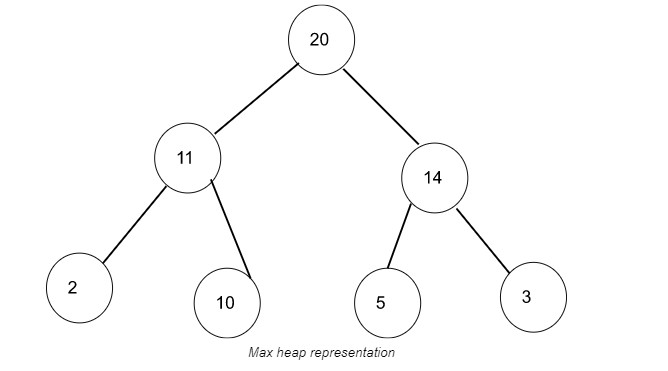 Darstellung eines Max-Heaps.
Darstellung eines Max-Heaps.
©”TNGD”.com
Schritt 2: Entfernen Sie die Wurzel des Heaps
Um die Daten zu sortieren, extrahieren und entfernen wir wiederholt den größten Wert aus dem Heap, bis er leer ist. Wenn wir den Prinzipien von Heaps folgen, können wir davon ausgehen, dass sich der größte Wert an der Heap-Wurzel befinden wird.
Nachdem wir den größten Wert eliminiert haben, können wir den Heap nicht einfach ohne Wurzel verlassen, da dies der Fall ist würde dazu führen, dass zwei Knoten getrennt werden. Stattdessen können wir den Wurzelknoten mit dem letzten Element im Heap austauschen. Da das letzte Element keine Kinder hat, kann es leicht aus dem Heap entfernt werden.
Dieser Schritt verursacht jedoch ein großes Problem. Durch das Vertauschen der beiden Elemente ist der Wurzelknoten jetzt nicht der größte im Heap. Der Heap muss umstrukturiert werden, um sicherzustellen, dass er ausgeglichen ist.
Schritt 3: Herunter stapeln (den Heap wiederherstellen)
Der Wurzelwert ist nicht der größere Wert, das Heap-Prinzip war es verletzt, da der Elternwert einen Wert haben muss, der größer ist als der Wert der Kinder.
Es gibt jedoch eine Lösung für dieses Problem! Wir müssen aufhäufen, was bedeutet, dass Sie am Ende des Haufens einen Wert hinzufügen und sich in der Datenstruktur nach oben arbeiten, bis Sie die richtige Position gefunden haben. Zum Verringern vergleichen Sie den neuen Wurzelwert mit seinen Kindern, wählen das Kind mit dem größeren Wert aus und tauschen es mit dem Wurzelwert aus. Arbeite dich den Haufen nach unten, bis er ausgeglichen ist.
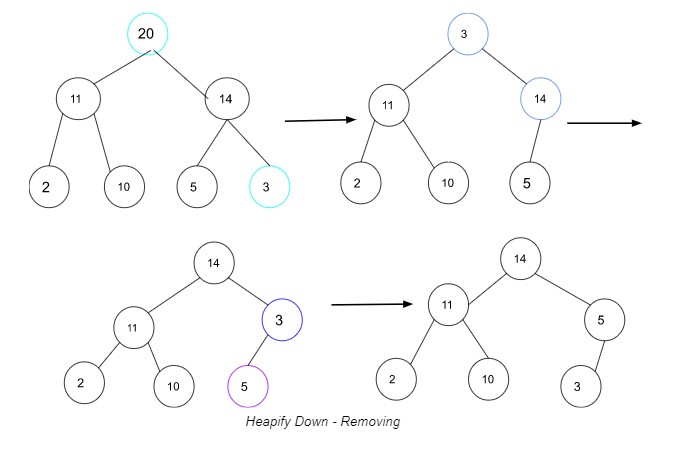 Darstellung des Heapify-Down-Prozesses.
Darstellung des Heapify-Down-Prozesses.
©”TNGD”.com
Im obigen Beispiel tauschen Sie den ursprünglichen Wurzelwert 20 mit 3 aus – dem Kind ganz rechts. Wenn Sie 3 als neuen Stamm haben, vergleichen Sie seinen Wert mit seinem untergeordneten Wert 14, und da er größer als 3 ist, tauschen Sie sie aus, um 14 zum neuen Stamm zu machen. Vergleichen Sie als Nächstes 3 mit dem neuen untergeordneten Wert 5, und da 5 größer als 3 ist, tauschen Sie sie aus, sodass 5 der neue übergeordnete Wert ist. Da es keine anderen Kinder gibt, die mit 3 verglichen werden können, ist der Haufen jetzt ausgeglichen.
Schritt 4: Wiederholen
Sie müssen den Vorgang des Vertauschens der Wurzel und der letzten wiederholen Element, den größten Wert herausnehmen und den Heap neu ausgleichen, solange die Datenstruktur eine Größe größer als 1 enthält. Wenn dieses Kriterium erfüllt ist, haben Sie einen sortierten Satz von Werten.
Heap-Sortierungskomplexität
Zeitkomplexität
Hier ist die Zeitkomplexität von Heap Sort im besten Fall, durchschnittlichen Fall und schlimmsten Fall.
Best Case Complexity: Tritt auf, wenn das Array bereits sortiert ist, d. h. keine Sortierung erforderlich ist. O(n log n) ist die optimale Zeitkomplexität der Heap-Sortierung. Durchschnittliche Fallkomplexität: Tritt auf, wenn die Elemente im Array nicht in korrekt aufsteigender oder absteigender Reihenfolge angeordnet sind, was zu a führt durcheinandergebrachte Reihenfolge. O(n log n) ist die durchschnittliche Case-Time-Komplexität der Heap-Sortierung. Worst-Case-Komplexität: Dies geschieht, wenn Sie die Array-Elemente in umgekehrter Reihenfolge sortieren müssen, d. h. wenn die Elemente anfänglich in absteigender Reihenfolge sind Reihenfolge müssen Sie sie in aufsteigender Reihenfolge sortieren. O(n log n) ist die Worst-Case-Zeitkomplexität der Heap-Sortierung.
Raumkomplexität
Die Raumkomplexität von Heap Sort ist O(1)
Wie wird der Heap-Sortierungsalgorithmus implementiert?
So wird Heap-Sortierung in der Java-Programmiersprache implementiert.
//Um einen Unterbaum zu häufen. Hier ist „i“ der Root-Node-Index in arr[] und „x“ die Heap-Größe
public class HeapSort {
public static void sort(int[] arr) {
int x=arr.length;
//Array neu anordnen (Heap erstellen)
for (int i=x/2 – 1; i >=0; i–)
heapify(arr, x, i);
//Elemente einzeln aus dem Heap extrahieren
for (int i=x – 1; i > 0; i–) {
//Anfangswurzel ans Ende verschieben
int temp=arr[0];
arr[0]=arr[i];
arr[i]=temp;
//Aufruf der Max-Heapify-Funktion auf dem reduzierten Heap
heapify(arr, i, 0);
}
}
static void heapify(int[] arr, int x, int i) {
int größte=i;//Größten als Wurzel initialisieren
int l=2 * i + 1;//links
int r=2 * i + 2;//rechts
//wenn das linke Kind größer als die Wurzel ist
if (l x && arr[l] > arr[größte])
größte=l;
//wenn das rechte Kind größer als das bisher größte ist
if (r x && arr[r] > arr[größte])
größte=r;
//wenn größte nicht die Wurzel ist
if (größte !=i){
int swap=arr[i];
arr[i]=arr[größte];
arr[größte]=tauschen;
//den betroffenen Unterbaum wiederholt häufen
heapify(arr, x, large);
}
}
//eine Funktion zum Drucken eines Arrays der Größe x
static void printArray(int[]) {
int x=arr.length;
for (int i=0; i x; ++i)
System.out.print(arr[i] + ” “);
System.out.println();
}
//Treibercode
public static void main (String[] args) {
int[] arr={ 13, 12, 14, 6, 7, 8 };
sort(arr);
System.out.println(“Sortiertes Array ist”);
printArray(arr);
}
}
Ausgabe
Dies ist das sortierte Integer-Array in aufsteigender Reihenfolge.
Das sortierte Array ist
6, 7, 8, 12, 13, 14
Vor-und Nachteile des Heap-Sortieralgorithmus
Vorteile
Effizienz: Dieser Sortieralgorithmus ist sehr effizient, da die zum Sortieren eines Haufens benötigte Zeit logarithmisch zunimmt, während bei anderen Algorithmen die Zeit exponentiell langsamer wächst, wenn die Sortierelemente zunehmen.Einfachheit: Im Vergleich zu anderen ebenso effizienten Algorithmen ist es einfacher, da es keine fortschrittlichen Informatikprinzipien wie Rekursion verwendet. Speichernutzung: Heap-Sortierung verwendet minimalen Speicher, um die anfängliche Liste der zu sortierenden Elemente zu speichern , und es wird kein zusätzlicher Speicherplatz benötigt, um zu funktionieren.
Nachteile
Teuer: Heap-Sortierung ist kostspielig.Instabil: Heap-Sortierung ist unzuverlässig, da sie die relevante Reihenfolge der Elemente ändern könnte.Ineffizient: Beim Umgang mit hochkomplexen Daten ist Heap Sort nicht sehr effizient.
Anwendungen der Heap-Sortierung
Möglicherweise sind Sie auf den Algorithmus von Dijkstra gestoßen, der Heap-Sortierung verwendet, um den kürzesten Pfad zu bestimmen. In der Datenstruktur ermöglicht die Heap-Sortierung das schnelle Abrufen entweder des kleinsten (kürzesten) oder größten (längsten) Werts. Es hat verschiedene Anwendungen, darunter das Bestimmen der Reihenfolge in Statistiken, das Verwalten von Prioritätswarteschlangen in Prims Algorithmus (auch bekannt als Minimum Spanning Tree) und das Durchführen von Huffman-Codierung oder Datenkomprimierung.
Ebenso verwenden verschiedene Betriebssysteme den Heap Sortieralgorithmus für Auftrags-und Prozessmanagement, da er auf einer Prioritätswarteschlange basiert.
In einem realen Szenario kann Heap Sort in einem SIM-Kartengeschäft angewendet werden, wo wir eine lange Warteschlange von Kunden haben warten darauf, bedient zu werden. Die Kunden, die ihre Rechnungen bezahlen müssen, können priorisiert werden, da ihre Arbeit nur minimale Zeit in Anspruch nimmt. Dieser Ansatz spart vielen Kunden Zeit und vermeidet unnötige Verzögerungen, was zu einer effizienteren und zufriedenstellenderen Erfahrung für alle führt.
Zusammenfassung
Jeder Sortier-oder Suchalgorithmus hat seine Vor-und Nachteile , und Heap Sorting ist keine Ausnahme. Die Heap-Sort-Nachteile sind jedoch relativ gering. Zum Beispiel benötigt es keinen zusätzlichen Speicherplatz über den bereits zugewiesenen Speicherplatz hinaus.
Zeit ist ein weiterer Faktor. Es wurde festgestellt, dass die Zeitkomplexität unter Verwendung von nlog(n) bestimmt wird, aber die tatsächliche Haufensortierung kleiner als O(nlog(n)) ist. Dies liegt daran, dass die Extraktion aus der Haufensortierung die Größe reduziert und somit weniger Zeit in Anspruch nimmt, während der Prozess fortschreitet. Daher wird Heap Sort aus verschiedenen Gründen weithin als einer der „besten“ Sortieralgorithmen im Bereich der Datenstruktur angesehen.
Was ist Heap Sort und wie wird es verwendet? FAQs (Frequently Asked Questions)
Was ist mit Heapify gemeint?
Heapify ist der Prozess des Aufbaus einer Heap-Datenstruktur aus einer Array-Darstellung einer Binärdatei Baum. Dieser Prozess kann verwendet werden, um entweder einen Max-Heap oder einen Min-Heap zu erstellen. Es beginnt mit dem letzten Index des Nicht-Blatt-Knotens im Binärbaum, dessen Index durch n/2 – 1 gegeben ist. Heapify wird durch Rekursion implementiert.
Wie funktioniert Heap Sort?
Heapsort ist ein vergleichsbasierter Sortieralgorithmus. Es funktioniert, indem die größten Elemente aus dem unsortierten Bereich in den sortierten Bereich verschoben werden, wodurch der unsortierte Bereich verkleinert wird. Heap Sort visualisiert die Elemente des Arrays als Heap und ist bekannt für seine optimale Laufzeit. Dieser Algorithmus ist nützlich, wenn Sie die Ordnung aufrechterhalten möchten, während Sie das minimale oder maximale Element aus dem Array extrahieren.
Wie „häufen“ Sie einen Baum?
Um einen Binärbaum umzugestalten oder zu stapeln, wählen Sie zunächst einen Knoten als Wurzelknoten des Teilbaums aus. Anschließend vergleichen Sie den Wert des Stammknotens mit den Werten seiner linken und rechten untergeordneten Knoten. Wenn einer der untergeordneten Knoten einen größeren (bei einem maximalen Heap) oder einen kleineren (bei einem minimalen Heap) Wert als der Stammknoten hat, tauschen Sie die Werte des Stammknotens und des untergeordneten Knotens mit aus der größere (oder kleinere) Wert. Nachdem Sie die Werte ausgetauscht haben, häufen Sie rekursiv den Teilbaum, der am untergeordneten Knoten verwurzelt ist, bis der gesamte Teilbaum die Heap-Eigenschaft erfüllt. Sie wiederholen diesen Vorgang für jeden Knoten im Baum, bis der gesamte Baum die Heap-Eigenschaft erfüllt.
Die Zeitkomplexität von Heapify ist O(log n), wobei n die Anzahl der Knoten im Unterbaum ist, die geheapft werden.
Was ist ein binärer Heap?
Ein binärer Heap ist eine Datenstruktur, die als vollständiger binärer Baum betrachtet werden kann, in dem sich alle übergeordneten Knoten befinden kleiner oder gleich seinen Kindern (in einem Min-Heap) oder größer oder gleich seinen Kindern (in einem Max-Heap).
Was sind die Vorteile der Heap-Sortierung?
Zu den Vorteilen der Heap-Sortierung gehört die zeitliche Komplexität von O(n log n), die schneller ist als einige andere gängige Sortieralgorithmen wie Bubble Sort und Insertion Sort. Darüber hinaus hat Heap-Sortierung einen geringen Speicherbedarf, da sie nur konstant zusätzlichen Speicherplatz benötigt.
Was sind die Nachteile von Heap-Sortierung?
Die Zu den Nachteilen der Heap-Sortierung gehört ihre instabile Sortiereigenschaft, was bedeutet, dass die relative Reihenfolge gleicher Elemente nach dem Sortieren möglicherweise nicht erhalten bleibt. Darüber hinaus ist die Heap-Sortierung für kleine Arrays nicht sehr effizient, und ihre rekursive Natur kann auf einigen Architekturen zu einer langsameren Leistung führen.