© pinkeyes/Shutterstock.com
Dijkstras Algorithmus ist nur ein Beispiel dafür, was wir einen Shortest-Path-Algorithmus nennen. Kurz gesagt, dies sind Algorithmen, die verwendet werden, um die kürzeste Entfernung (oder den kürzesten Pfad) zwischen Scheitelpunkten eines Diagramms zu finden.
Während der kürzeste Weg auf verschiedene Arten definiert werden kann, wie z. B. Zeit, Kosten oder Entfernung, bezieht er sich normalerweise auf die Entfernung zwischen Knoten. Wenn Sie mehr darüber erfahren möchten, wie der Algorithmus von Dijkstra funktioniert und wofür Sie ihn verwenden können, sind Sie hier genau richtig.

Was ist der Dijkstra-Algorithmus?
Einfach ausgedrückt ist der Dijkstra-Algorithmus eine Methode, um die kürzester Weg zwischen Knoten in einem Graphen. Ein Quellknoten wird bestimmt, und dann wird die Entfernung zwischen diesem Knoten und allen anderen Knoten unter Verwendung des Algorithmus berechnet.
Im Gegensatz zu einigen anderen Shortest-Path-Algorithmen kann der von Dijkstra nur mit nicht-negativ gewichteten Graphen arbeiten. Das heißt, Diagramme, in denen der Wert jedes Knotens eine Menge darstellt, wie z. B. Kosten oder Entfernung, und alle Werte positiv sind.
Der Algorithmus
Bevor wir uns mit der Implementierung des Dijkstra-Algorithmus befassen Code, lassen Sie uns die beteiligten Schritte durchgehen:
Zuerst initialisieren wir eine leere Prioritätswarteschlange; nennen wir das „Q“. Dies ist die effizienteste Art, den Algorithmus zu verwenden, da er sicherstellt, dass wir immer den nächstgelegenen Scheitelpunkt zum Quellknoten auswählen. Da wir die Abstände von jedem Scheitelpunkt zum Quellknoten noch nicht kennen, initialisieren wir alle Scheitelpunktabstände bis unendlich. Der Abstand des Quellknotens oder Quellknotens wird ebenfalls auf 0 gesetzt, da dies unser Startpunkt ist. Der Quellknoten wird dann mit einer Priorität von 0 zur Prioritätswarteschlange hinzugefügt. Zu Beginn der Knoten mit dem kleinsten Entfernung wird aus der Warteschlange entfernt. Dieser Scheitelpunkt wird „u“ genannt, und benachbarte Scheitelpunkte werden mit „v“ bezeichnet. Der Abstand vom Quellknoten zu jedem v bis u wird berechnet, und wenn der Abstand kleiner als der aktuelle Abstand zu v ist, wird der Abstand aktualisiert. Sobald v berechnet ist, wird dies in die Prioritätswarteschlange eingefügt, wobei seine Priorität auf gesetzt ist entspricht seinem Abstand vom Quellscheitelpunkt. Dadurch wird sichergestellt, dass Scheitelpunkte mit kleineren Abständen zuerst priorisiert werden, wodurch die Effizienz des Algorithmus aufrechterhalten wird, indem zuerst die nächstgelegenen, nicht besuchten Scheitelpunkte berücksichtigt werden.
Funktionsweise des Dijkstra-Algorithmus
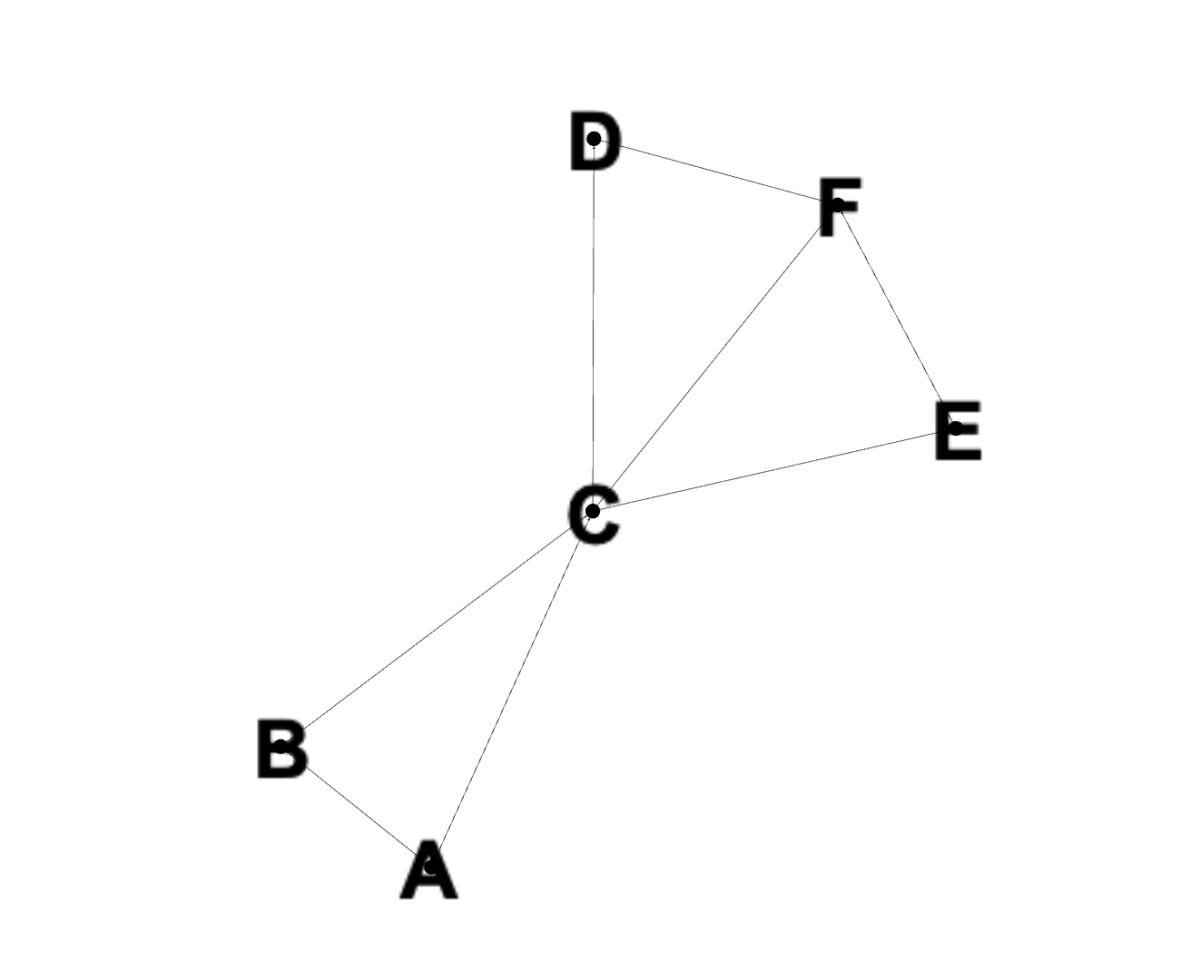 Vertices A bis F.
Vertices A bis F.
©”TNGD”.com
Nun, da wir die Grundlagen des Dijkstra-Algorithmus behandelt haben, wollen wir uns anhand eines Beispiels ansehen, wie er funktionieren würde. Nehmen Sie zuerst einen Graphen mit Knoten, die wie folgt angeordnet sind:
Wir haben Knoten A bis F, die durch verschiedene Pfade miteinander verbunden sind. Diese Verbindungen werden auch als Kanten bezeichnet. Wenn wir A als unseren Startknoten wählen, werden alle Pfadwerte für die anderen Knoten auf unendlich gesetzt, wie zuvor besprochen.
Wir gehen dann zu jedem Knoten und aktualisieren seine Pfadlänge. Wenn der berechnete Abstand zum benachbarten Knoten kleiner ist als der aktuelle Abstand zu diesem Scheitelpunkt, wird der Abstand aktualisiert.
Wenn wir die Priorität jedes Scheitelpunkts gleich seiner Entfernung von der Quelle setzen, vermeiden wir, dass Knoten zweimal besucht werden. Beim Besuch eines nicht besuchten Knotens wählen wir zuerst die kürzeste Pfadlänge. Dieser Prozess wird wiederholt, bis jeder Knoten besucht wurde und die Entfernung vom Quellknoten berechnet wurde.
Implementierung des Dijkstra-Algorithmus unter Verwendung eines Haufens
Es ist Zeit, etwas Code für den Dijkstra-Algorithmus zu implementieren in Python und sehen, wie das funktioniert. Wir beginnen mit einer einfachen Implementierung einer Prioritätswarteschlange, die als Heap bezeichnet wird. Der Code kann wie folgt dargestellt werden:
import heapq import sys def dijkstra_heap(adj_matrix, source): num_vertices=len(adj_matrix) distances=[sys.maxsize] * num_vertices distances[source]=0 visited=[False] * num_vertices heap=[(0, source)] while heap: current_distance, current_vertex=heapq.heappop(heap) visited[current_vertex]=True für Neighbor_vertex in range(num_vertices): weight=adj_matrix[current_vertex][neighbor_vertex] falls nicht besucht [neighbor_vertex] and weight !=0: distance=current_distance + weight if distance distances[neighbor_vertex]: distances[neighbor_vertex]=distance heapq.heappush(heap, (distance, Neighbor_vertex)) return distances adj_matrix=[ [0, 2, 2 , 0, 0, 0], [2, 0, 2, 0, 0, 0], [2, 2, 0, 2, 2, 6], [0, 0, 2, 0, 2, 2], [0, 0, 2, 2, 0, 2], [0, 0, 6, 2, 2, 0] ] Abstände=dijkstra_heap(adj_matrix, 0) print(di stances)
Erklärung des Codes
Lassen Sie uns diesen Code Schritt für Schritt aufschlüsseln, damit wir verstehen können, was vor sich geht.
Module importieren
Zunächst importieren wir die Module „heapq“ und „sys“. Das erste Modul erlaubt uns, die Heap-Datenstruktur zu verwenden, während das zweite uns erlaubt, den maximalen ganzzahligen Wert zu verwenden. Dies ist erforderlich, weil wir die Scheitelpunktabstände auf unendlich initialisieren.
Definieren des Dijkstra-Algorithmus
Als Nächstes definieren wir „dijkstra_heap“ als eine Funktion mit zwei Argumenten – „adj_matrix“ und „ Quelle”. Dies sind eine Darstellung des Graphen als Adjazenzmatrix bzw. der Index des Quellknotens.
Besuch der Knoten
In diesem Block berechnen wir die Anzahl der Knoten. Dann initialisieren wir die Entfernungen vom Quellscheitelpunkt zu jedem Zielscheitelpunkt auf unendlich, wie zuvor erwähnt. Der Abstand des Quellknotens wird ebenfalls auf Null gesetzt.
Dann wird eine Liste namens „visited“ erstellt, die auf „False“ initialisiert wird. Das bedeutet, dass Knoten zunächst als unbesucht gelten, bis wir die Entfernung zwischen ihnen und der Quelle berechnet haben. Eine Prioritätswarteschlange namens „Heap“ wird ebenfalls erstellt, wobei der Anfangspunkt und die Entfernung vom Quellknoten als Tupel bezeichnet werden.
Aktualisieren der kürzesten Pfadlängen
Als Nächstes wir haben eine „while“-Schleife, die läuft, bis die Warteschlange leer ist. Die erste Zeile nimmt den Scheitelpunkt von dem Haufen, der die kürzeste Entfernung vom Quellscheitelpunkt hat, und die zweite Zeile markiert den Scheitelpunkt als besucht, sobald dieser Abstand berechnet ist.
Wir folgen dem mit einer „for“-Schleife , die über alle Nachbarn des Knotens, mit dem wir uns gerade beschäftigen, iteriert. Das Gewicht jeder Kante wird abgerufen, und es wird geprüft, ob Nachbarknoten besucht wurden und ob die Gewichte nicht Null sind. Die Entfernung zum Nachbarknoten wird dann anhand der Entfernung von der Quelle zum aktuellen Knoten berechnet.
Wir haben eine weitere „if“-Anweisung, die prüft, ob die berechnete Entfernung kürzer ist als die aktuell kürzeste Entfernung in unserem Liste „Entfernungen“. Wenn dies der Fall ist, aktualisiert die nächste Zeile diesen Wert. Schließlich wird der benachbarte Vertex, sowie seine Entfernung von der Quelle, zum Heap hinzugefügt.
Ergebnisausgabe
Nachdem dieser Vorgang abgeschlossen ist, werden die Entfernungen vom Quellknoten zu alle anderen Knoten im Diagramm werden an die Konsole zurückgegeben.
Der vorletzte Codeblock stellt einfach das Diagramm dar, das wir uns als Adjazenzmatrix ansehen, wobei der Wert in Zelle {i, j} die darstellt Gewicht der Kante, die die beiden Scheitelpunkte verbindet.
Der letzte Code weist das System einfach an, die kürzesten Pfadabstände zu berechnen und diese dann auf der Konsole auszugeben.
Implementierung des Codes
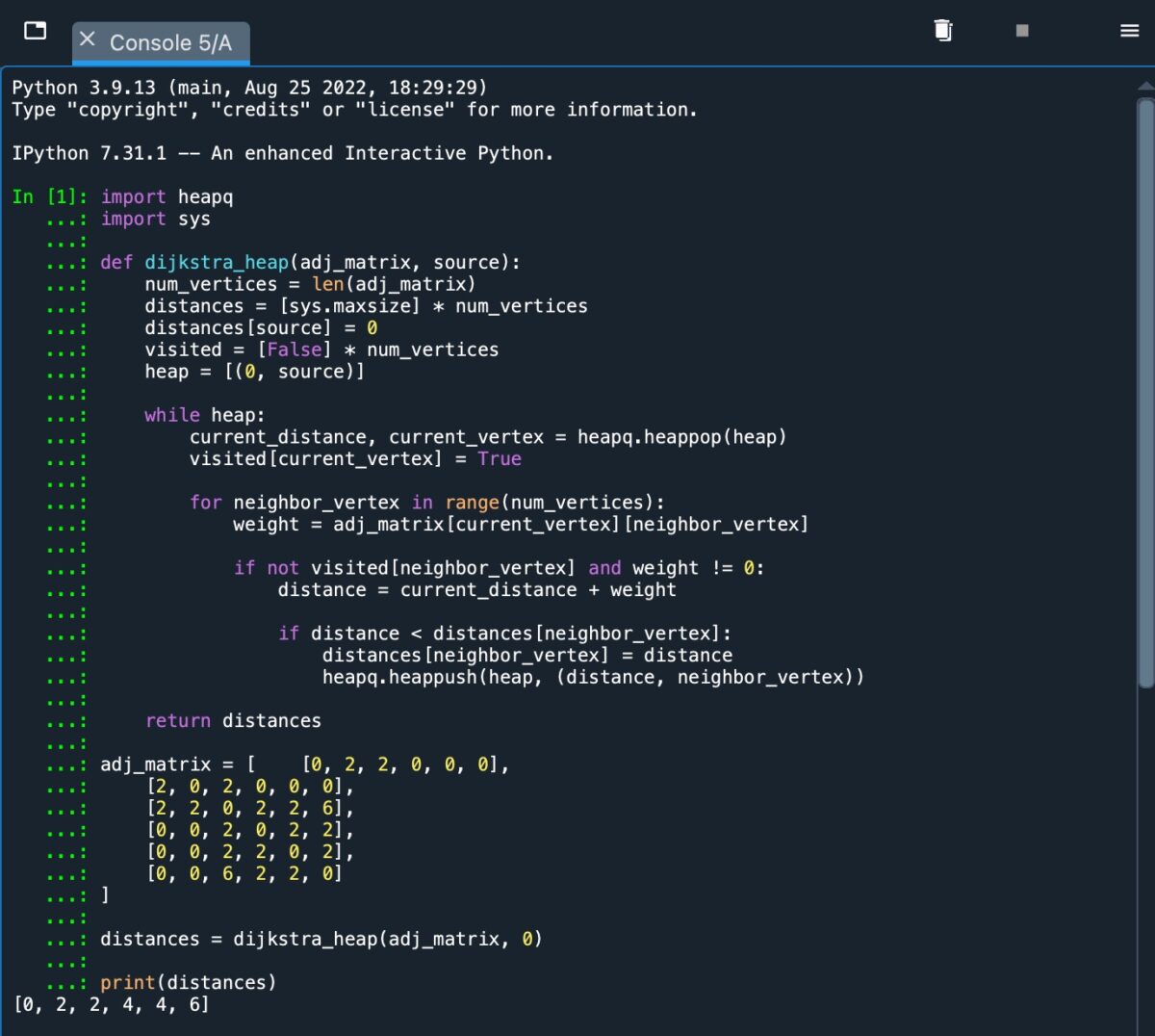 Die einfache Implementierung einer heap.
Die einfache Implementierung einer heap.
©”TNGD”.com
Wie wir auf dem Screenshot sehen können, erhalten wir eine Ausgabe von [0, 2, 2, 4, 4, 6], was die kürzeste Pfadentfernung darstellt vom Quellknoten A zu den Knoten B, C, D, E und F.
Beste und schlechteste Verwendung Fälle des Dijkstra-Algorithmus
Im Allgemeinen wird der Dijkstra-Algorithmus als effizient angesehen, obwohl einige Algorithmen in speziellen Fällen möglicherweise besser abschneiden. Betrachten wir nun die zeitliche und räumliche Komplexität des Dijkstra-Algorithmus im besten, durchschnittlichen und ungünstigsten Fall.
Zeitkomplexität des Dijkstra-Algorithmus
Normalerweise wir haben nur eine Komplexität für jeden Fall. Aber mit Dijkstras Algorithmus ist die Situation nicht so eindeutig. Dies liegt daran, dass Sie den Algorithmus auf verschiedene Arten implementieren können, hauptsächlich durch die Verwendung einer Prioritätswarteschlange.
Wenn Sie eine Prioritätswarteschlange verwenden, können Sie entweder eine binäre Heap-Methode oder eine Fibonacci-Heap-Methode verwenden. Im Allgemeinen führt der Fibonacci-Heap zu einer effizienteren Leistung und einer besseren Worst-Case-Zeitkomplexität von O((E + V) log V), wobei E die Anzahl der Kanten und V die Anzahl der Eckpunkte ist.
Wenn Sie keine Prioritätswarteschlange verwenden und der Graph dicht ist, könnte die Komplexität im ungünstigsten Fall so ineffizient wie O(V2 log V) sein.
Bezogen auf den Durchschnittsfall , ist die zeitliche Komplexität etwas günstiger. Der durchschnittliche Fall bezieht sich darauf, wenn eine Prioritätswarteschlange verwendet wird, um die Mindestentfernungen zu jedem Scheitelpunkt zu berechnen.
Der beste Fall ist streng genommen ein ungewöhnlicher. Sie würden sich wahrscheinlich nicht die Mühe machen, den Algorithmus zu verwenden, um es zu lösen. Dies liegt daran, dass der beste Fall darin besteht, dass der Quellscheitel derselbe wie der Zielscheitel ist. Das bedeutet, dass sich die Iteration nach nur einer Schleife selbst beendet.
Die Komplexität ist tatsächlich identisch mit dem Durchschnittsfall. Aber da die Werte sowohl von E als auch von V gleich 1 sind, wird dies zu O(1) vereinfacht. Wenn Sie einen Heap verwenden, um Ihren Algorithmus zu implementieren, ändert sich die Komplexität im besten Fall zu O(E* log V). Dies liegt daran, dass Ihre Warteschlange maximal O(E)-Knoten enthält.
Raumkomplexität des Dijkstra-Algorithmus
Wie die zeitliche Komplexität hängt auch die räumliche Komplexität des Algorithmus von Ihrer Implementierung ab. Wenn Sie eine Adjazenzliste verwenden, um Ihren Graphen und einen Fibonacci-Heap oder einen regulären Heap darzustellen, ist die Komplexität gleich O (V + E). Dies liegt daran, dass sowohl der Scheitelabstand von der Quelle als auch die Kanten zwischen den Scheitelpunkten im Speicher gespeichert werden müssen.
Wenn Sie jedoch stattdessen eine Adjazenzmatrix verwenden, wird die Komplexität auf O( V2). Dies liegt daran, dass Sie die Scheitelpunktabstände sowie eine V * V-Matrix speichern müssen, um die Kanten darzustellen.
Zusammenfassung
Zusammenfassend ist der Dijkstra-Algorithmus einer von vielen verwendeten Algorithmen zur Berechnung der kürzesten Weglängen in einem Graphen und ist sehr nützlich. Obwohl es viele Möglichkeiten gibt, den Algorithmus zu implementieren, ist die Verwendung einer Prioritätswarteschlange mit einer bestimmten Beschreibung normalerweise die beste Wahl.
Von diesen Methoden ist die Verwendung eines Fibonacci-Heaps tendenziell die effizienteste, insbesondere für große Graphen. Für kleinere Diagramme kann jedoch eine einfachere Prioritätswarteschlange mehr als ausreichend sein.
Als Nächstes
Dijkstras Shortest-Path-Algorithmus erklärt, mit Beispielen FAQs (häufig gestellte Fragen)
Was ist der Dijkstra-Algorithmus?
Der Algorithmus wird verwendet, um die kürzesten Pfadlängen zwischen Knoten in einem Diagramm zu berechnen. Es handelt sich um eine iterative Methode, die mit der kürzesten Entfernung vom Quellknoten beginnt und dann die Entfernung zu den Nachbarknoten im weiteren Verlauf aktualisiert.
Was sind die Einschränkungen des Dijkstra-Algorithmus?
Der Algorithmus kann keine negativen Gewichtskanten verarbeiten, was zu falschen Ergebnissen führt.
Wie hoch ist die zeitliche Komplexität des Dijkstra-Algorithmus?
Die zeitliche Komplexität hängt davon ab, ob Sie eine Prioritätswarteschlange verwenden und wie Sie diese implementieren. Im besten Fall, wenn nur eine Iteration benötigt wird, ist die Komplexität O(1).
Andernfalls ist der beste Fall entweder O(E* log V) oder O(E + V log V) , abhängig davon, ob Sie einen Standard-Heap oder einen Fibonacci-Heap verwenden.
In beiden Fällen sind die Komplexitäten für den durchschnittlichen und den schlimmsten Fall gleich. Der schlimmste Fall kann O(V2 log V) entsprechen, wenn Sie überhaupt keine Prioritätswarteschlange verwenden.
Was ist die Platzkomplexität von Dijkstras Algorithmus?
Das hängt von der Implementierung ab, kann aber irgendwo zwischen O(V2) und O(V + E) liegen.
Können Sie den Dijkstra-Algorithmus auf einen Graphen mit Zyklen anwenden?
Ja, solange keine der Gewichtskanten negativ ist.
Welche Möglichkeiten gibt es, den Dijkstra-Algorithmus zu implementieren?
Sie können eine Prioritätswarteschlange verwenden, z. B. einen Heap oder einen Fibonacci-Heap. Im Allgemeinen führt ein Fibonacci-Heap zu effizienteren Ergebnissen mit größeren Graphen.
Was sind die Alternativen zum Dijkstra-Algorithmus?
Andere Shortest-Path-Algorithmen umfassen den A * Algorithmus, Bellman-Ford-Algorithmus und Floyd-Warshall-Algorithmus. A* ist tendenziell schneller, erfordert aber mehr Speicher.
Bellman-Ford und Floyd-Warshall können im Gegensatz zu Dijkstra beide mit negativen Gewichtskanten umgehen, aber beide sind ineffizienter als Dijkstra – sie haben Zeitkomplexitäten von O(VE ) bzw. O(V3).