© TippaPatt/Shutterstock.com
นักวิทยาศาสตร์คอมพิวเตอร์มักจะใช้กราฟเพื่อแสดงข้อมูล กราฟสามารถแสดงถึงความสัมพันธ์ต่างๆ ตั้งแต่แผนที่และองค์ประกอบทางเคมีไปจนถึงความสัมพันธ์ทางสังคมและเครือข่ายคอมพิวเตอร์ เราสามารถใช้อัลกอริทึมกับกราฟได้หลายอย่าง เช่น อัลกอริทึมของ Dijkstra, Depth-First Search (DFS) อัลกอริทึมและอัลกอริทึม Breadth-First (หรือ BFS) แม้ว่าคุณสามารถใช้ทั้งสองอัลกอริทึมเพื่อสำรวจโหนดของกราฟได้ แต่ BFS จะดีกว่าสำหรับกราฟที่ไม่ได้ถ่วงน้ำหนัก ในบทความนี้ เราจะมาสำรวจวิธีการทำงานของ BFS และแอปพลิเคชัน
BFS คืออะไร
BFS คืออัลกอริทึมการค้นหา อัลกอริทึมเริ่มต้นการแวะผ่านที่โหนดต้นทางแล้วไปที่โหนดข้างเคียง หลังจากนี้ อัลกอริทึมจะเลือกโหนดที่ใกล้ที่สุดในระดับความลึกถัดไป จากนั้นจึงไปที่โหนดที่ยังไม่ได้สำรวจที่อยู่ถัดจากโหนดนี้ เป็นต้น เนื่องจากอัลกอริทึม BFS เข้าไปที่โหนดในแต่ละระดับก่อนที่จะไปยังระดับถัดไป จึงเป็นที่มาของชื่อ”Breadth-first”เรามั่นใจว่าเราเยี่ยมชมแต่ละโหนดเพียงครั้งเดียวโดยติดตามโหนดที่เยี่ยมชมและไม่ได้เยี่ยมชม คุณสามารถใช้ BFS เพื่อคำนวณระยะทางของเส้นทางได้ เช่นเดียวกับอัลกอริทึมของ Dijkstra
อัลกอริทึมเบื้องหลัง BFS
เราสามารถแสดงอัลกอริทึมพื้นฐานด้วยรหัสเทียมต่อไปนี้:
BFS(graph, start): คิว=[เริ่ม] เยี่ยมชม=ชุด (เริ่มต้น) ในขณะที่คิวไม่ว่างเปล่า: โหนด=dequeue (คิว) กระบวนการ (โหนด) สำหรับเพื่อนบ้านใน enqueue(คิว, เพื่อนบ้าน)
ในกรณีนี้ เรากำหนดกราฟเป็น”กราฟ”และ”เริ่ม”คือโหนดเริ่มต้น
เราใช้โครงสร้างคิวเพื่อเก็บโหนดที่ไม่ได้เข้าชม เช่นเดียวกับชุด”เยี่ยมชม”เพื่อเก็บโหนดที่เยี่ยมชม
การวนซ้ำ”ในขณะที่”จะดำเนินต่อไปจนกว่าคิวจะว่างเปล่า และเริ่มต้นการประมวลผลของโหนดทีละระดับ ฟังก์ชัน”dequeue”จะลบโหนดแรกออกจากคิวขณะที่กำลังเยี่ยมชม
ฟังก์ชัน”กระบวนการ”ทำหน้าที่บางอย่างที่ต้องการบนโหนด เช่น อัปเดตระยะทางไปยังเพื่อนบ้านหรือพิมพ์ข้อมูลไปยัง คอนโซล
ลูป”for”วนซ้ำเพื่อนบ้านทั้งหมดไปยังโหนดปัจจุบัน โดยตรวจสอบว่าโหนดนั้นได้รับการเยี่ยมชมแล้วหรือไม่ หากไม่มี ระบบจะเพิ่มลงในคิวโดยใช้ฟังก์ชัน”enqueue”โดยพื้นฐานแล้ว โหนดในแต่ละระดับจะถูกจัดเก็บไว้ในคิว โดยมีการเพิ่มเพื่อนบ้านเพื่อเข้าชมในระดับความลึกถัดไป ซึ่งช่วยให้เรากำหนดเส้นทางที่สั้นที่สุดระหว่างโหนดต้นทางกับโหนดอื่นๆ ทุกโหนดในกราฟ
การทำงานของ BFS
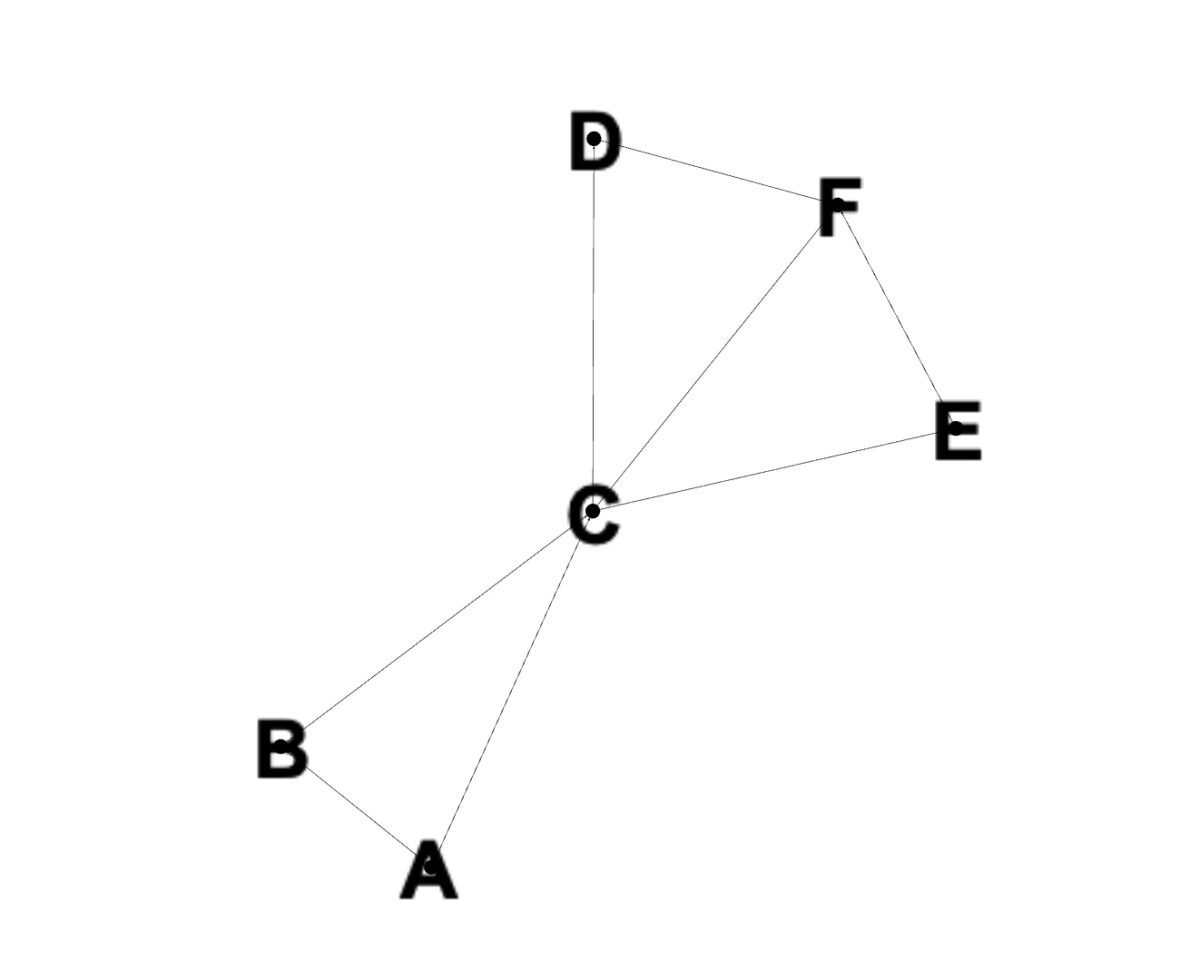เราจะใช้กราฟนี้สำหรับตัวอย่างโค้ดต่อไปนี้
©”TNGD”.com
เมื่ออธิบายพื้นฐานแล้ว ก็ถึงเวลาดูว่า BFS ทำงานอย่างไรในทางปฏิบัติ เราจะอธิบายสิ่งนี้โดยใช้กราฟที่มีโหนด A, B, C, D, E และ F ดังที่แสดงในภาพ โค้ดด้านล่างแสดงวิธีนำ BFS ไปใช้กับกราฟนี้โดยใช้ภาษาการเขียนโปรแกรม Python
from collections import defaultdict, deque def bfs(graph, start): Queue=deque([start]) visit=set([start] ) ในขณะที่คิว: โหนด=queue.popleft() พิมพ์(โหนด) สำหรับเพื่อนบ้านในกราฟ[โหนด]: ถ้าเพื่อนบ้านไม่ได้เข้าชม: เยี่ยมชม.เพิ่ม(เพื่อนบ้าน) คิวผนวก(เพื่อนบ้าน) กราฟ=defaultdict(รายการ) ขอบ=[ (“A”,”B”),”A”,”C”), (“B”,”C”), (“C”,”D”), (“C”,”E”), (“C”,”F”), (“D”,”F”), (“E”,”F”) สำหรับขอบในขอบ: กราฟ[ขอบ[0]].ผนวก(ขอบ[0]) กราฟ[ edge[1]].append(edge[0]) bfs(graph,”A”)
คำอธิบายของโค้ด
ก่อนอื่น เราจะนำเข้าคลาส”defaultdict”และ”deque”จากโมดูล”คอลเลกชัน”สิ่งเหล่านี้ใช้เพื่อสร้างพจนานุกรมที่มีค่าคีย์เริ่มต้น และสร้างคิวที่อนุญาตให้เพิ่มและลบองค์ประกอบ
ต่อไป เรากำลังกำหนดฟังก์ชัน”bfs”ด้วยสองอาร์กิวเมนต์”กราฟ”และ”เริ่ม”. เราใช้อาร์กิวเมนต์”กราฟ”เป็นพจนานุกรมโดยมีจุดยอดเป็นคีย์และจุดใกล้เคียงเป็นค่า ในที่นี้ “start” หมายถึงโหนดต้นทางที่อัลกอริทึมเริ่มต้น
“queue=deque([start])” สร้างคิวที่มีโหนดต้นทางเป็นองค์ประกอบเดียว และ “visited=set ([start])” สร้างชุดของโหนดที่เข้าชมโดยมีโหนดต้นทางเป็นองค์ประกอบเดียว
การวนซ้ำ “ while” จะดำเนินต่อไปจนกว่าคิวจะว่างเปล่า “node=queue.popleft()” ลบองค์ประกอบด้านซ้ายสุดออกจากคิวและเก็บไว้ในตัวแปร “node” “print(node)” พิมพ์ค่าโหนดเหล่านี้
ลูป “for” วนซ้ำเหนือโหนดข้างเคียงแต่ละโหนด “ถ้าเพื่อนบ้านไม่ได้มาเยี่ยม” ตรวจสอบว่าเพื่อนบ้านได้รับการเยี่ยมหรือไม่ “visited.add(neighbor)” เพิ่มเพื่อนบ้านไปยังรายการที่เยี่ยมชม และ “queue.append(neighbor)” เพิ่มเพื่อนบ้านที่ด้านขวาสุดของคิว
หลังจากนี้ เราจะสร้างค่าเริ่มต้น พจนานุกรมเรียกว่า “กราฟ” และกำหนดขอบของกราฟ ลูป”for”วนซ้ำแต่ละขอบ “กราฟ[ขอบ[0]].ผนวก(ขอบ[1])” เพิ่มองค์ประกอบที่สองของขอบเป็นเพื่อนบ้านขององค์ประกอบแรก และองค์ประกอบแรกของขอบเป็นเพื่อนบ้านขององค์ประกอบที่สอง สิ่งนี้สร้างกราฟ
สุดท้าย เราเรียกฟังก์ชัน”bfs”บน”กราฟ”โดยมีโหนดต้นทางเป็น”A”
การนำโค้ดไปใช้
นี่คือลักษณะของอัลกอริทึม BFS เมื่อ นำไปใช้และทำงานผ่านกราฟที่เชื่อมต่อ
©”TNGD”.com
ในภาพหน้าจอ เราจะเห็นผลลัพธ์ [A, B, C, D, E F] นี่คือสิ่งที่เราคาดหวังเนื่องจาก BFS สำรวจโหนดในแต่ละระดับความลึกก่อนที่จะดำเนินการต่อไป อ้างอิงกลับไปที่กราฟ เราจะเห็นว่า B และ C จะถูกเพิ่มในคิวและเข้าชมก่อน B ถูกเยี่ยมชม จากนั้น A และ C จะถูกเพิ่มลงในคิว เนื่องจาก A ถูกเยี่ยมชมแล้ว C ถูกเยี่ยมชมเป็นลำดับถัดไป และ A ถูกลบออก หลังจากนี้เพื่อนบ้านของ C, D, E และ F จะถูกเพิ่มลงในคิว สิ่งเหล่านี้จะถูกเยี่ยมชมและพิมพ์ผลลัพธ์
การใช้ BFS สำหรับกราฟที่ขาดการเชื่อมต่อ
เราใช้ BFS สำหรับกราฟที่เชื่อมต่อก่อนหน้านี้ อย่างไรก็ตาม เรายังสามารถใช้ BFS เมื่อโหนดไม่ได้เชื่อมต่อทั้งหมด เราจะใช้ข้อมูลกราฟเดียวกันเนื่องจากอัลกอริทึมที่แก้ไขสามารถแสดงด้วยกราฟประเภทใดก็ได้ รหัสที่แก้ไขคือ:
จากคอลเลกชัน นำเข้า defaultdict, deque def bfs(กราฟ, เริ่มต้น): คิว=deque ([เริ่ม]) เข้าชม=ชุด ([เริ่ม]) ขณะที่คิว: โหนด=คิว.popleft() พิมพ์ (โหนด) สำหรับเพื่อนบ้านในกราฟ [โหนด]: หากเพื่อนบ้านไม่ได้เข้าชม: เยี่ยมชม.เพิ่ม (เพื่อนบ้าน) คิวต่อท้าย (เพื่อนบ้าน) สำหรับโหนดในกราฟ คีย์ (): หากโหนดไม่ได้เข้าชม: คิว=deque ([โหนด ]) เยี่ยมชม.เพิ่ม(โหนด) ในขณะที่คิว: โหนด=คิว.popleft() พิมพ์(โหนด) สำหรับเพื่อนบ้านในกราฟ[โหนด]: ถ้าเพื่อนบ้านไม่ได้อยู่ในการเยี่ยมชม: เยี่ยมชม.เพิ่ม(เพื่อนบ้าน) คิวผนวก(เพื่อนบ้าน) กราฟ=defaultdict(รายการ) ขอบ=[(“A”,”B”), (“A”,”C”), (“B”,”C”), (“C”,”D”), (“C”,”E”), (“C”,”F”), (“D”,”F”), (“E”,”F”)] สำหรับขอบในขอบ: กราฟ[ขอบ[0]] ผนวก(ขอบ[1]) กราฟ[ขอบ[1]].ผนวก(ขอบ[0]) bfs(กราฟ,”A”)
เราใช้ลูป”for”เพิ่มเติม การวนซ้ำจะวนซ้ำทุกโหนดโดยใช้เมธอด “graph.keys()” BFS จะเริ่มคิวใหม่หากพบโหนดที่ไม่ได้เยี่ยมชมและทำงานซ้ำ เมื่อทำเช่นนี้ เราจะไปที่โหนดที่ไม่ได้เชื่อมต่อทั้งหมด ดูภาพประกอบด้านล่าง
นี่คือตัวอย่างของอัลกอริทึม BFS เมื่อใช้งานและทำงานผ่านกราฟที่ไม่ได้เชื่อมต่อ
©”TNGD”.com
กรณีการใช้งานที่ดีที่สุดและแย่ที่สุดสำหรับ BFS
ตอนนี้เรารู้แล้วว่า BFS ทำงานอย่างไร เราควรดูเวลาและพื้นที่ที่ซับซ้อนของอัลกอริทึมเพื่อทำความเข้าใจกรณีการใช้งานที่ดีที่สุดและแย่ที่สุด
ความซับซ้อนของเวลาของ BFS
เราจะเห็นว่าความซับซ้อนของเวลาเท่ากันในทุกกรณี และเท่ากับ O(V + E) โดยที่ V คือจำนวนจุดยอด และ E คือจำนวนขอบ ในกรณีที่ดีที่สุดที่เรามีเพียงโหนดเดียว ความซับซ้อนจะเป็น O(1) เนื่องจาก V=1 และ E=0 ในกรณีเฉลี่ยและแย่ที่สุด อัลกอริทึมจะเข้าเยี่ยมชมโหนดทั้งหมดที่สามารถเข้าถึงได้จากโหนดต้นทาง ดังนั้นความซับซ้อนจึงขึ้นอยู่กับโครงสร้างและขนาดของกราฟในทั้งสองกรณี
Space Complexity of BFS
อีกครั้ง เราพบว่าความซับซ้อนนั้นเหมือนกันในทุกกรณี อัลกอริทึมเยี่ยมชมแต่ละโหนดไม่ว่าโครงสร้างกราฟจะเป็นอย่างไร ดังนั้น ความซับซ้อนจึงขึ้นอยู่กับจำนวนจุดยอดในกราฟ
การสรุปผล
BFS เป็นวิธีหนึ่งในการสำรวจโหนดในกราฟ คำนวณระยะทางของเส้นทาง และสำรวจความสัมพันธ์ระหว่าง โหนด เป็นอัลกอริธึมที่มีประโยชน์มากสำหรับการสำรวจระบบเครือข่ายและตรวจจับวงจรของกราฟ BFS ใช้งานได้ค่อนข้างง่ายสำหรับทั้งกราฟที่เชื่อมต่อและไม่ได้เชื่อมต่อ ข้อดีคือความซับซ้อนของเวลาและพื้นที่จะเท่ากันในทุกกรณี
Breadth-First Search (BFS) สำหรับกราฟ – อธิบายพร้อมตัวอย่าง คำถามที่พบบ่อย (คำถามที่พบบ่อย)
BFS คืออะไร
BFS เป็นอัลกอริทึมที่ใช้สำหรับสำรวจต้นไม้หรือกราฟ ซึ่งโดยปกติจะเป็นเครือข่ายที่เป็นตัวแทนของเครือข่าย เช่น เครือข่ายโซเชียลหรือเครือข่ายคอมพิวเตอร์ นอกจากนี้ยังสามารถตรวจจับรอบของกราฟหรือหากกราฟเป็นสองส่วน ตลอดจนคำนวณระยะทางของเส้นทางที่สั้นที่สุด ความกว้างมาก่อนหมายความว่าแต่ละโหนดได้รับการสำรวจในระดับความลึกเฉพาะก่อนที่จะดำเนินการต่อไป
เวลาที่ซับซ้อนของ BFS คืออะไร
ความซับซ้อนของเวลาของ BFS คือ O(V + E) ในทุกกรณี
ความซับซ้อนของพื้นที่ของ BFS คืออะไร
ความซับซ้อนของพื้นที่ของ BFS คือ O(V) ในทุกกรณี
เมื่อใดที่คุณควรใช้ BFS
หากคุณต้องการคำนวณระยะทางของเส้นทางที่สั้นที่สุด หรือสำรวจจุดยอดทั้งหมดใน กราฟที่ไม่มีการถ่วงน้ำหนัก
BFS นำไปใช้อย่างไร
โดยปกติเราจะนำ BFS ไปใช้โดยใช้โครงสร้างข้อมูลคิวและชุดเพื่อติดตามโหนดที่เยี่ยมชมและไม่ได้เยี่ยมชม. โหนดต้นทางถูกเพิ่มลงในคิวและทำเครื่องหมายว่าเข้าชมแล้ว จากนั้น อัลกอริทึมจะทำงานซ้ำกับโหนดข้างเคียง เพิ่มและลบโหนดเมื่อดำเนินไป เพื่อให้แน่ใจว่าไม่มีโหนดถูกเยี่ยมชมซ้ำสอง
BFS เปรียบเทียบกับอัลกอริทึมของ Dijkstra อย่างไร
อัลกอริทึมเหล่านี้สามารถใช้ในการคำนวณระยะทางของเส้นทางที่สั้นที่สุด แต่ BFS ทำงานร่วมกับกราฟที่ไม่ได้ถ่วงน้ำหนัก ในทางตรงกันข้าม อัลกอริทึมของ Dijkstra ทำงานร่วมกับกราฟที่มีการถ่วงน้ำหนัก
DFS เปรียบเทียบกับ BFS อย่างไร
ทั้งสองอย่างนี้ใช้เพื่อสำรวจกราฟ แต่ต่างกันตรงที่ พวกเขาทำสิ่งนี้อย่างไร ในขณะที่ BFS ค้นหาแต่ละโหนดที่ระดับความลึกที่กำหนดก่อนที่จะดำเนินการต่อ DFS จะเข้าไปที่โหนดในระดับความลึกมากที่สุดเท่าที่จะเป็นไปได้ก่อนที่จะกลับเข้าไปสำรวจสาขาอื่น โดยปกติแล้ว DFS จะใช้โครงสร้างข้อมูลแบบสแตกแทนที่จะเป็นคิว