อธิบายอัลกอริทึมการเรียงลำดับการเลือกพร้อมตัวอย่าง

มีอัลกอริทึมการเรียงลำดับมากมายที่สามารถใช้เพื่อจัดเรียงชุดข้อมูล โดยทั่วไปแล้ว ข้อมูลนี้จะแสดงเป็นรายการหรืออาร์เรย์ ในอัลกอริทึมเหล่านี้ อัลกอริทึมการเรียงลำดับการเลือกเป็นหนึ่งในวิธีที่ง่ายที่สุดในการทำความเข้าใจและนำไปใช้ ในบทความนี้ เราจะอธิบายทฤษฎีเบื้องหลังการเรียงลำดับการเลือก วิธีการนำไปใช้ และแนวทางปฏิบัติที่ดีที่สุดสำหรับการใช้อัลกอริทึม

การเรียงลำดับการเลือกคืออะไร

การเรียงลำดับการเลือกคือ อัลกอริทึมการเรียงลำดับตามการเปรียบเทียบ มันทำงานโดยแบ่งอาร์เรย์ออกเป็นสองส่วน – เรียงลำดับและไม่เรียงลำดับ องค์ประกอบที่มีค่าน้อยที่สุดจะถูกเลือก และวางไว้ที่ดัชนี 0 ของแถบย่อยที่เรียงลำดับ นอกจากนี้ยังสามารถเลือกองค์ประกอบที่ใหญ่ที่สุดก่อน ขึ้นอยู่กับว่าคุณต้องการให้รายการของคุณอยู่ในลำดับจากน้อยไปหามากหรือจากมากไปน้อย นี่เป็นกระบวนการวนซ้ำ ซึ่งหมายถึงวิธีการทำซ้ำจนกว่าองค์ประกอบทั้งหมดจะถูกวางลงในอาร์เรย์ที่เรียงลำดับในตำแหน่งที่ถูกต้อง อย่างที่คุณคาดไว้ ด้วยการวนซ้ำแต่ละครั้ง ขนาด subarray ที่เรียงลำดับจะเพิ่มขึ้น 1 องค์ประกอบ ในขณะที่ขนาดอาร์เรย์ที่ไม่เรียงลำดับจะลดลง 1 องค์ประกอบ

คุณสามารถใช้การเรียงลำดับการเลือกกับภาษาการเขียนโปรแกรมที่หลากหลาย รวมถึง C, C++, C#, PHP, Java, Javascript และ หลาม

อัลกอริทึมเบื้องหลังการจัดเรียงการเลือก

อัลกอริทึมเบื้องหลังการจัดเรียงการเลือกนั้นค่อนข้างเรียบง่าย และทำตามขั้นตอนเหล่านี้:

พบองค์ประกอบขั้นต่ำในอาร์เรย์ที่ไม่เรียงลำดับและสลับกับองค์ประกอบแรกในดัชนี 0 จากนั้นอาร์เรย์ที่ไม่เรียงลำดับจะ ข้ามไปหาองค์ประกอบขั้นต่ำใหม่ หากพบว่าองค์ประกอบใดมีขนาดเล็กกว่าองค์ประกอบในดัชนี 0 องค์ประกอบนั้นจะถูกสับเปลี่ยน พบองค์ประกอบขั้นต่ำถัดไปในอาร์เรย์ที่ไม่เรียงลำดับ และเพิ่มไปยัง subarray ที่เรียงลำดับ ตามข้อจำกัดก่อนหน้า กระบวนการนี้จะเกิดขึ้นซ้ำๆ จนกว่าจะจัดเรียงอาร์เรย์ทั้งหมด

การทำงานของ Selection Sort

ตอนนี้เราได้อธิบายถึงวิธีการทำงานของ Selection Sort แล้ว ถึงเวลาอธิบายด้วยตัวอย่าง

หากเราพิจารณา array [72, 61, 59, 47, 21]:

การผ่านครั้งแรกหรือการวนซ้ำของกระบวนการเกี่ยวข้องกับการสำรวจอาร์เรย์ทั้งหมดจากดัชนี 0 ถึงดัชนี 4 (จำไว้ว่าดัชนีแรกถูกกำหนดเป็น 0 ไม่ใช่ 1)

องค์ประกอบขั้นต่ำที่พบคือ 21 ดังนั้นจึงสลับกับองค์ประกอบแรก 72 นี่คือภาพประกอบด้านล่าง

[21, 61, 59, 47, 72]

โดยที่สีเขียว=องค์ประกอบที่เรียงลำดับ

สำหรับรอบที่สอง เราพบว่า 47 เป็นค่าที่น้อยที่สุดเป็นอันดับสอง จากนั้นจะสลับด้วย 61

[21, 47, 59, 61, 72]

รอบที่สามตรวจพบ 59 เป็นองค์ประกอบที่สามซึ่งอยู่ในตำแหน่งแล้ว ดังนั้นจึงไม่มีการสลับเกิดขึ้น

[21, 47, 59, 61, 72]

การส่งครั้งที่สี่พบว่า 61 เป็นองค์ประกอบที่สี่ซึ่งอีกครั้งอยู่ในตำแหน่งแล้ว

[21, 47, 59, 61, 72]

ผลการจ่ายบอลครั้งที่ห้าและรอบสุดท้ายเหมือนกันมาก 72 เป็นองค์ประกอบที่เล็กที่สุดอันดับที่ห้าหรือใหญ่ที่สุด และอยู่ในตำแหน่งที่ถูกต้อง ตอนนี้ อาร์เรย์ถูกจัดเรียงจากน้อยไปมาก

[21, 47, 59, 61, 72]

การดำเนินการ Selection Sort

เราสามารถใช้ จัดเรียงการเลือกด้วยภาษาการเขียนโปรแกรมที่หลากหลาย รวมถึงภาษาที่ใช้บ่อยที่สุด – C, C++, C#, PHP, Java, Javascript และ Python เพื่อเป็นตัวอย่าง เราจะใช้ Python โค้ดที่ใช้กับ Python มีดังนี้

def SSort(arr, size): for step in range(size): min_idx=step for i in range(step + 1, size): if arr[i] arr [min_idx]: min_idx=i (arr[ขั้นตอน], arr[min_idx])=(arr[min_idx], arr[ขั้นตอน]) data=[-7, 39, 0, 14, 7] size=len(ข้อมูล) SSort(data, size) print(‘Ascending Sorted Array:’) print(data)

คำอธิบายโค้ด

ในขั้นตอนนี้ คำอธิบายโค้ดที่ใช้จะเป็นประโยชน์ ประการแรก เรากำหนดฟังก์ชัน “SSort” เป็นฟังก์ชันของอาร์เรย์ที่มีขนาดที่ระบุ

ลูป “for” กำหนดให้ลูปเริ่มต้นซึ่งจะวนซ้ำในช่วง “ขนาด” ซึ่งหมายถึง ความยาวของอาร์เรย์ ตัวแปร “step” ระบุว่าการวนซ้ำแต่ละครั้งจะใช้ค่า 0, 1, 2… จนถึงขนาด-1

บรรทัดถัดไปแสดงว่าค่าเริ่มต้นของ “step” เท่ากับตัวแปร “ min_idx” นี่เป็นวิธีการติดตามตำแหน่งขององค์ประกอบขั้นต่ำในอาร์เรย์ที่ไม่เรียงลำดับ

ลูป”for”ถัดไประบุลูปที่จะวนซ้ำเหนืออาร์เรย์ที่ไม่เรียงลำดับ โดยเริ่มต้นที่”ขั้นตอน + 1″. นี่เป็นเพราะองค์ประกอบ”ขั้นตอน”ถูกวางไว้ในอาร์เรย์ที่เรียงลำดับแล้ว ตัวแปร “i” ในการวนซ้ำแต่ละครั้งจะเทียบเท่ากับ step + 1, step + 2 และอื่นๆ จนถึงขนาด – 1

คำสั่ง “if” ที่ตรวจสอบว่าองค์ประกอบปัจจุบันที่ “i” น้อยกว่าองค์ประกอบขั้นต่ำปัจจุบัน หากพบว่าเป็นกรณีนี้ องค์ประกอบขั้นต่ำจะได้รับการอัปเดตเพื่อแสดงสิ่งนี้

สุดท้าย บรรทัดที่ค่อนข้างซับซ้อนนี้มีความหมายง่ายๆ เมื่อลูปก่อนหน้าเสร็จสิ้น องค์ประกอบที่ไม่เรียงลำดับขั้นต่ำจะถูกสลับกับองค์ประกอบแรกในอาร์เรย์ที่ไม่เรียงลำดับ วิธีนี้จะเพิ่มองค์ประกอบที่ส่วนท้ายของอาร์เรย์ที่เรียงลำดับได้อย่างมีประสิทธิภาพ

โค้ดด้านล่างจะกำหนดอาร์เรย์ที่เรากำลังดำเนินการด้วยความยาว”ขนาด”และเรียกการเรียงลำดับการเลือกเพื่อทำงานนี้ อาร์เรย์ ผลลัพธ์จะถูกพิมพ์ด้วยชื่อ”Ascending Sorted Array”

เมื่อใดก็ตามที่ใช้ Python จำเป็นอย่างยิ่งที่คุณต้องใช้การเยื้องที่ถูกต้องเพื่อกำหนดการดำเนินการที่แยกจากกัน มิฉะนั้น คุณจะได้รับข้อความแสดงข้อผิดพลาดและการคำนวณจะไม่ทำงาน

โค้ดมีลักษณะอย่างไร

ดูภาพหน้าจอด้านล่างเพื่อดูว่าโค้ดนี้มีลักษณะอย่างไรเมื่อใช้งานใน Python

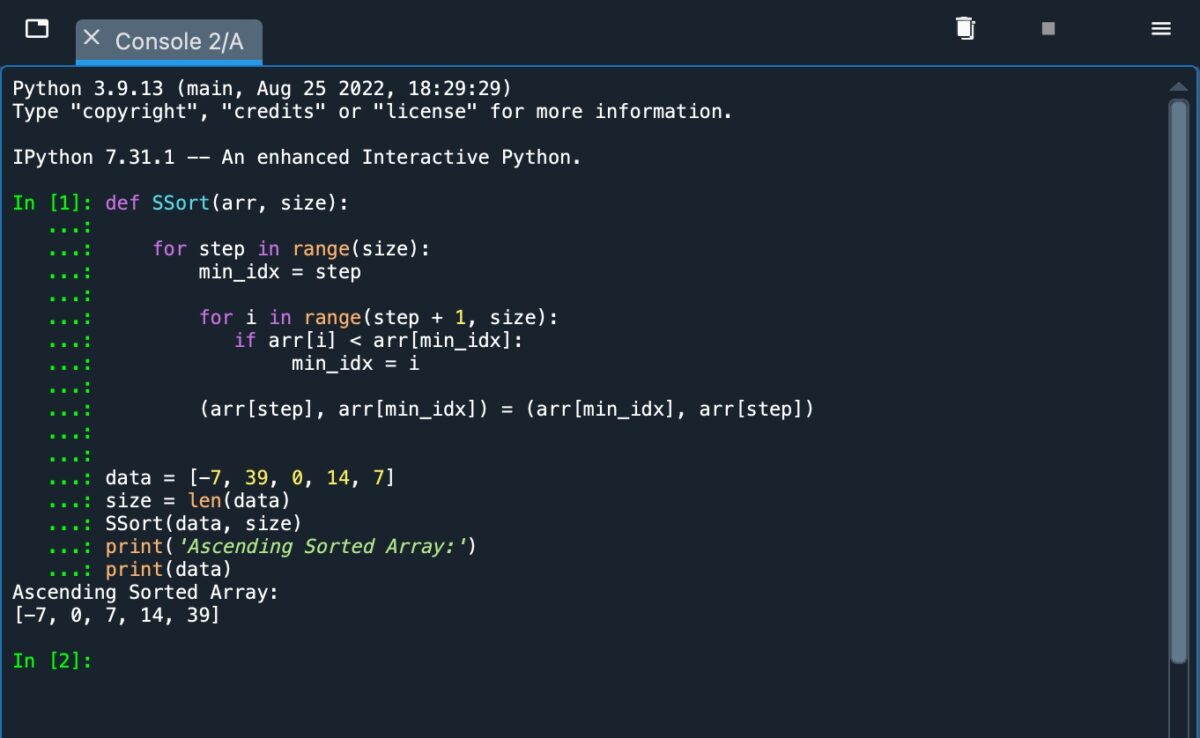เมื่อใช้ Python คุณต้องใช้การเยื้องที่ถูกต้องเพื่อกำหนดการดำเนินการแยกกัน

©”TNGD”.com

กรณีการใช้งานการเรียงลำดับการแทรกที่ดีที่สุดและแย่ที่สุด

การเรียงลำดับการแทรกมีประโยชน์ สำหรับวัตถุประสงค์หลายๆ อย่าง เช่นเดียวกับอัลกอริทึมใดๆ ก็มีทั้งกรณีที่ดีที่สุดและแย่ที่สุด โดยมากจะขึ้นอยู่กับความซับซ้อนของเวลาและพื้นที่

ความซับซ้อนของเวลาที่มีการเรียงลำดับการแทรก

ความซับซ้อนของเวลาในแต่ละกรณีสามารถอธิบายได้ในตารางต่อไปนี้:

เช่น ด้วยอัลกอริทึมใด ๆ การเรียงลำดับการเลือกจะมีความซับซ้อนของเวลาและพื้นที่ของตัวเอง โดยพื้นฐานแล้วหมายถึงความซับซ้อนหรือความเร็วของการดำเนินการที่เปลี่ยนแปลงไปในหลายกรณี สามารถสรุปความซับซ้อนของเวลาได้ในตารางต่อไปนี้:

กรณีที่ดีที่สุดหมายถึงเมื่อมีการจัดเรียงอาร์เรย์ กรณีเฉลี่ยหมายถึงเมื่ออาร์เรย์สับสน และกรณีที่แย่ที่สุดหมายถึงเมื่ออาร์เรย์อยู่ในลำดับจากน้อยไปหามากหรือจากมากไปหาน้อย และคุณต้องการลำดับที่ตรงกันข้าม กล่าวอีกนัยหนึ่งคือหมายถึงจำนวนการวนซ้ำที่จำเป็นเพื่อให้กระบวนการเสร็จสมบูรณ์ โดยกรณีที่เลวร้ายที่สุดต้องการจำนวนการวนซ้ำสูงสุด

สำหรับกรณีนี้ ความซับซ้อนของเวลาจะเหมือนกันสำหรับการเรียงลำดับการเลือกในทุกๆ กรณี. นี่เป็นเพราะอัลกอริทึมทำการเปรียบเทียบและสลับจำนวนเท่ากันเสมอ ไม่ว่าอาร์เรย์จะเรียงลำดับอย่างไร ดังนั้นความซับซ้อนคือ O(n2) หรือที่เรียกว่าเวลากำลังสอง นี่เป็นเหตุผลหลักว่าทำไมอัลกอริทึมถึงไม่มีประสิทธิภาพเท่าอัลกอริทึมการเรียงลำดับ แต่ก็หมายความว่าประสิทธิภาพไม่ได้ขึ้นอยู่กับการกระจายของอินพุต

ความซับซ้อนของพื้นที่ด้วยการจัดเรียงการเลือก

ความซับซ้อนของพื้นที่หมายถึงจำนวนหน่วยความจำที่จำเป็นสำหรับการคำนวณ ในกรณีของการเรียงลำดับการเลือก ค่านี้จะเท่ากับ O(1) ซึ่งหมายความว่าจำเป็นต้องใช้หน่วยความจำในจำนวนคงที่ โดยไม่ขึ้นกับขนาดอินพุต ตัวแปรชั่วคราวตัวเดียวที่เก็บไว้คือ “min_idx” ซึ่งไม่เปลี่ยนแปลงตามขนาดอินพุตที่เพิ่มขึ้น

สรุป

การเรียงลำดับการเลือกเป็นอัลกอริทึมที่ค่อนข้างง่ายแต่ไม่มีประสิทธิภาพสำหรับการเรียงลำดับองค์ประกอบ ในอินพุตที่กำหนด ส่วนใหญ่เหมาะสำหรับชุดข้อมูลขนาดเล็กมาก และสามารถนำไปใช้กับภาษาโปรแกรมต่างๆ ได้ การเรียงลำดับการเลือกทำงานโดยการแบ่งอาร์เรย์ออกเป็นสองอาร์เรย์ย่อย ทั้งแบบเรียงลำดับและไม่เรียงลำดับ จากนั้นกระบวนการจะเคลื่อนผ่านอาร์เรย์เพื่อค้นหาองค์ประกอบขั้นต่ำ และย้ายองค์ประกอบนี้ไปที่ดัชนี 0 กระบวนการนี้จะเกิดขึ้นซ้ำๆ โดยค้นหาองค์ประกอบที่เล็กที่สุดอันดับสองและสามและต่อไปเรื่อยๆ และสลับไปยังตำแหน่งดัชนีที่ถูกต้อง สิ่งนี้จะดำเนินต่อไปจนกว่าจะจัดเรียงอาร์เรย์ทั้งหมด

ถัดไป…

อธิบายอัลกอริทึมการจัดเรียงการเลือกพร้อมตัวอย่าง คำถามที่พบบ่อย (คำถามที่พบบ่อย) 

อะไร เป็นการเรียงลำดับการเลือกหรือไม่

การเรียงลำดับการเลือกเป็นอัลกอริทึมการเรียงลำดับอย่างง่ายที่เรียงลำดับอาร์เรย์ขององค์ประกอบตามลำดับจากน้อยไปมากหรือจากมากไปน้อย ทำสิ่งนี้โดยสำรวจอาร์เรย์เพื่อค้นหาองค์ประกอบขั้นต่ำ และสลับสิ่งนี้กับองค์ประกอบในดัชนี 0 ในแถบย่อยที่เรียงลำดับ จากนั้น subarray ที่ไม่เรียงลำดับจะถูกสำรวจอีกครั้ง และพบองค์ประกอบขั้นต่ำและสลับไปยังตำแหน่งที่ถูกต้อง อัลกอริทึมจะทำซ้ำขั้นตอนนี้จนกว่าอาร์เรย์ทั้งหมดจะถูกจัดเรียง การเรียงลำดับแบบเลือกเป็นอัลกอริทึมการเรียงลำดับอย่างง่ายที่ทำงานโดยการค้นหาองค์ประกอบขั้นต่ำซ้ำๆ จากส่วนที่ไม่ได้เรียงลำดับของอาร์เรย์ และวางไว้ที่จุดเริ่มต้นของส่วนที่เรียงลำดับของอาร์เรย์ อัลกอริทึมรักษาสอง subarrays ในอาร์เรย์ที่กำหนด

ข้อดีของการเรียงลำดับการเลือกคืออะไร

การเรียงลำดับการเลือกเป็นอัลกอริทึมที่ง่ายมากในการทำความเข้าใจและนำไปใช้ และเพียงพอสำหรับชุดข้อมูลขนาดเล็กมาก

ข้อเสียของการเรียงลำดับแบบเลือกคืออะไร

เนื่องจากไม่มีประสิทธิภาพมาก การเรียงลำดับแบบเลือกจึงไม่เพียงพอใน จัดการกับชุดข้อมูลขนาดใหญ่ ประสิทธิภาพของมันไม่ได้ขึ้นอยู่กับการกระจายอินพุต แต่ก็หมายความว่ามันไม่มีประสิทธิภาพในทุกกรณี ไม่ว่าอาร์เรย์เริ่มต้นจะเรียงลำดับอย่างไรก็ตาม นอกจากนี้ยังไม่ใช่อัลกอริทึมที่เสถียร หมายความว่าลำดับสัมพัทธ์ขององค์ประกอบที่เท่ากันอาจไม่ถูกรักษาไว้ สรุปแล้ว มีอัลกอริทึมการเรียงลำดับที่เหนือกว่าสำหรับกรณีส่วนใหญ่ ซึ่งสามารถปรับให้เข้ากับอินพุตที่เป็นปัญหาได้ดีกว่า

สถานการณ์ใดดีที่สุดสำหรับการใช้การเรียงลำดับแบบเลือก

การเรียงลำดับการเลือกจะใช้ได้ดีที่สุดเมื่อขนาดอินพุตมีขนาดเล็ก และคุณต้องการโซลูชันที่เรียบง่ายและมีประสิทธิภาพ เนื่องจากความซับซ้อนของพื้นที่คือ O(1) การเรียงลำดับการเลือกจึงมีข้อดีหากการใช้หน่วยความจำเป็นสิ่งที่คุณต้องดู เนื่องจากดำเนินการวนซ้ำในจำนวนที่เท่ากันเสมอ จึงอาจทำงานได้ดีกว่าอัลกอริทึมอื่นๆ เมื่อจัดเรียงอาร์เรย์ที่จัดเรียงแล้วบางส่วน เนื่องจากการใช้เวลาเท่าเดิมย่อมดีกว่าการใช้เวลานาน หากคุณไม่ต้องการอัลกอริทึมการเรียงลำดับที่เสถียร การเรียงลำดับการเลือกเป็นทางเลือกที่ทำงานได้

ความซับซ้อนของเวลาของการเรียงลำดับการเลือกคืออะไร

เวลา ความซับซ้อนของการเรียงลำดับการเลือกเป็นแบบกำลังสอง ซึ่งแสดงเป็น O(n2)

ความซับซ้อนของช่องว่างของการเรียงลำดับการเลือกคืออะไร

ความซับซ้อนของช่องว่างคือ O( 1). ซึ่งหมายความว่าจะใช้หน่วยความจำจำนวนคงที่สำหรับการวนซ้ำแต่ละครั้ง เนื่องจากจำเป็นต้องเก็บตัวแปรชั่วคราวเพียงตัวเดียว แม้ว่าอัลกอริทึมอาจไม่มีประสิทธิภาพ แต่ความซับซ้อนของพื้นที่หมายความว่าอัลกอริทึมมีข้อได้เปรียบในสถานการณ์ที่จำกัดการใช้หน่วยความจำ

ทางเลือกในการจัดเรียงการเลือกมีอะไรบ้าง

อัลกอริทึมการเรียงลำดับอื่นๆ จำนวนมากจะมีประสิทธิภาพมากกว่าในกรณีการใช้งานส่วนใหญ่ ซึ่งรวมถึงการเรียงลำดับแบบผสาน การเรียงลำดับแบบรวดเร็ว และการเรียงลำดับแบบฮีป อัลกอริทึมเหล่านี้มีแนวโน้มที่จะปรับเปลี่ยนได้มากกว่า และมีความซับซ้อนของเวลาที่ดีกว่ามาก ในบรรดาทางเลือกเหล่านี้ การจัดเรียงแบบผสานเป็นอัลกอริทึมเดียวที่เสถียร ดังนั้นจึงเป็นไปได้ในกรณีที่คุณต้องรักษาลำดับสัมพัทธ์ขององค์ประกอบที่เท่ากัน

การเรียงลำดับการเลือกเป็นอัลกอริทึมที่เสถียรหรือไม่

ไม่ มันไม่ใช่อัลกอริทึมที่เสถียร ซึ่งหมายความว่า เมื่อจัดเรียงอาร์เรย์ องค์ประกอบที่มีค่าเท่ากันอาจไม่ถูกรักษาไว้ในลำดับเดิมหลังจากการสลับเกิดขึ้น