© whiteMocca/Shutterstock.com
อัลกอริทึมการเรียงลำดับมักจะแบ่งออกเป็นสองกลุ่ม — ง่ายต่อการติดตั้งหรือเรียกใช้เร็วกว่า การจัดเรียงอย่างรวดเร็วส่วนใหญ่จะอยู่ในประเภทหลัง อ่านเพื่อหาวิธีใช้อัลกอริทึมนี้และสถานการณ์ที่ดีที่สุดที่จะใช้สำหรับ
Quick Sort คืออะไร
Quick sort คืออัลกอริทึมการเรียงลำดับที่ใช้สำหรับการจัดระเบียบอาร์เรย์ของ ข้อมูล. โดยพื้นฐานแล้วอาศัยหลักการที่เรียกว่าการแบ่งแยกและพิชิต นี่คือวิธีการที่เราแบ่งปัญหาที่ใหญ่กว่าและซับซ้อนกว่าออกเป็นปัญหาย่อยที่ง่ายกว่า จากนั้นปัญหาย่อยเหล่านี้จะได้รับการแก้ไขและวิธีแก้ไขจะรวมกันเพื่อค้นหาวิธีแก้ไขปัญหาดั้งเดิม

อัลกอริทึมเบื้องหลัง Quick Sort
นี่ไม่ใช่วิธีการใช้การเรียงลำดับอย่างรวดเร็ว แต่ให้แนวคิดว่า ใช้งานได้
//i-> ดัชนีเริ่มต้น, j–> สิ้นสุดดัชนี Quicksort(array, i, j) { if (i j) { pIndex=Partition(A, i, j) Quicksor(A,i, pIndex-1) Quicksort(A,pIndex+1, end) } }
ก่อนอื่น เรากำหนดให้การเรียงลำดับอย่างรวดเร็วเป็นฟังก์ชันของอาร์เรย์ที่มีองค์ประกอบเริ่มต้นและองค์ประกอบสิ้นสุด คำสั่ง”if”จะตรวจสอบว่าอาร์เรย์มีองค์ประกอบมากกว่าหนึ่งรายการ
ในกรณีนี้ เราเรียกฟังก์ชัน”พาร์ติชัน”ซึ่งให้ดัชนีขององค์ประกอบ”pivot”สิ่งนี้จะแยกอาร์เรย์ออกเป็นสองอาร์เรย์ย่อย โดยมีองค์ประกอบที่เล็กกว่าและมากกว่าเดือยตามลำดับ
ฟังก์ชันนี้ถูกเรียกซ้ำในแต่ละ subarray จนกว่าแต่ละ subarray จะมีเพียงองค์ประกอบเดียว จากนั้นอาร์เรย์ที่จัดเรียงจะถูกส่งคืนและกระบวนการเสร็จสิ้น
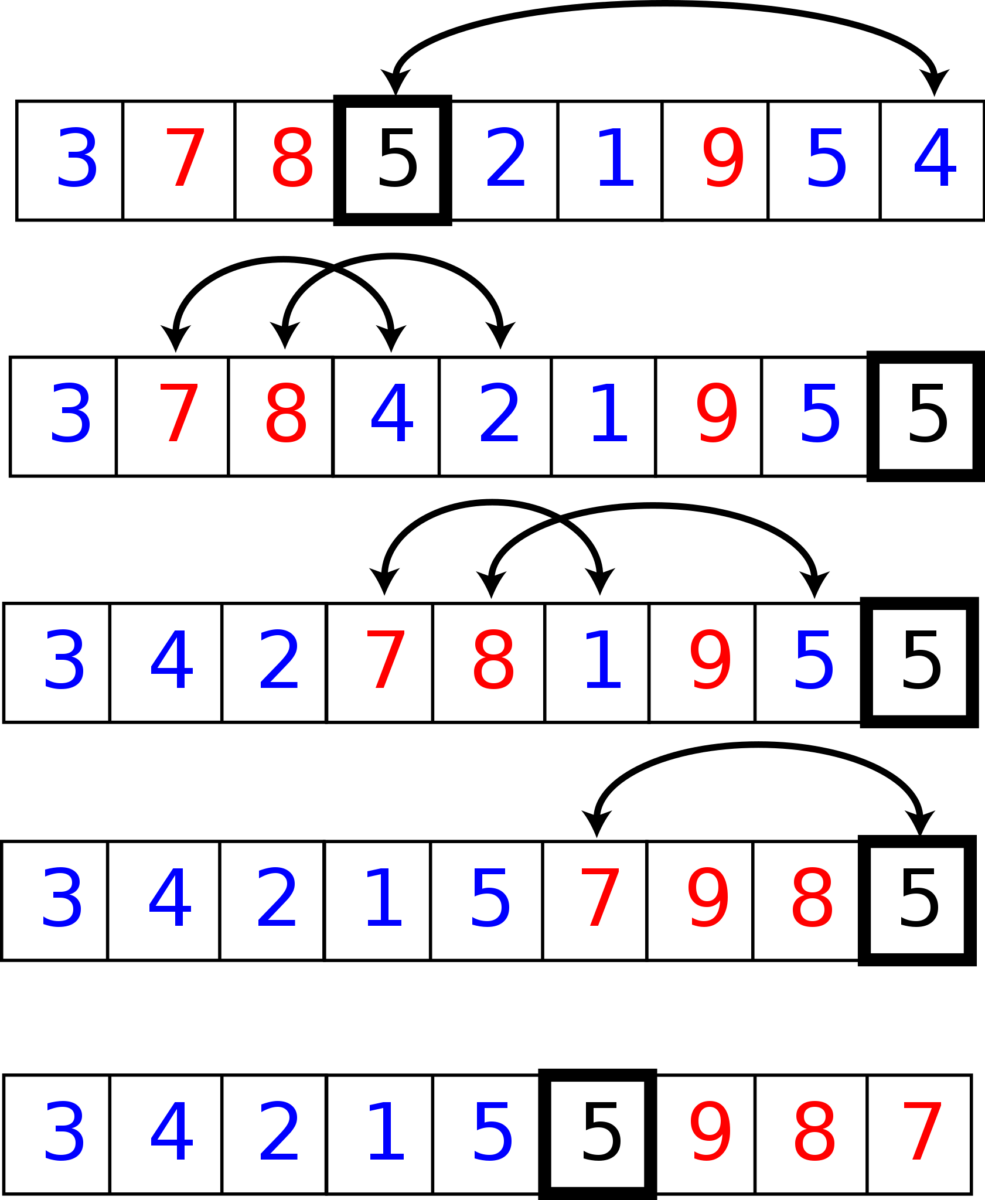 ในตัวอย่างนี้ องค์ประกอบที่เป็นกล่องคือองค์ประกอบเดือย องค์ประกอบสีน้ำเงินมีค่าเท่ากับหรือเล็กกว่า และองค์ประกอบสีแดงมีค่ามากกว่า
ในตัวอย่างนี้ องค์ประกอบที่เป็นกล่องคือองค์ประกอบเดือย องค์ประกอบสีน้ำเงินมีค่าเท่ากับหรือเล็กกว่า และองค์ประกอบสีแดงมีค่ามากกว่า
©Dcoetzee/Public Domain – ใบอนุญาต
ตัวอย่าง Quick Sort
อย่างรวดเร็ว การเรียงลำดับจะอธิบายได้ดีที่สุดโดยใช้ตัวอย่างเพื่ออธิบาย
ลองใช้อาร์เรย์ต่อไปนี้ – [56, 47, 98, 3, 6, 7, 11]
เรามี ดัชนีตั้งแต่ 0 ถึง 6 (จำไว้ว่าองค์ประกอบแรกคือดัชนี 0 ไม่ใช่ 1)
การใช้องค์ประกอบสุดท้ายเป็นเดือย อาร์เรย์จะถูกจัดเรียงใหม่เพื่อให้องค์ประกอบที่เล็กกว่าเดือยอยู่ทางซ้าย และ องค์ประกอบขนาดใหญ่อยู่ทางด้านขวา สิ่งนี้ทำได้โดยการเริ่มต้นตัวแปร i และ j เป็น 0 ถ้า arr[j] หรือองค์ประกอบปัจจุบัน มีขนาดเล็กกว่า pivot เราจะสลับด้วย arr[i] และทำเช่นนี้ทีละน้อย จากนั้นเปลี่ยนเดือยด้วย arr[i] เพื่อให้องค์ประกอบนี้อยู่ในตำแหน่งที่เรียงลำดับ
ซึ่งจะทำให้มีแถบย่อย [6, 7, 3] และ [56, 47, 98] ดัชนีขององค์ประกอบ Pivot ในขณะนี้คือ 3 แทนที่จะเป็น 6
จากนั้นเรียกการจัดเรียงแบบด่วน ซึ่งจะจัดเรียงแถบย่อยด้านซ้ายรอบๆ องค์ประกอบ Pivot 3 โดยการจัดเรียงแถบย่อย [6] และ [7]
จากนั้นเราเรียกการเรียงลำดับอย่างรวดเร็วซ้ำบนแถบย่อยด้านขวา เพื่อให้จัดเรียงเป็น [47, 56, 98]
ในที่สุด แถบย่อยจะถูกรวมเข้าด้วยกันเพื่อให้เป็นอาร์เรย์ที่เรียงลำดับ – [3, 6, 7, 11, 47, 56, 98].
การนำไปใช้งาน
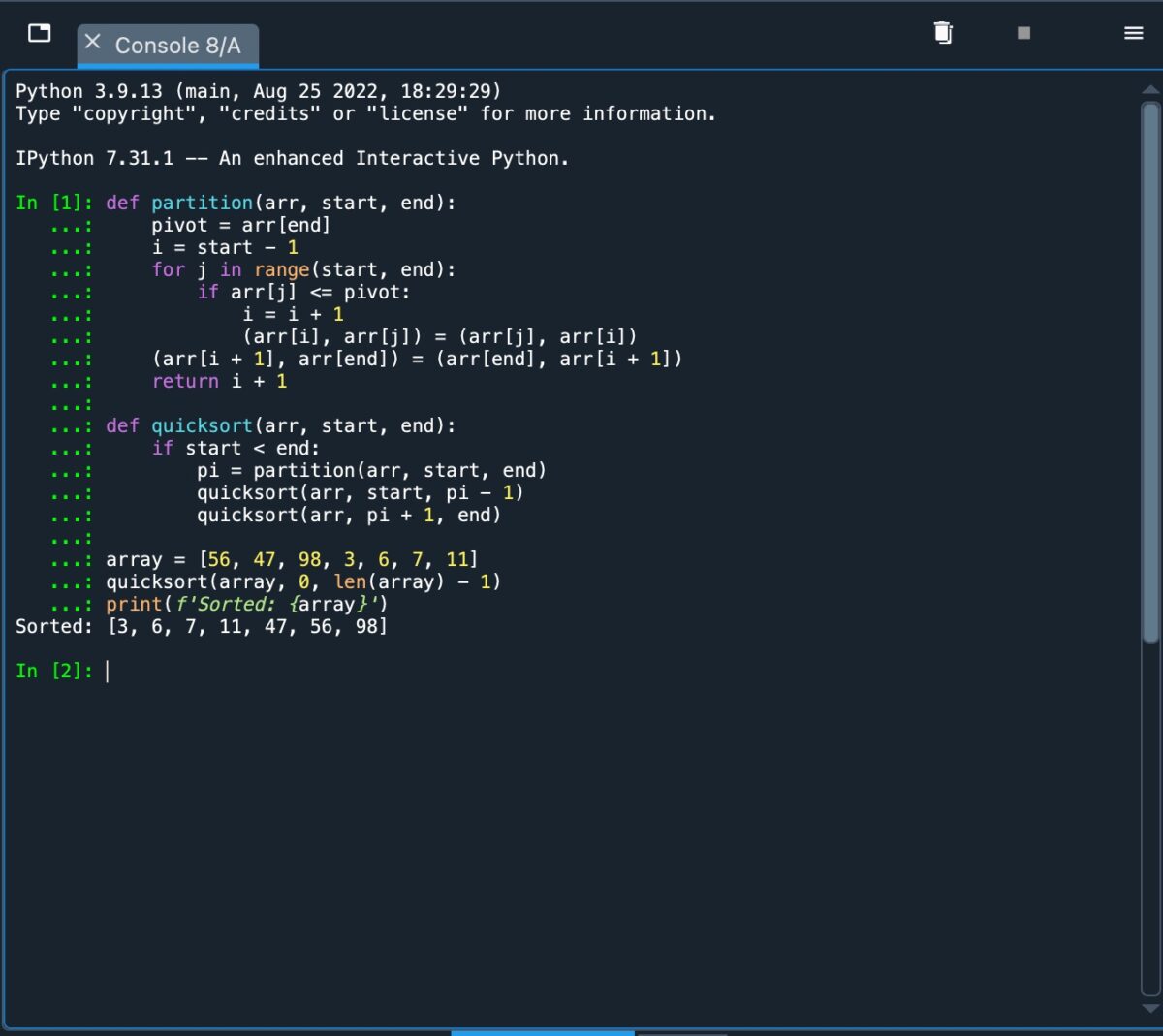
ตอนนี้เราได้กล่าวถึงพื้นฐานเบื้องหลังการเรียงลำดับอย่างรวดเร็วแล้ว เรามาปรับใช้โดยใช้ Python รหัสที่เราใช้สามารถอธิบายได้ดังนี้:
def partition(arr, start, end): pivot=arr[end] i=start-1 for j in range(start, end): if arr[j]=pivot: i=i + 1 (arr[i], arr[j]=(arr[j], arr[i]) (arr[i + 1], arr[end])=(arr[จบ], arr[i + 1]) คืนค่า i + 1 def quicksort(arr, start, end): ถ้า start end: pi=พาร์ติชั่น(arr, start, end) quicksort(arr, start, pi-1) quicksort(arr, pi + 1, end) array=[56, 47, 98, 3, 6, 7, 11] quicksort(array, 0, len(array)-1) print(f’Sorted: {array}’)
อันดับแรก เรากำลังกำหนดฟังก์ชันพาร์ติชันเป็นฟังก์ชันของอาร์เรย์ โดยมีดัชนีเริ่มต้นและสิ้นสุด
จากนั้นค่า Pivot จะถูกตั้งค่าเป็นองค์ประกอบสุดท้ายของอาร์เรย์ และ i จะเริ่มต้นเป็นจุดเริ่มต้น ดัชนี ลบ 1
ลูป”for”วนซ้ำอาร์เรย์ จากดัชนีเริ่มต้นไปยังดัชนีสิ้นสุด ลบ 1
คำสั่ง”if”สลับองค์ประกอบปัจจุบัน j มีค่าที่ดัชนี i ถ้า j น้อยกว่าหรือเท่ากับ ตรงกับเดือย จากนั้นตัวแปร i จะเพิ่มขึ้น
หลังจากนี้ จุดเปลี่ยนจะถูกสลับกับองค์ประกอบที่ดัชนี i+1 ซึ่งหมายความว่าองค์ประกอบทั้งหมดทางซ้ายของเดือยมีค่าน้อยกว่าหรือเท่ากับมัน และองค์ประกอบทางขวามีค่ามากกว่ามัน
ดัชนีของค่าเดือยจะถูกส่งกลับ
จากนั้น”Quicksort”จะถูกกำหนดให้เป็นฟังก์ชันของอาร์เรย์ และอาร์เรย์จะได้รับการตรวจสอบเพื่อให้แน่ใจว่ามีองค์ประกอบมากกว่าหนึ่งรายการ
จากนั้นจึงเรียกใช้ฟังก์ชัน”พาร์ติชัน”โดยมีดัชนี ค่าที่กำหนดเป็น”pi”Quick sort เรียกว่าการวนซ้ำในแถบย่อยด้านซ้ายและด้านขวา จนกว่าแต่ละแถบย่อยจะมีเพียงองค์ประกอบเดียว
ในที่สุด อาร์เรย์ที่เรียงลำดับจะถูกสร้างขึ้น และพิมพ์ออกมาโดยใช้ฟังก์ชัน”พิมพ์”
 การเรียงลำดับด่วนเรียกว่าเรียกซ้ำทางด้านซ้าย และแถบย่อยด้านขวา จนกว่าแต่ละแถบย่อยจะมีเพียงองค์ประกอบเดียว
การเรียงลำดับด่วนเรียกว่าเรียกซ้ำทางด้านซ้าย และแถบย่อยด้านขวา จนกว่าแต่ละแถบย่อยจะมีเพียงองค์ประกอบเดียว
©”TNGD”.com
กรณีการใช้งาน Quick Sort ที่ดีที่สุดและแย่ที่สุด
ในขณะที่ทฤษฎีที่อยู่เบื้องหลังการจัดเรียงอย่างรวดเร็วอาจ ดูเหมือนจะซับซ้อนในตอนแรก อัลกอริทึมมีข้อดีมากมายและโดยทั่วไปค่อนข้างรวดเร็ว มาดูความซับซ้อนของเวลาและพื้นที่ของการจัดเรียงอย่างรวดเร็ว
ความซับซ้อนของเวลาของการจัดเรียงอย่างรวดเร็ว
ตารางสรุปความซับซ้อนของเวลาของการจัดเรียงอย่างรวดเร็ว
<ตาราง > CaseTime ComplexityBestO (n log n)AverageO (n log n)WorstO (n2)
กรณีที่ดีที่สุดคือเมื่อพาร์ติชันมีความสมดุล โดยที่ pivot ใกล้เคียงหรือเท่ากับค่ามัธยฐาน ดังนั้น แถบย่อยทั้งสองจะมีขนาดใกล้เคียงกัน และมีการดำเนินการ n ครั้งในแต่ละระดับ ซึ่งนำไปสู่ความซับซ้อนของเวลาแบบลอการิทึม
เมื่อองค์ประกอบจุดหมุนค่อนข้างใกล้ นี่เป็นกรณีเฉลี่ย ความซับซ้อนของเวลาจะเหมือนกับกรณีที่ดีที่สุดเนื่องจากอาร์เรย์มีขนาดพอๆ กันโดยประมาณ
อย่างไรก็ตาม กรณีที่เลวร้ายที่สุดจะเปลี่ยนความซับซ้อนของเวลาเป็นเวลากำลังสอง นี่เป็นเพราะอาร์เรย์ไม่สมดุลอย่างมาก โดยที่เดือยอยู่ใกล้กับองค์ประกอบต่ำสุดหรือสูงสุด สิ่งนี้ทำให้เกิดสถานการณ์ที่ subarrays มีขนาดไม่เท่ากัน โดยหนึ่งอันมีองค์ประกอบเพียงองค์ประกอบเดียว ด้วยเหตุนี้ จึงมีการเรียกซ้ำ n ระดับและการดำเนินการ n รายการ ซึ่งนำไปสู่การพึ่งพากำลังสองกับขนาดอินพุต
ความซับซ้อนของพื้นที่ของการจัดเรียงแบบด่วน
ปัจจัยอีกประการหนึ่งที่ต้องพิจารณาคือพื้นที่ ความซับซ้อนของการเรียงลำดับอย่างรวดเร็ว สรุปได้ดังนี้:
ความซับซ้อนของพื้นที่สำหรับการเรียงลำดับอย่างรวดเร็วจะเหมือนกันสำหรับสิ่งที่ดีที่สุดและค่าเฉลี่ย กรณี นี่เป็นเพราะอัลกอริทึมมีล็อก n ระดับการเรียกซ้ำ และการเรียกซ้ำแต่ละครั้งใช้พื้นที่หน่วยความจำในจำนวนที่คงที่ ดังนั้น พื้นที่หน่วยความจำทั้งหมดจะเป็นสัดส่วนกับความลึกของแผนผังการเรียกซ้ำ
อย่างไรก็ตาม ในกรณีที่เลวร้ายที่สุด ความซับซ้อนของพื้นที่จะถูกเปลี่ยนเป็น O(n) เนื่องจากแผนผังการเรียกซ้ำไม่สมดุลอย่างมาก หมายความว่ามีการเรียกซ้ำ n ครั้ง
สรุปผล
โดยรวมแล้ว การเรียงลำดับแบบด่วนเป็นวิธีที่มีประสิทธิภาพมากในการเรียงลำดับตามชื่อ อาร์เรย์โดยเฉพาะขนาดใหญ่ เมื่อเข้าใจกระบวนการแล้ว การนำไปใช้และแก้ไขก็ค่อนข้างง่าย มีประโยชน์ในสถานการณ์ที่หลากหลายและเป็นรากฐานที่ดีสำหรับอัลกอริทึมการเรียงลำดับที่ซับซ้อนมากขึ้น
ถัดไป…
การเรียงลำดับด่วนคืออะไรและทำงานอย่างไร (พร้อมตัวอย่าง) คำถามที่พบบ่อย (คำถามที่พบบ่อย)
การจัดเรียงอย่างรวดเร็วคืออะไร
การจัดเรียงอย่างรวดเร็วเป็นอัลกอริทึมการจัดเรียงสำหรับการจัดเรียงอาร์เรย์ของข้อมูล ทำงานโดยการเลือกองค์ประกอบเดือยและแบ่งอาร์เรย์ออกเป็นสองอาร์เรย์ย่อย หนึ่งมีองค์ประกอบที่เล็กกว่าเดือยและอีกองค์ประกอบหนึ่งมีองค์ประกอบที่ใหญ่กว่า กระบวนการนี้จะเกิดขึ้นซ้ำๆ จนกว่าแต่ละ subarray จะถูกจัดเรียงและมีเพียงองค์ประกอบเดียว จากนั้นอาร์เรย์จะรวมกันเพื่อให้เป็นอาร์เรย์ที่เรียงลำดับ
การจัดเรียงอย่างรวดเร็วเป็นอัลกอริทึมที่เสถียรหรือไม่
การจัดเรียงอย่างรวดเร็วมักเป็นอัลกอริทึมที่ไม่เสถียร ซึ่งหมายความว่าลำดับสัมพัทธ์ขององค์ประกอบที่เท่ากันอาจไม่ถูกรักษาไว้ในผลลัพธ์สุดท้าย
คุณจะเลือกองค์ประกอบ Pivot ด้วยการจัดเรียงอย่างรวดเร็วได้อย่างไร
คุณสามารถเลือกองค์ประกอบแรกหรือองค์ประกอบสุดท้าย หรือเลือกแบบสุ่มก็ได้ ด้วยชุดข้อมูลที่มีขนาดใหญ่เป็นพิเศษ การสุ่มตัวเลือกมักจะนำไปสู่ประสิทธิภาพที่ดี
ความซับซ้อนของเวลาของการจัดเรียงอย่างรวดเร็วคืออะไร
กรณีที่ดีที่สุดและค่าเฉลี่ย คือ O(n log n) ในขณะที่กรณีที่แย่ที่สุดคือ O(n2)
การจัดเรียงด่วนมีความซับซ้อนของพื้นที่เท่าใด
สิ่งที่ดีที่สุด และกรณีเฉลี่ยคือ O(log n) ในขณะที่กรณีเลวร้ายที่สุดคือ O(n)
กรณีใดดีที่สุดสำหรับการใช้การจัดเรียงอย่างรวดเร็ว
Quick sort สามารถใช้กับอาร์เรย์ได้หลายประเภท แต่บางครั้ง ทางเลือกอื่นๆ เช่น การเรียงลำดับแบบฮีปหรือการเรียงลำดับแบบผสานอาจทำงานได้ดีกว่า เนื่องจากข้อจำกัดบางประการ โดยปกติแล้วคุณต้องมีอัลกอริทึมที่เสถียร เช่น การเรียงลำดับการผสาน หรือเวลาที่เป็นปัจจัยสำคัญ ตัวอย่างเช่น ความซับซ้อนของเวลากรณีที่เลวร้ายที่สุดของการจัดเรียงแบบฮีปนั้นดีพอๆ กับความซับซ้อนของเวลากรณีโดยเฉลี่ยสำหรับการเรียงลำดับอย่างรวดเร็ว อัลกอริทึมที่ง่ายกว่า เช่น การเลือกหรือการเรียงลำดับการแทรกอาจเร็วกว่าสำหรับชุดข้อมูลขนาดเล็กด้วย