© metamorworks/Shutterstock.com
เมื่อจัดเรียงอาร์เรย์ของข้อมูล สิ่งสำคัญคือต้องทำความคุ้นเคยกับอัลกอริทึมการเรียงลำดับ ในโครงสร้างข้อมูล การเรียงลำดับเป็นการจัดเรียงข้อมูลในรูปแบบเฉพาะตามความสัมพันธ์เชิงเส้นระหว่างรายการข้อมูล
การเรียงลำดับมีความสำคัญเนื่องจากสามารถเพิ่มประสิทธิภาพการค้นหาข้อมูลในระดับที่สูงมากเมื่อข้อมูลถูกจัดเรียงในรูปแบบที่กำหนด นอกจากนี้ การเรียงลำดับสามารถแสดงข้อมูลในรูปแบบที่อ่านง่ายขึ้น เรามีอัลกอริธึมการเรียงลำดับที่หลากหลาย แต่ในบทความนี้ เราจะตรวจสอบว่าการจัดเรียงแบบฮีปคืออะไร และใช้งานอย่างไร มาเริ่มกันเลย!

Heap Sort คืออะไร: คำนิยามที่แน่นอน
Heap sort เป็นอัลกอริทึมการเรียงลำดับที่เป็นที่รู้จักและมีประสิทธิภาพ เป็นแนวคิดที่ใช้ในการจัดเรียงข้อมูลอาร์เรย์โดยการกำจัดองค์ประกอบทีละรายการจากฮีปซึ่งเป็นส่วนทรีไบนารีที่สมบูรณ์ของรายการ จากนั้นจึงแทรกข้อมูลเหล่านั้นลงในส่วนที่เรียงลำดับของรายการ
การจัดเรียงฮีปโดยพื้นฐานแล้ว มีสองขั้นตอนที่เกี่ยวข้อง:
การสร้างฮีป ไม่ว่าจะเป็นฮีปสูงสุดหรือฮีปขั้นต่ำโดยใช้องค์ประกอบของอาร์เรย์ที่ระบุ การลบองค์ประกอบรูทของฮีปที่สร้างขึ้นในเฟสแรกซ้ำๆ
อัลกอริทึมการจัดเรียงแบบฮีปทำงานอย่างไร
นี่คือวิธีการใช้อัลกอริทึมการจัดเรียงแบบฮีป:
สร้างฮีปสูงสุดเพื่อเก็บข้อมูลจากรายการที่ไม่เรียงลำดับ นำค่าที่ใหญ่ที่สุดออกจาก ฮีปและใส่ลงในรายการที่เรียงลำดับ สลับรูทของฮีปกับองค์ประกอบสุดท้ายในรายการ จากนั้นปรับสมดุลฮีปอีกครั้ง เมื่อฮีปสูงสุดว่างเปล่า ให้ส่งคืนรายการที่เรียงลำดับ
นี่คืออัลกอริทึม
HeapSort(arr)
CreateMaxHeap(arr)
for i=length(arr) เป็น 2
สลับ arr[1] กับ arr[i]
heap_size[arr]=heap_size[arr] ? 1
MaxHeapify(arr,1)
จบ
มาตรวจสอบขั้นตอนกันอีกหน่อย
ขั้นตอนที่ 1: สร้างค่าสูงสุด-heap
CreateMaxHeap(arr)
heap_size(arr)=length(arr)
สำหรับ i=length(arr)/2 ถึง 1
MaxHeapify(arr,i)
End
ในอัลกอริทึมนี้ เราจะต้องสร้าง max-heap อย่างที่เราทราบกันดีว่าใน max-heap ค่าที่ใหญ่ที่สุดคือค่ารูท แต่ละโหนดพาเรนต์ต้องมีค่ามากกว่าโหนดย่อยที่เกี่ยวข้อง
ลองนึกดูว่าเรามีรายการค่าที่ไม่เรียงลำดับด้านล่าง:
[14, 11, 2, 20, 3, 10 , 3]
โดยการวางค่าของเราลงในโครงสร้างข้อมูลแบบ max-heap รายการของเราจะมีลักษณะดังนี้:
[20, 11, 14, 2, 10, 5 , 3]
เราสามารถนำเสนอ max-heap ข้างต้นได้ดังนี้:
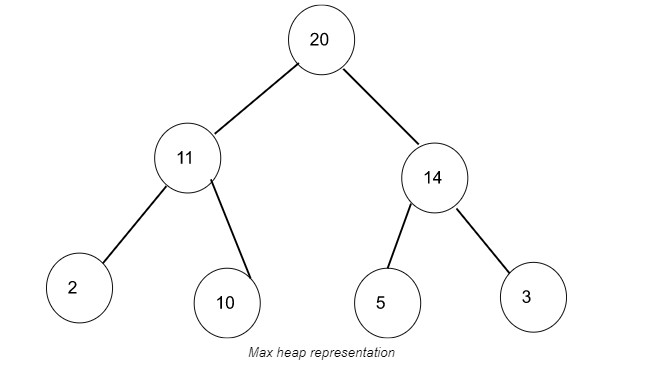 การนำเสนอ max-heap.
การนำเสนอ max-heap.
©”TNGD”.com
ขั้นตอนที่ 2: นำรากของ heap ออก
ในการจัดเรียงข้อมูล เราจะแยกและกำจัดค่าที่ใหญ่ที่สุดออกจากฮีปซ้ำๆ จนกว่าจะว่างเปล่า หากเราปฏิบัติตามหลักการของฮีป เราสามารถคาดการณ์ได้ว่าค่าที่ใหญ่ที่สุดจะอยู่ที่รูทของฮีป
หลังจากกำจัดค่าที่ใหญ่ที่สุดแล้ว เราไม่สามารถละทิ้งฮีปโดยไม่รูทได้ เพราะมัน จะส่งผลให้สองโหนดถูกตัดการเชื่อมต่อ เราสามารถแลกเปลี่ยนโหนดรูทกับองค์ประกอบสุดท้ายในฮีปแทนได้ เนื่องจากองค์ประกอบสุดท้ายไม่มีลูก จึงสามารถลบออกจากฮีปได้อย่างง่ายดาย
อย่างไรก็ตาม ขั้นตอนนี้ทำให้เกิดปัญหาใหญ่ ด้วยการสลับองค์ประกอบทั้งสอง ตอนนี้รูตโหนดไม่ได้ใหญ่ที่สุดในฮีป ฮีปจะต้องได้รับการปรับโครงสร้างใหม่เพื่อให้แน่ใจว่ามีความสมดุล
ขั้นตอนที่ 3: ฮีปลง (กู้คืนฮีป)
ค่ารูทไม่ใช่ค่าที่มากกว่า หลักการฮีปคือ ถูกละเมิดเนื่องจากผู้ปกครองต้องมีค่ามากกว่าคุณค่าของเด็ก
อย่างไรก็ตาม ปัญหานี้มีวิธีแก้ไข! เราจะต้องทำให้เป็นกอง ซึ่งเกี่ยวข้องกับการเพิ่มค่าที่ส่วนท้ายของกอง และดำเนินการตามโครงสร้างข้อมูลของคุณจนกว่าคุณจะพบตำแหน่งที่เหมาะสม หากต้องการลดจำนวนลง คุณต้องเปรียบเทียบค่ารูทใหม่กับลูกของมัน เลือกลูกที่มีค่ามากกว่า และสลับกับค่ารูท ค่อยๆ ลงกองจนกว่าจะสมดุล
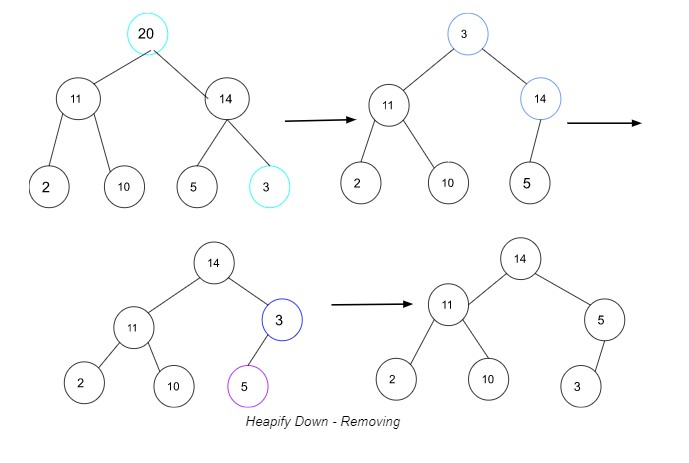 ภาพประกอบของกระบวนการ heapify down
ภาพประกอบของกระบวนการ heapify down
©”TNGD”.com
ในตัวอย่างด้านบน คุณสลับค่ารูทเดิม 20 กับ 3 ซึ่งเป็นค่ารองด้านขวาสุด มี 3 เป็นรูทใหม่ ให้เปรียบเทียบค่ากับค่าลูก 14 และเนื่องจากมีค่ามากกว่า 3 ให้สลับค่าเพื่อให้ 14 เป็นรูทใหม่ ถัดไป เปรียบเทียบ 3 กับลูกใหม่ 5 และเนื่องจาก 5 มากกว่า 3 ให้สลับเพื่อให้ 5 เป็นค่าพาเรนต์ใหม่ เนื่องจากไม่มีลูกอื่นให้เปรียบเทียบกับ 3 ฮีปจึงมีความสมดุลแล้ว
ขั้นตอนที่ 4: ทำซ้ำ
คุณจะต้องทำซ้ำขั้นตอนการเปลี่ยนรูทและสุดท้าย นำค่าที่ใหญ่ที่สุดออก และปรับสมดุลของฮีปใหม่ ตราบใดที่โครงสร้างข้อมูลมีขนาดมากกว่า 1 เมื่อตรงตามเงื่อนไขนี้ คุณจะมีชุดของค่าที่เรียงลำดับ
ความซับซ้อนของการเรียงลำดับฮีป
ความซับซ้อนของเวลา
นี่คือความซับซ้อนของเวลาของการจัดเรียงแบบฮีปในกรณีที่ดีที่สุด กรณีเฉลี่ย และกรณีที่เลวร้ายที่สุด
<ตาราง >กรณีความซับซ้อนของเวลากรณีที่ดีที่สุดO(n log n)กรณีเฉลี่ยO(n log n)กรณีเลวร้ายที่สุดO (n log n)
Best Case Complexity: เกิดขึ้นเมื่ออาร์เรย์ถูกจัดเรียงแล้ว นั่นคือไม่จำเป็นต้องเรียงลำดับ O(n log n) คือเวลาที่ซับซ้อนที่สุดของการจัดเรียงแบบฮีปความซับซ้อนของกรณีเฉลี่ย: เกิดขึ้นเมื่อองค์ประกอบในอาร์เรย์ไม่ได้ถูกจัดเรียงจากน้อยไปมากหรือมากไปน้อยอย่างเหมาะสม ส่งผลให้ คำสั่งที่สับสน O(n log n) คือเวลาเฉลี่ยของความซับซ้อนของกรณีและปัญหาของการจัดเรียงแบบฮีป ความซับซ้อนของกรณีที่เลวร้ายที่สุด: สิ่งนี้จะเกิดขึ้นเมื่อคุณต้องการเรียงลำดับองค์ประกอบอาร์เรย์ในลำดับย้อนกลับ หมายความว่าหากองค์ประกอบเริ่มต้นจากมากไปน้อย คุณจะต้องเรียงลำดับจากน้อยไปหามาก O(n log n) คือเวลาที่ซับซ้อนที่สุดของการจัดเรียงแบบฮีป
ความซับซ้อนของพื้นที่
ความซับซ้อนของพื้นที่ของการจัดเรียงฮีปคือ O(1)
<ตาราง >ความซับซ้อนของพื้นที่O(1)คงที่N0
อัลกอริทึมการจัดเรียงแบบฮีปถูกนำไปใช้อย่างไร?
นี่คือวิธีการจัดเรียงแบบฮีปในภาษาการเขียนโปรแกรม Java
//การจัดเรียงทรีย่อยให้เป็นฮีป ในที่นี้ “i” คือดัชนีรูทโหนดใน arr[] และ “x” คือขนาดฮีป
public class HeapSort {
public static void sort(int[] arr) {
int x=arr.length;
//จัดเรียงอาร์เรย์ใหม่ (สร้างฮีป)
สำหรับ (int i=x/2 – 1; i >=0; i–)
heapify(arr, x, i);
//แยกองค์ประกอบออกจากฮีปทีละรายการ
สำหรับ (int i=x – 1; i > 0; i–) {
//เลื่อนรูทเริ่มต้นไปที่จุดสิ้นสุด
int temp=arr[0];
arr[0]=arr[i];
arr[i]=temp;
//เรียกใช้ฟังก์ชัน heapify สูงสุดบนฮีปที่ลดลง
heapify(arr, i, 0);
}
}
static void heapify(int[] arr, int x, int i) {
int ใหญ่ที่สุด=i;//เริ่มต้นค่าที่ใหญ่ที่สุดเป็นรูท
int l=2 * i + 1;//ซ้าย
int r=2 * i + 2;//ขวา
//ถ้าชายด์ซ้ายใหญ่กว่าราก
if (l x && arr[l] > arr[ที่ใหญ่ที่สุด])
ที่ใหญ่ที่สุด=l;
//ถ้าลูกที่ถูกต้องใหญ่กว่าลูกที่ใหญ่ที่สุดจนถึงตอนนี้
if (r x && arr[r] > arr[ใหญ่ที่สุด])
ใหญ่ที่สุด=r;
//ถ้าใหญ่ที่สุดไม่ใช่ราก
if (ใหญ่ที่สุด !=i){
int swap=arr[i];
arr[i]=arr[ใหญ่ที่สุด];
arr[ใหญ่ที่สุด]=สลับ;
//สร้างกลุ่มย่อยที่ได้รับผลกระทบซ้ำๆ
heapify(arr, x, ใหญ่ที่สุด);
}
}
//a ฟังก์ชันพิมพ์อาร์เรย์ขนาด x
โมฆะคงที่ printArray(int[]) {
int x=arr.length;
สำหรับ (int i=0; i x; ++i)
System.out.print(arr[i] + ” “);
System.out.println();
}
//รหัสไดรเวอร์
public static void main (String[] args) {
int[] arr={ 13, 12, 14, 6, 7, 8 };
sort(arr);
System.out.println(“อาร์เรย์ที่เรียงลำดับคือ”);
printArray(arr);
}
}
Output
นี่คืออาร์เรย์จำนวนเต็มที่เรียงลำดับจากน้อยไปหามาก
อาร์เรย์ที่เรียงลำดับคือ
6, 7, 8, 12, 13, 14
ข้อดีและข้อเสียของอัลกอริทึมการจัดเรียงแบบฮีป
ข้อดี
ประสิทธิภาพ: อัลกอริทึมการเรียงลำดับนี้มีประสิทธิภาพมากเนื่องจากเวลาที่ต้องใช้ในการจัดเรียงฮีปเพิ่มขึ้นตามลอการิทึม ในขณะที่อัลกอริทึมอื่นๆ เวลาจะช้าลงแบบทวีคูณเมื่อรายการการเรียงลำดับเพิ่มขึ้นความเรียบง่าย >: เมื่อเทียบกับอัลกอริทึมอื่นๆ ที่มีประสิทธิภาพเท่ากัน มันง่ายกว่าเนื่องจากไม่ได้ใช้หลักการวิทยาการคอมพิวเตอร์ขั้นสูง เช่น การเรียกซ้ำ การใช้หน่วยความจำ: การจัดเรียงแบบฮีปใช้หน่วยความจำขั้นต่ำในการเก็บรายการเริ่มต้นของรายการที่จะจัดเรียง และไม่จำเป็นต้องใช้พื้นที่หน่วยความจำเพิ่มเติมในการทำงาน
ข้อเสีย
แพง: การจัดเรียงแบบฮีปมีค่าใช้จ่ายสูง ไม่เสถียร: การจัดเรียงแบบฮีปไม่น่าเชื่อถือเนื่องจากอาจจัดเรียงลำดับองค์ประกอบที่เกี่ยวข้องใหม่ไม่มีประสิทธิภาพ: เมื่อต้องจัดการกับข้อมูลที่มีความซับซ้อนสูง การจัดเรียงแบบฮีปจะไม่มีประสิทธิภาพมากนัก
การประยุกต์ใช้การจัดเรียงแบบกองซ้อน
คุณอาจเคยพบอัลกอริทึมของ Dijkstra ซึ่งใช้การจัดเรียงแบบกองเพื่อกำหนดเส้นทางที่สั้นที่สุด ในโครงสร้างข้อมูล การจัดเรียงแบบฮีปช่วยให้ดึงค่าที่เล็กที่สุด (สั้นที่สุด) หรือใหญ่ที่สุด (ยาวที่สุด) ได้อย่างรวดเร็ว มีแอปพลิเคชันที่หลากหลาย รวมถึงการกำหนดลำดับในสถิติ การจัดการคิวลำดับความสำคัญในอัลกอริทึมของ Prim (หรือที่เรียกว่าแผนผังสแปนนิงขั้นต่ำ) และดำเนินการเข้ารหัส Huffman หรือบีบอัดข้อมูล
ในทำนองเดียวกัน ระบบปฏิบัติการต่างๆ ก็ใช้ Heap อัลกอริทึมการเรียงลำดับสำหรับงานและการจัดการกระบวนการ เนื่องจากเป็นไปตามคิวลำดับความสำคัญ
ในสถานการณ์จริง การเรียงลำดับแบบฮีปสามารถนำไปใช้กับร้านซิมการ์ด ซึ่งมีลูกค้าต่อคิวยาวเหยียด รอให้บริการ ลูกค้าที่ต้องจ่ายบิลสามารถจัดลำดับความสำคัญได้ เนื่องจากงานของพวกเขาใช้เวลาน้อยที่สุด วิธีการนี้จะช่วยประหยัดเวลาสำหรับลูกค้าจำนวนมากและหลีกเลี่ยงความล่าช้าที่ไม่จำเป็น ซึ่งนำไปสู่ประสบการณ์ที่มีประสิทธิภาพและน่าพึงพอใจสำหรับทุกคน
บทสรุป
อัลกอริทึมการเรียงลำดับหรือการค้นหาทุกรายการมีข้อดีและข้อเสีย และการจัดเรียงแบบกองก็ไม่มีข้อยกเว้น อย่างไรก็ตาม ข้อเสียของ Heap Sort นั้นค่อนข้างน้อย ตัวอย่างเช่น ไม่ต้องการพื้นที่หน่วยความจำเพิ่มเติมนอกเหนือจากที่จัดสรรไว้แล้ว
เวลาเป็นอีกปัจจัยหนึ่ง พบว่าความซับซ้อนของเวลาถูกกำหนดโดยใช้ nlog(n) แต่การเรียงลำดับฮีปจริงน้อยกว่า O(nlog(n)) เนื่องจากการแยกจากการจัดเรียงแบบฮีปจะลดขนาด จึงใช้เวลาน้อยลงเมื่อกระบวนการดำเนินต่อไป ดังนั้น Heap Sort จึงได้รับการยกย่องอย่างกว้างขวางว่าเป็นหนึ่งในอัลกอริธึมการเรียงลำดับที่”ดีที่สุด”ในขอบเขตของโครงสร้างข้อมูลด้วยเหตุผลหลายประการ
Heap Sort คืออะไร และคุณใช้อย่างไร คำถามที่พบบ่อย (คำถามที่พบบ่อย)
Heapify หมายความว่าอย่างไร
Heapify คือกระบวนการสร้างโครงสร้างข้อมูลฮีปจากการแสดงอาร์เรย์ของไบนารี ต้นไม้. กระบวนการนี้สามารถใช้เพื่อสร้าง Max-Heap หรือ Min-Heap เริ่มต้นจากดัชนีสุดท้ายของโหนด non-leaf ในไบนารีทรี ซึ่งดัชนีถูกกำหนดโดย n/2 – 1 Heapify ใช้งานโดยใช้การเรียกซ้ำ
Heap Sort ทำงานอย่างไร
Heap sort เป็นอัลกอริทึมการเรียงลำดับตามการเปรียบเทียบ มันทำงานโดยการย้ายองค์ประกอบที่ใหญ่ที่สุดจากพื้นที่ที่ไม่ได้เรียงลำดับไปยังพื้นที่ที่เรียงลำดับ ซึ่งจะทำให้พื้นที่ที่ไม่ได้เรียงลำดับมีขนาดเล็กลง การจัดเรียงแบบฮีปแสดงภาพองค์ประกอบของอาร์เรย์เป็นฮีป และเป็นที่รู้จักกันว่ามีเวลาทำงานที่เหมาะสมที่สุด อัลกอริทึมนี้มีประโยชน์เมื่อคุณต้องการรักษาลำดับในขณะที่แยกองค์ประกอบขั้นต่ำหรือสูงสุดออกจากอาร์เรย์
คุณจะ”จัดกลุ่ม”ต้นไม้ได้อย่างไร
หากต้องการปรับรูปร่างหรือสร้างไบนารีทรีจำนวนมาก คุณต้องเริ่มด้วยการเลือกโหนดเป็นรูทโหนดของทรีย่อย จากนั้น คุณเปรียบเทียบค่าของรูทโหนดกับค่าของโหนดลูกด้านซ้ายและด้านขวา ถ้าโหนดลูกมีค่าที่ใหญ่กว่า (ในกรณีของฮีปสูงสุด) หรือน้อยกว่า (ในกรณีของฮีปขั้นต่ำ) มากกว่าโหนดรูท ให้คุณสลับค่าของโหนดรูทและโหนดลูกด้วย ค่าที่มากกว่า (หรือน้อยกว่า) หลังจากสลับค่าแล้ว คุณจะวนซ้ำทรีย่อยที่รูทที่โหนดย่อยจนกว่าทรีย่อยทั้งหมดจะตรงตามคุณสมบัติฮีป คุณทำขั้นตอนนี้ซ้ำสำหรับทุกโหนดในทรีจนกว่าทรีทั้งหมดจะตรงตามคุณสมบัติฮีป
ความซับซ้อนของเวลาของการฮีปคือ O(log n) โดยที่ n คือจำนวนโหนดในทรีย่อยที่ถูกฮีป.
ไบนารีฮีปคืออะไร
ไบนารีฮีปเป็นโครงสร้างข้อมูลที่สามารถพิจารณาได้ว่าเป็นไบนารีทรีที่สมบูรณ์ โดยที่โหนดพาเรนต์ทุกโหนด น้อยกว่าหรือเท่ากับลูกของมัน (ในกองขั้นต่ำ) หรือมากกว่าหรือเท่ากับลูกของมัน (ในกองสูงสุด)
ข้อดีของการจัดเรียงแบบกองคืออะไร
ข้อดีของการเรียงลำดับแบบฮีป ได้แก่ ความซับซ้อนของเวลา O(n log n) ซึ่งเร็วกว่าอัลกอริทึมการเรียงลำดับยอดนิยมอื่นๆ เช่น การเรียงลำดับแบบฟองและการเรียงลำดับแบบแทรก นอกจากนี้ การจัดเรียงแบบฮีปยังมีหน่วยความจำเหลือน้อย เนื่องจากต้องใช้พื้นที่เพิ่มเติมในปริมาณคงที่เท่านั้น
ข้อเสียของการจัดเรียงแบบฮีปคืออะไร
ข้อเสียของการจัดเรียงแบบฮีปรวมถึงคุณสมบัติการเรียงลำดับที่ไม่เสถียร ซึ่งหมายความว่าลำดับสัมพัทธ์ขององค์ประกอบที่เท่ากันอาจไม่ถูกรักษาไว้หลังจากการเรียงลำดับ นอกจากนี้ การจัดเรียงแบบฮีปยังไม่ค่อยมีประสิทธิภาพสำหรับอาร์เรย์ขนาดเล็ก และลักษณะการเรียกซ้ำอาจทำให้ประสิทธิภาพการทำงานช้าลงในบางสถาปัตยกรรม